[数据结构]KMP算法(含next数组详解）

字符串匹配问题

给定一个字符串 s 和一个要匹配的模式串 p。模式串 p 有可能在 s 中多次出现，请求出模式串 p 在 s 中所有出现的起始位置。

暴力匹配算法 BF

算法思路

在面对字符串匹配问题时，很容易想到暴力求解。字符串匹配的暴力算法思路很简单，即在 s 中枚举起点 i，对于每个起点匹配字符串 p。

大致步骤为:

(1) 枚举起点i，定义一个状态值flag = true 以及 k = i，j = 0；

(2) 如果 s[k] == p[j]，就继续k++, j++; 如果 s[k] != p[j]，就将flag置flase，并break；

(3) 对于每个起点 i ，如果flag = true，就输出位置 i 。

暴力算法代码

这里输入字符串下标从1开始，与后文相统一。

#include<iostream>
#include<cstdio>
using namespace std;

static const int N = 1000010, M = 100010;
char s[N], p[M];
int slen, plen;
int ne[N];

int main(){
    cin >> plen >> p + 1 >> slen >> s + 1;
    for(int i = 1; i <= slen - plen + 1; i++){
        bool flag = true;
        for(int j = 1, k = i; j <= plen; j++, k++){
            if(s[k] != p[j]){
                flag = false;
                break;
            }
        }
        if(flag) printf("%d ", i);
    }
}

---

KMP算法

KMP算法的含义

KMP算法是一种改进的字符串匹配算法，是由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，所以简称KMP算法。其算法核心是在匹配失败后利用next数组记录的信息来一定程度上减少匹配次数，以此提高字符串匹配的效率。

KMP算法涉及的基本概念

（1）s 为模板字符串；

（2）p 为模式串，即需要在 s 中匹配的字符串；

（3）公共前后缀：假定一个字符串的长度为len且下标从1开始，若字符串中范围[1, i]和范围[j, len]完全匹配，则称这两段为此字符串的公共前后缀；

（4）next 数组：next 数组是KMP算法的核心，next[i] 记录的是模式串 p 中前 i 长度范围内的最长公共前后缀长度，后文会做详解。KMP算法在进行字符串匹配时若出现失配，模式串 p 可以根据 next 数组记录的信息进行等价的后移。

（5）两大核心步骤：

1、求解 next 数组

2、进行字符串匹配

注意字符串的下标从 1 开始，并且在匹配过程中每次将 s[i] 和 p[i + 1] 进行比较。

KMP算法的匹配思路

KMP算法匹配核心图解

红色虚线所标注的范围内为当前已经匹配的部分，红色空心圆圈为当前比较的两个字符。

KMP算法匹配举例及图解

（1）

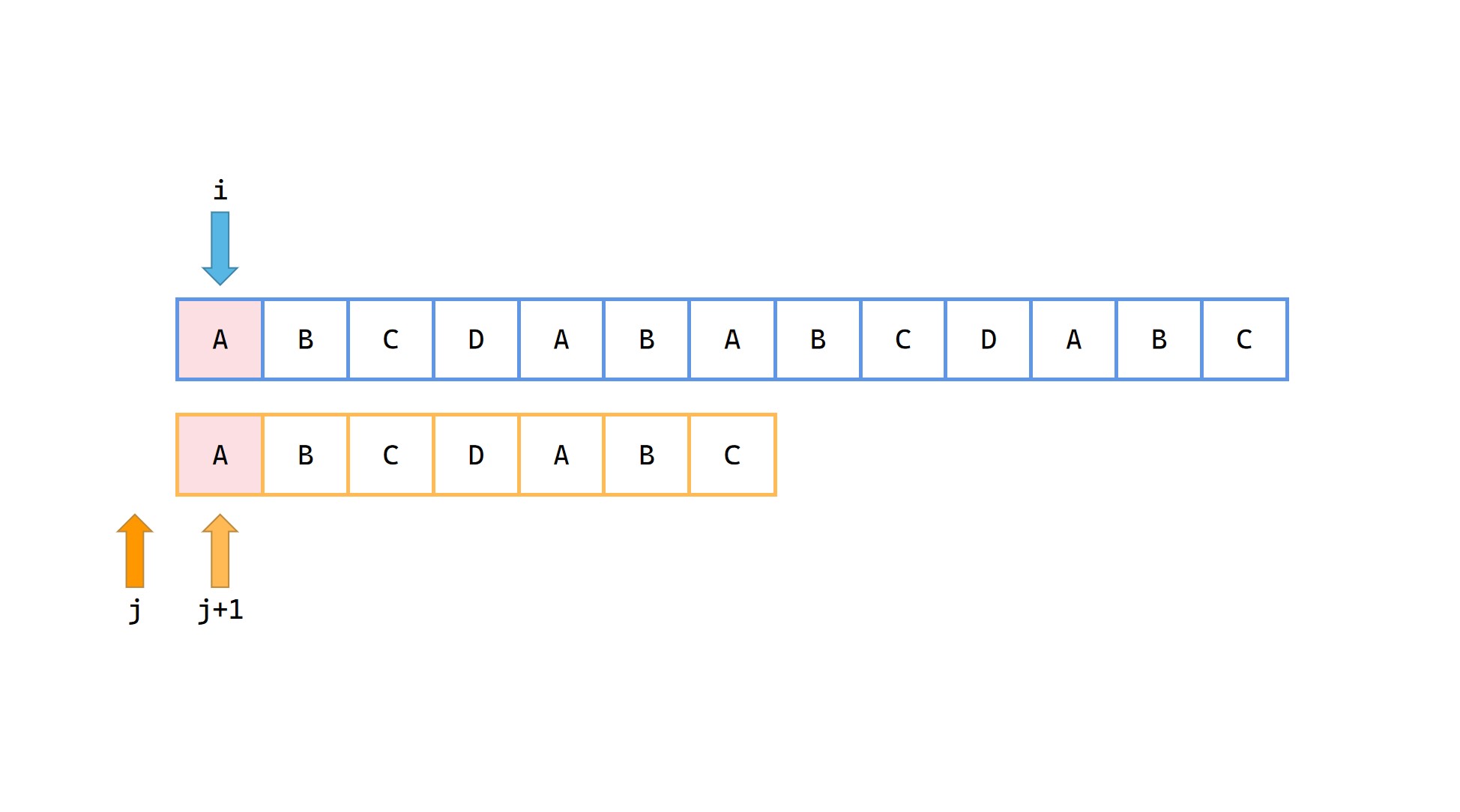
（2）

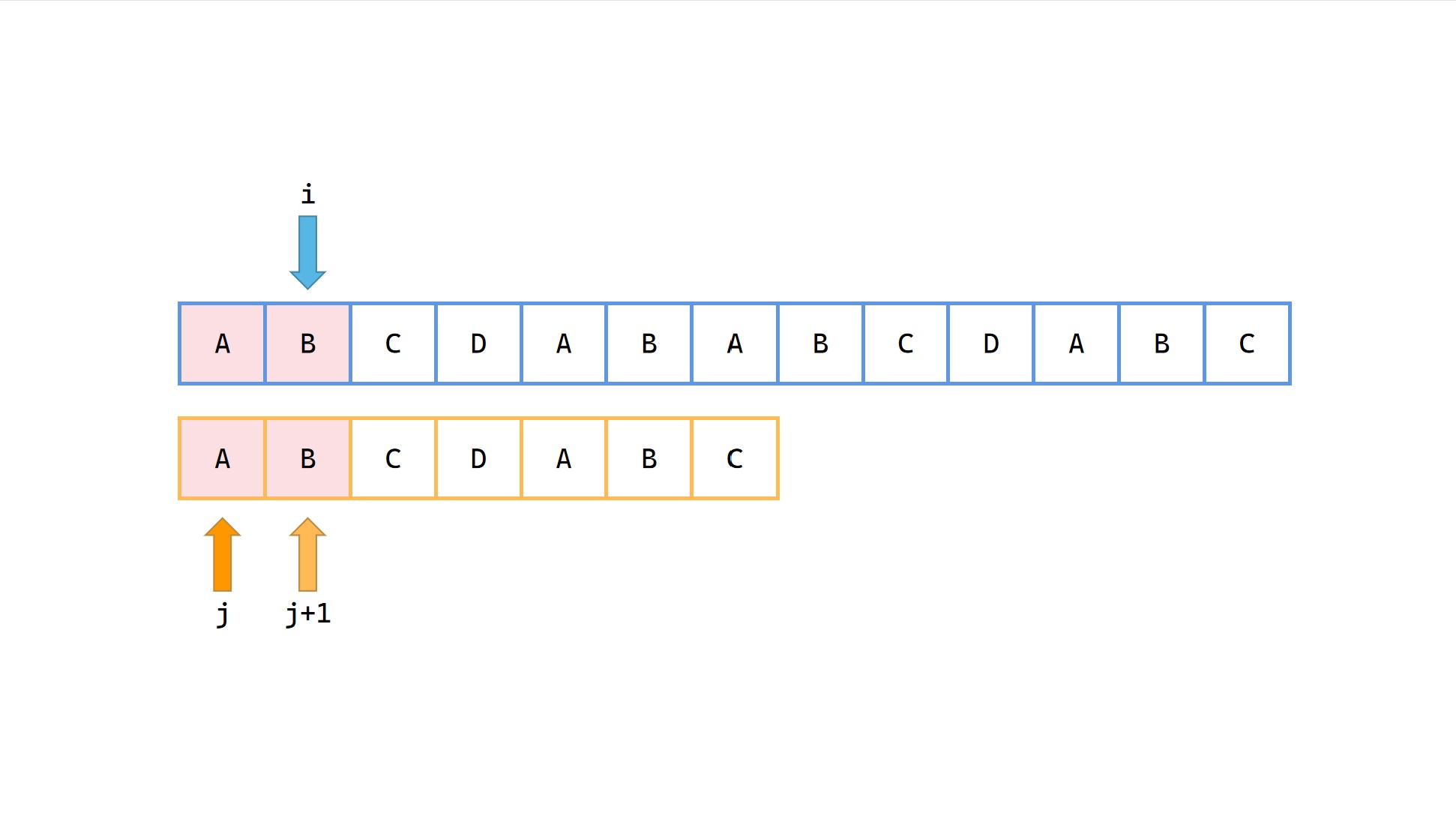
（3）

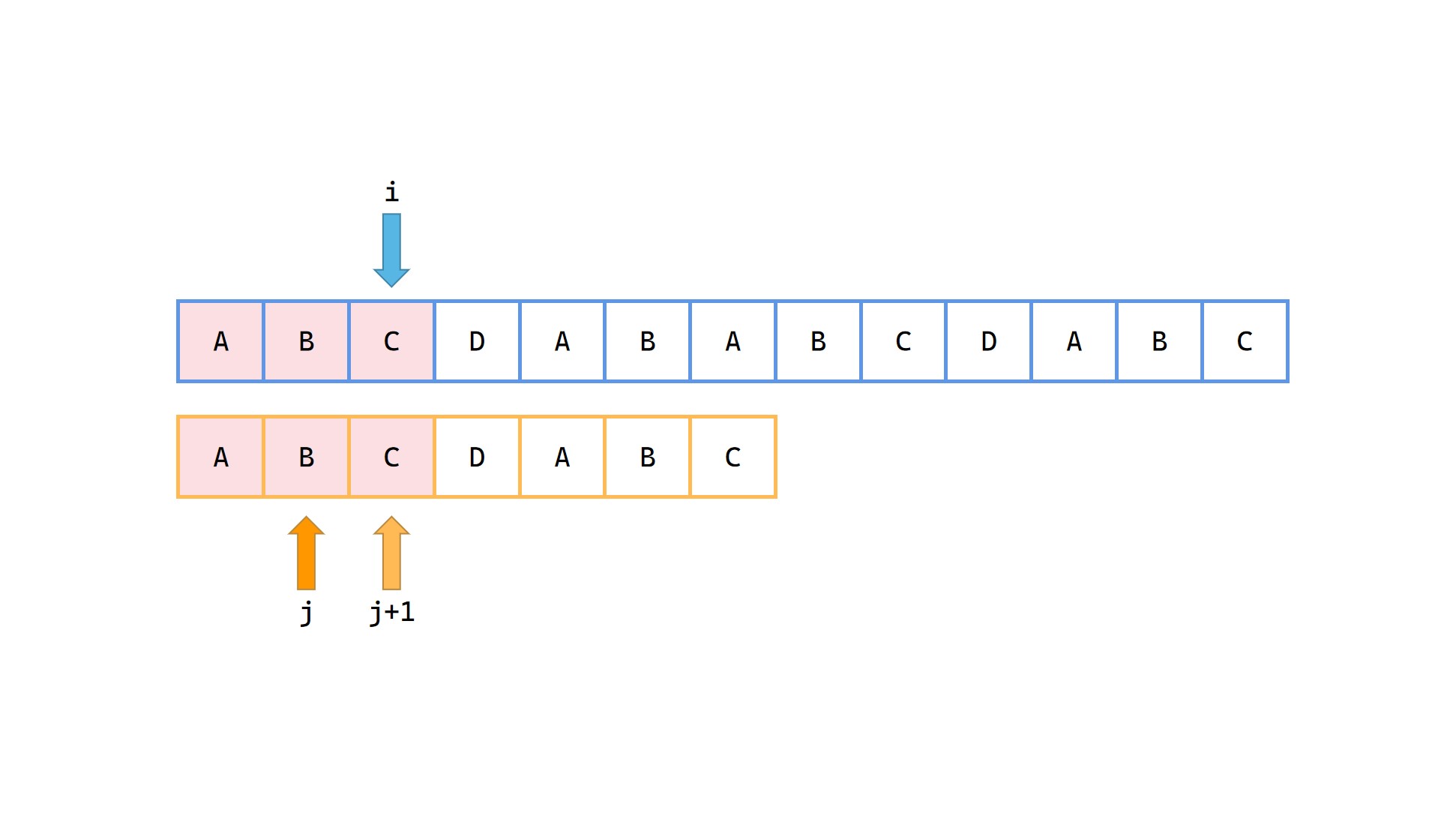
（4）

（5）

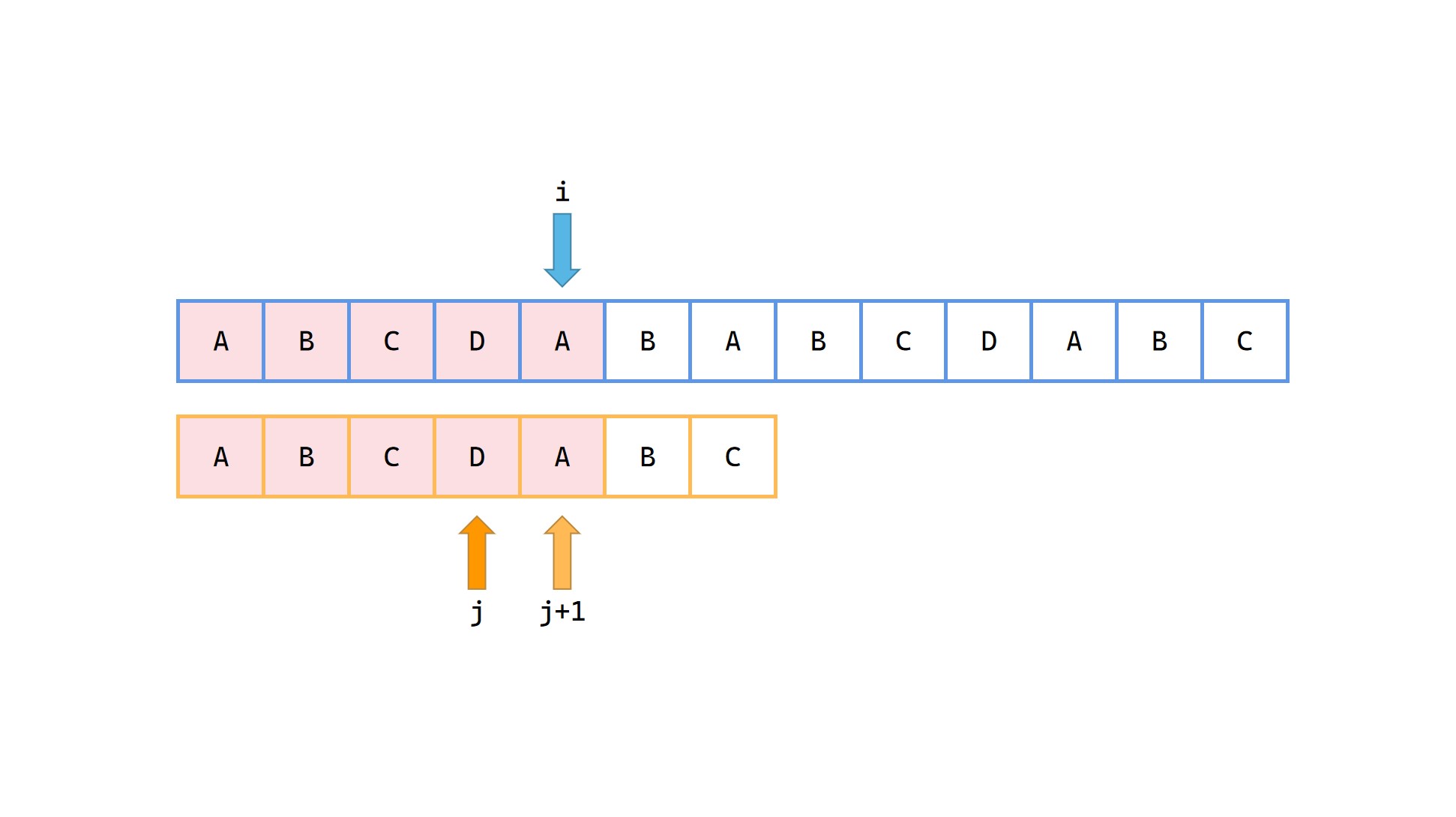
（6）

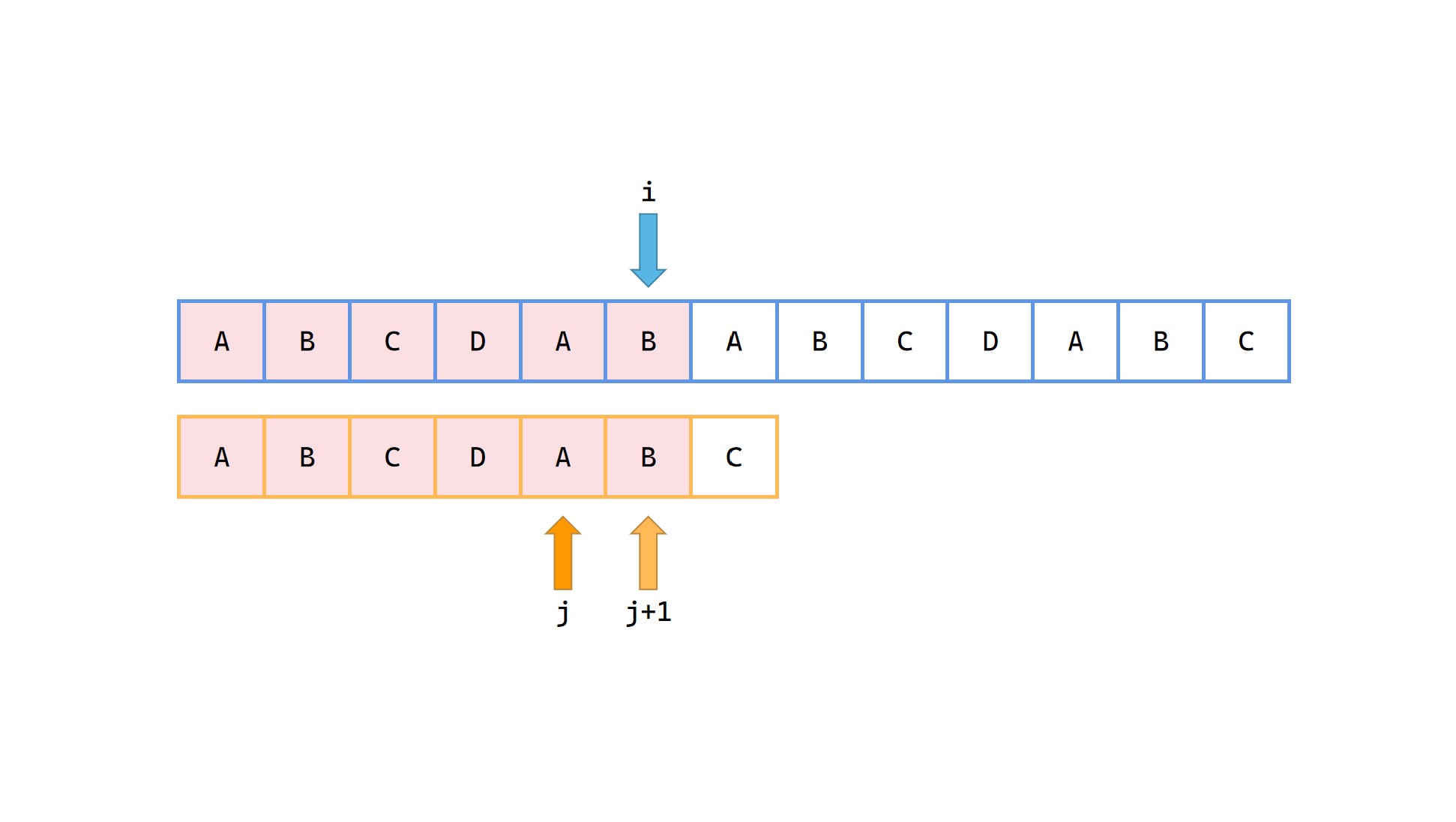
（7）

此时出现了失配，需要将j = next[j]。

（8）

容易发现在 p 中前 6 长度的最长公共前后缀长度为2，j = next[6] = 2。

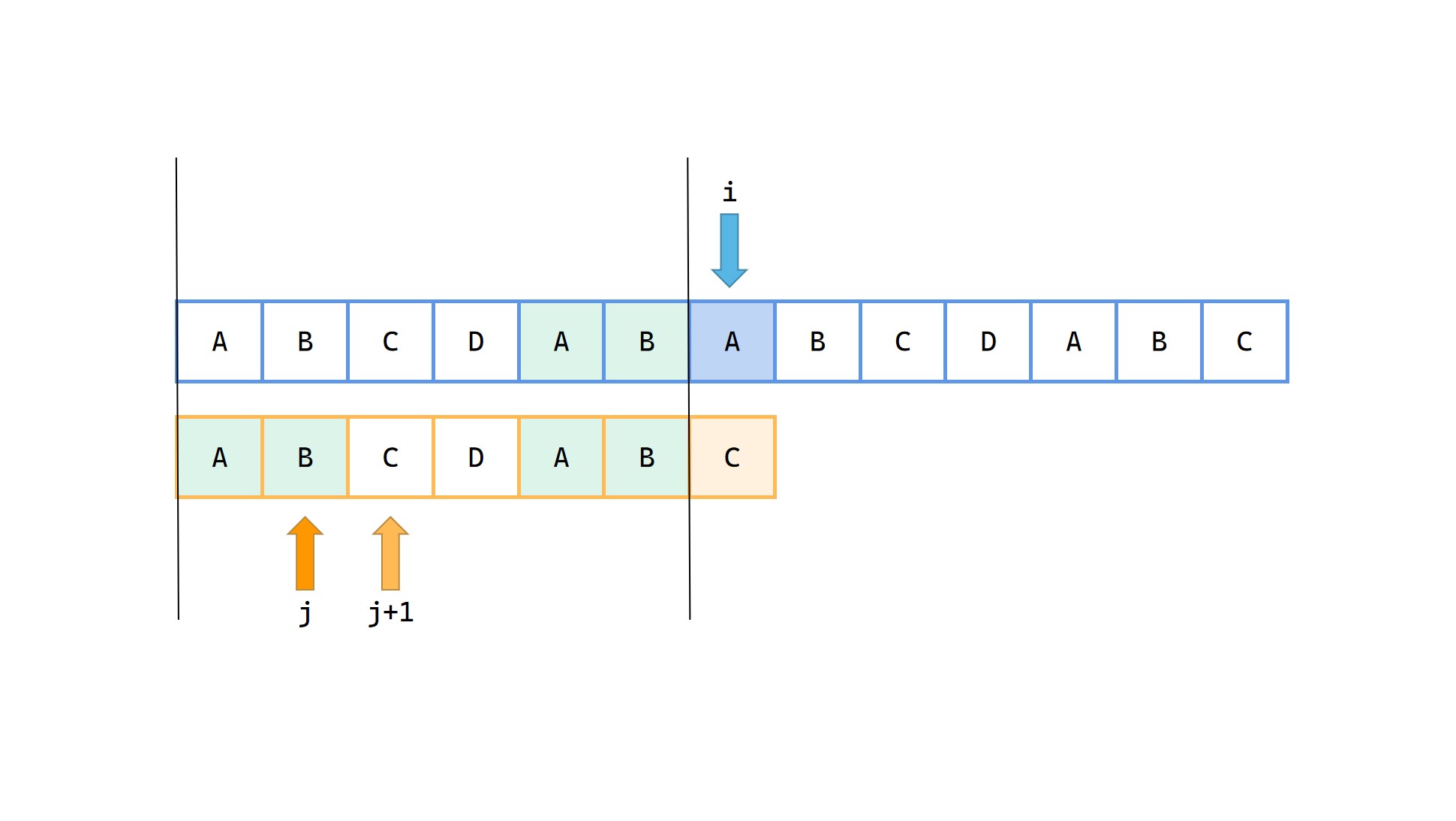
（9）

相当于模式串 p 整体向右移动了之前的 j - next[j] 的长度再开始匹配。

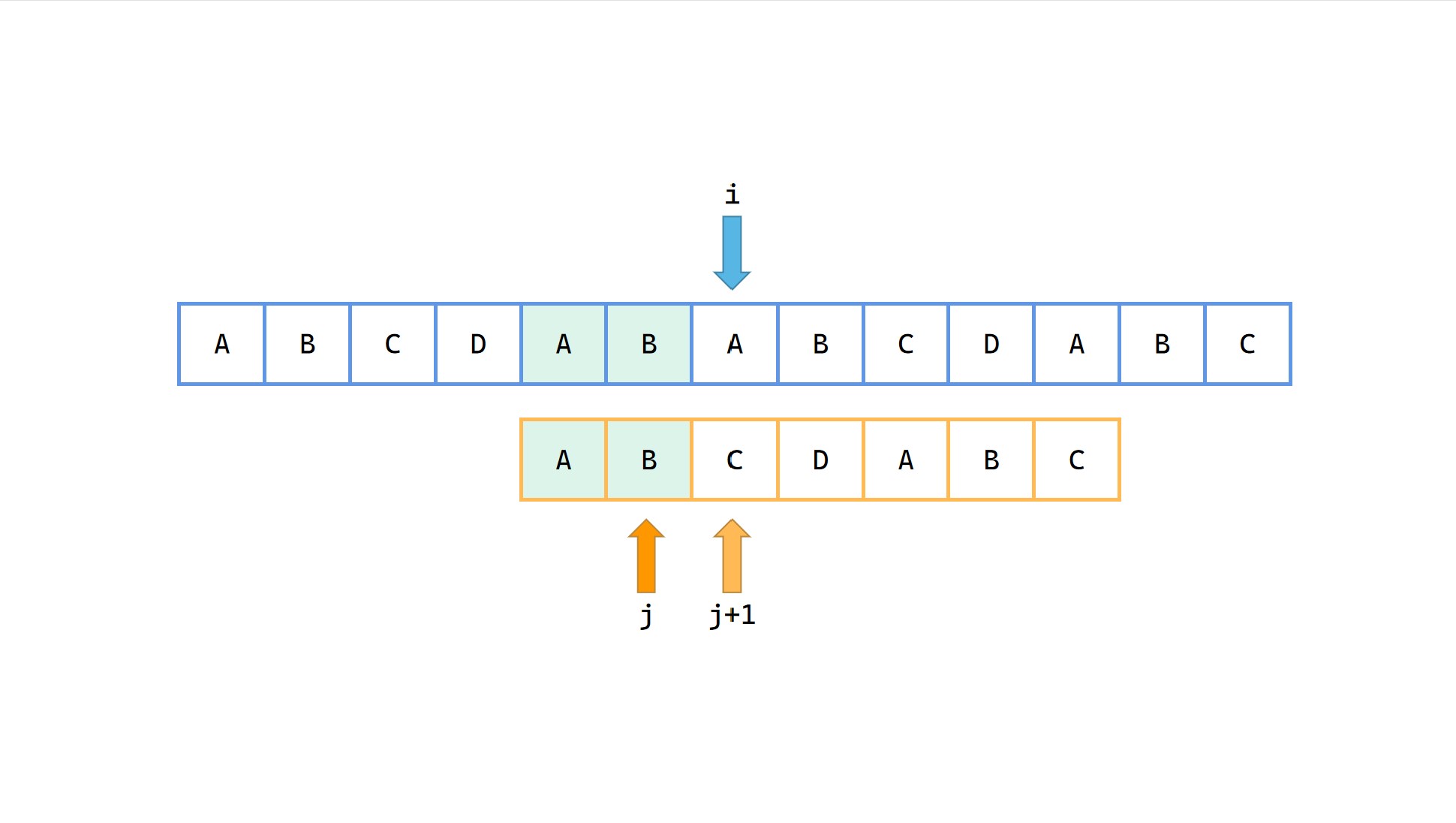
（10）

此时再次出现了失配，需要将 j = next[j]。

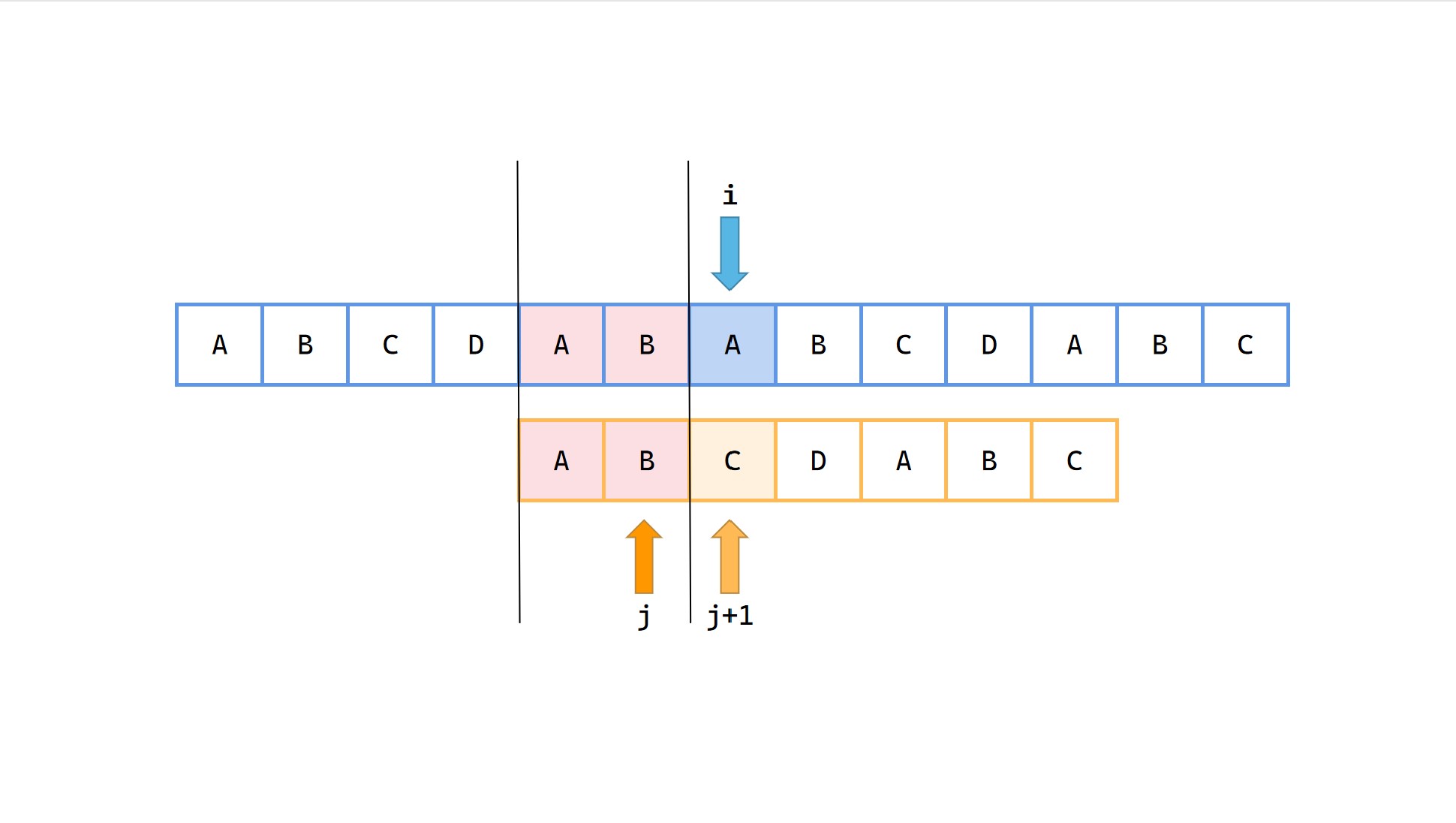
（11）

模式串 p 中前 2 长度的最长公共前后缀长度为0，j = next[2] = 0*。

（12）

相当于模式串 p 整体向右移动了之前的 j - next[j] 的长度再开始匹配。

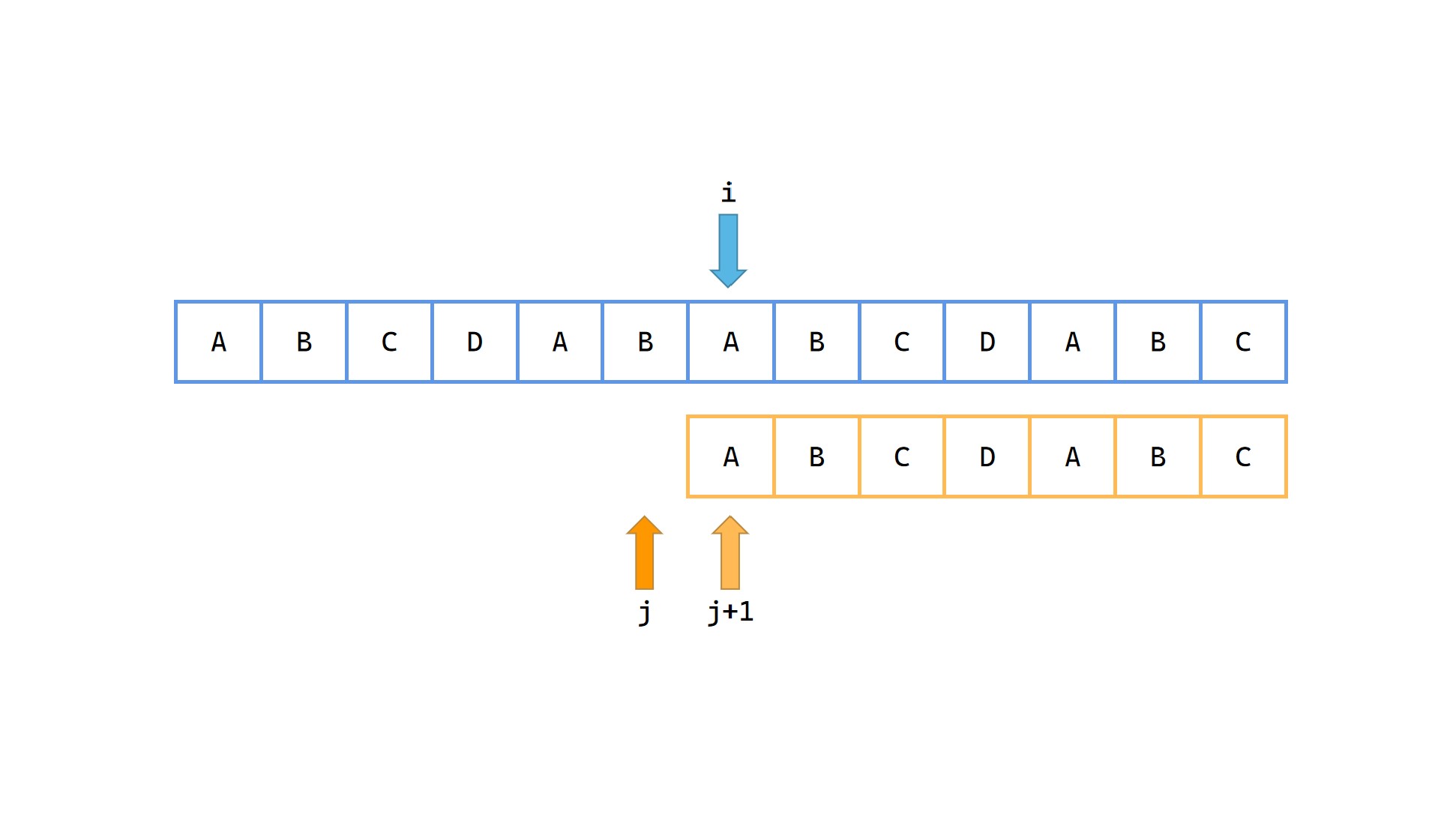
（13）

以当前 s[i] 这个字符为起点匹配模式串 p 成功。（前面省略了一些）

KMP算法匹配核心代码

    //匹配操作
    for(int i = 1, j = 0; i <= n; i++){
        //失配整体移动之后可能依旧失配，故用while
        while(j && s[i] != p[j + 1]) j = ne[j];
        //当前两个字符匹配
        if(s[i] == p[j + 1]) j++;
        if(j == m)  {
            printf("%d ", i - m + 1);  //返回匹配起始位置
            j = ne[j];     //可能存在多个位置匹配，继续匹配
        }
    }

---

next数组详解

next数组的含义及求解

next[i] 记录的是模式串 p 前 i 长度范围内最长公共前后缀的长度。例如字符串 ABDAB，可以发现此字符串前 4 长度的最长公共前后缀为 A，那么对于这个字符串，next[4] = 1；同理此字符串前 5 长度的最长公共前后缀为 AB，所以 next[5] = 2。

next 数组的求解和上文中字符串匹配的过程非常相近，相当于是自己与自己进行匹配。将其中一个 p依旧作为模式串，将另一个 p 视作字符串，并将其从下标2开始与模式串 p 进行匹配。

next数组核心图解

红色虚线所标注的范围内为当前已经匹配的部分，红色空心圆圈为当前比较的两个字符。

（1）求解next数组当前字符匹配

（2）求解next数组当前字符失配

next数组举例及图解

（1）

（2）

（3）

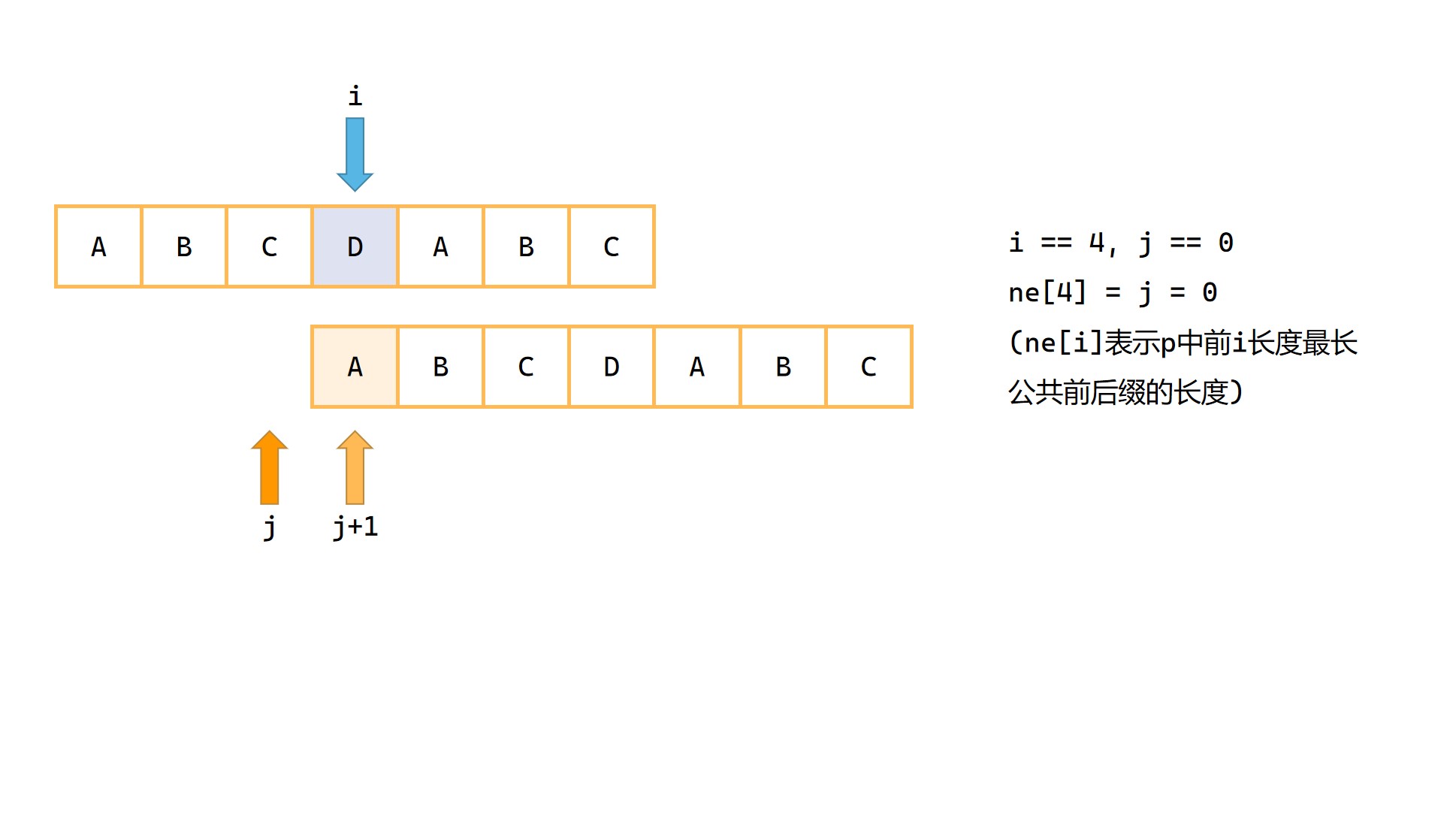
（4）

此时出现字符匹配

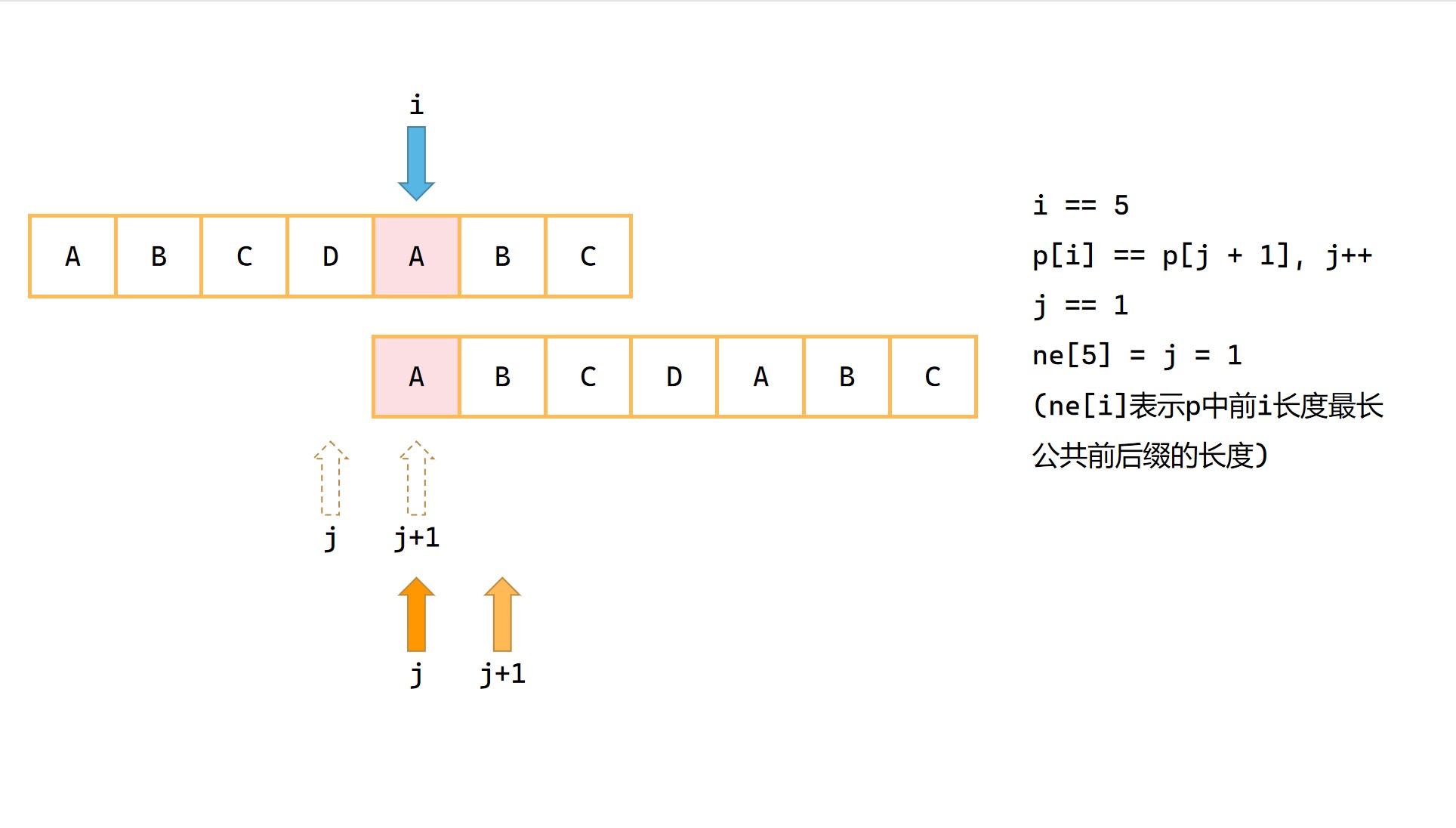
（5）

此时出现字符匹配

（6）

此时出现字符匹配

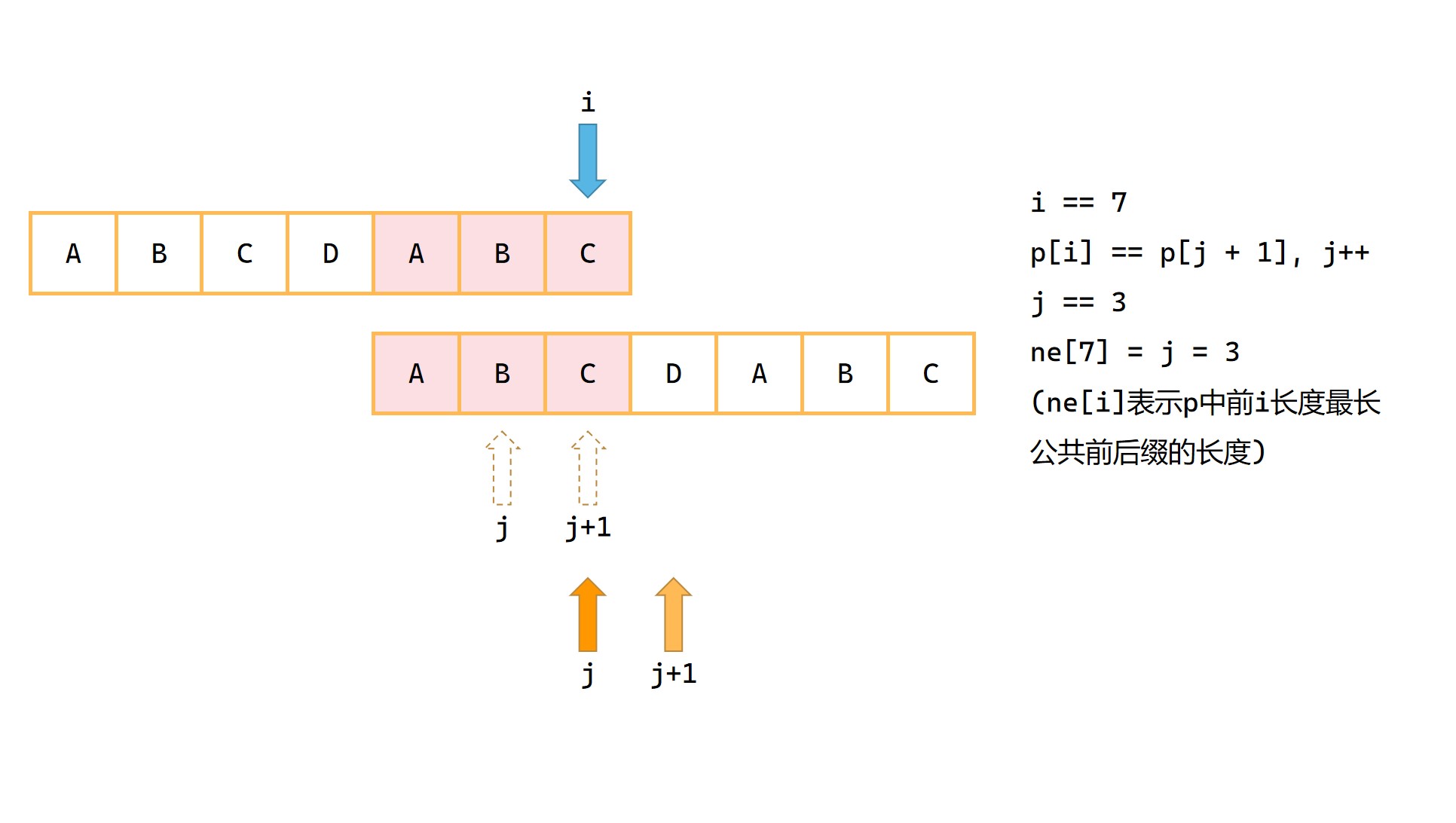
（7）

求解next数组完成

next数组核心代码

    //求next[]数组
    for(int i = 2, j = 0; i <= m; i++){
        //当前字符不匹配
        while(j && p[i] != p[j + 1]) j = ne[j];
        if(p[i] == p[j + 1]) j++;
        //记录前i长度最长公共前后缀长度j
        ne[i] = j;
    }

字符串下标以及next数组如此定义的原因

上文中字符串下标都从 1 开始，要实现也不难，C/C++从1开始输入即可，其他语言例如python，先插入一个字符即可。下标从 1 开始主要也是和next数组的定义有关。next数组记录的是模式串 p 中一定范围内的最长公共前后缀的长度，如果下标从0开始，这个KMP算法模板也可以进行，但是需要将next[0]置-1，而且求得的next数组有些违背本身的含义(变成记录的是前i下标最长公共前后缀长度-1)。

以下是下标从0开始的KMP算法模板:

int main(){
    cin >> m >> p >> n >> s;

    ne[0] = -1;
    for (int i = 1, j = -1; i < m; i ++ ){
        while (j >= 0 && p[j + 1] != p[i]) j = ne[j];
        if (p[j + 1] == p[i]) j ++ ;
        ne[i] = j;
    }

    for (int i = 0, j = -1; i < n; i ++ ){
        while (j != -1 && s[i] != p[j + 1]) j = ne[j];
        if (s[i] == p[j + 1]) j ++ ;
        if (j == m - 1){
            cout << i - j << ' ';
            j = ne[j];
        }
    }
    //输出next数组
    //cout<<endl<<"next[]: "<<endl;
    //for(int i = 0; i < m; i++) cout<<ne[i]<<' ';
}

以下是上述下标从0开始模板求得的next数组结果：



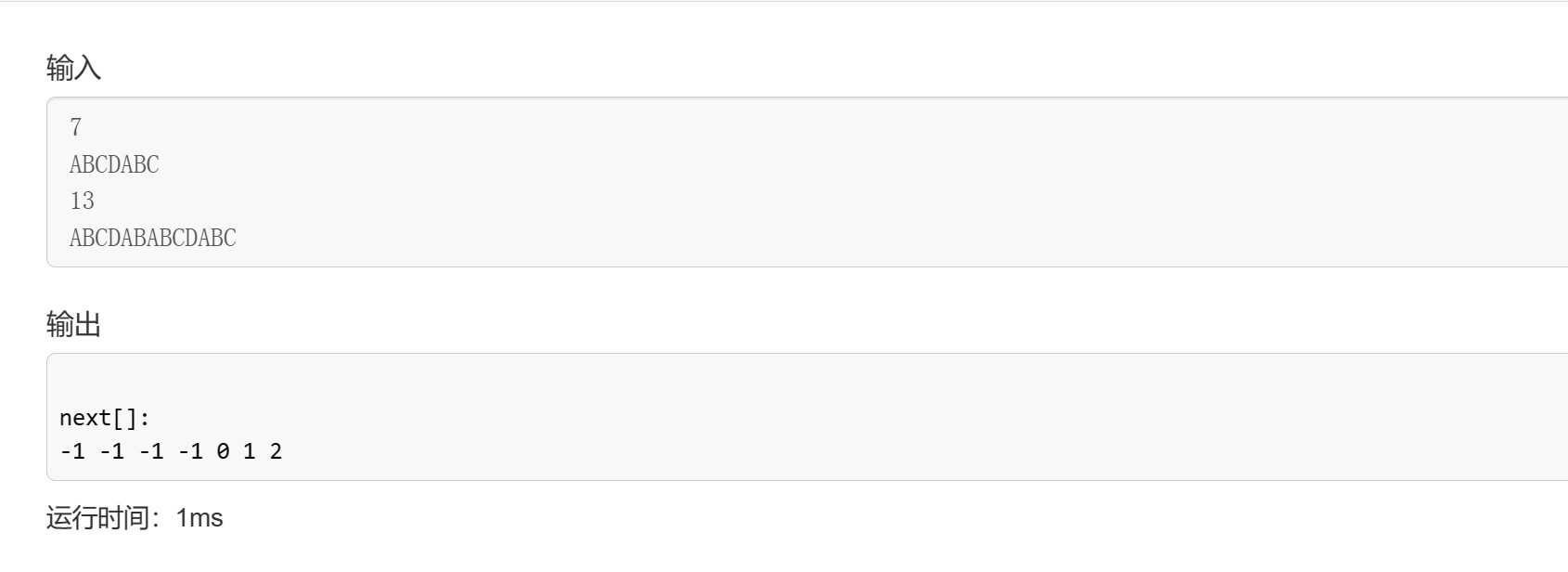
可以看出求得next数组记录的值恰好为前i下标最长公共前后缀长度-1。

---

完整程序

完整程序代码

#include<iostream>
using namespace std;

static const int N = 1000010, M = 100010;
char s[N], p[M];
int slen, plen;
int ne[N];

int main(){
    cin >> plen >> p + 1 >> slen >> s + 1;

    for(int i = 2, j = 0; i <= plen; i++){
        while(j && p[i] != p[j + 1]) j = ne[j];
        if(p[i] == p[j + 1]) j++;
        ne[i] = j;
    }

    for(int i = 1, j = 0; i <= slen; i++){
        while(j && s[i] != p[j + 1]) j = ne[j];
        if(s[i] == p[j + 1]) j++;
        if(j == plen){
            cout<<i - plen + 1<<' ';
            j = ne[j];
        }
    }
    //输出next数组
    //cout<<endl<<"next[]: "<<endl;
    //for(int i = 1; i <= plen; i++) cout<<ne[i]<<' ';
}

程序运行测试

---

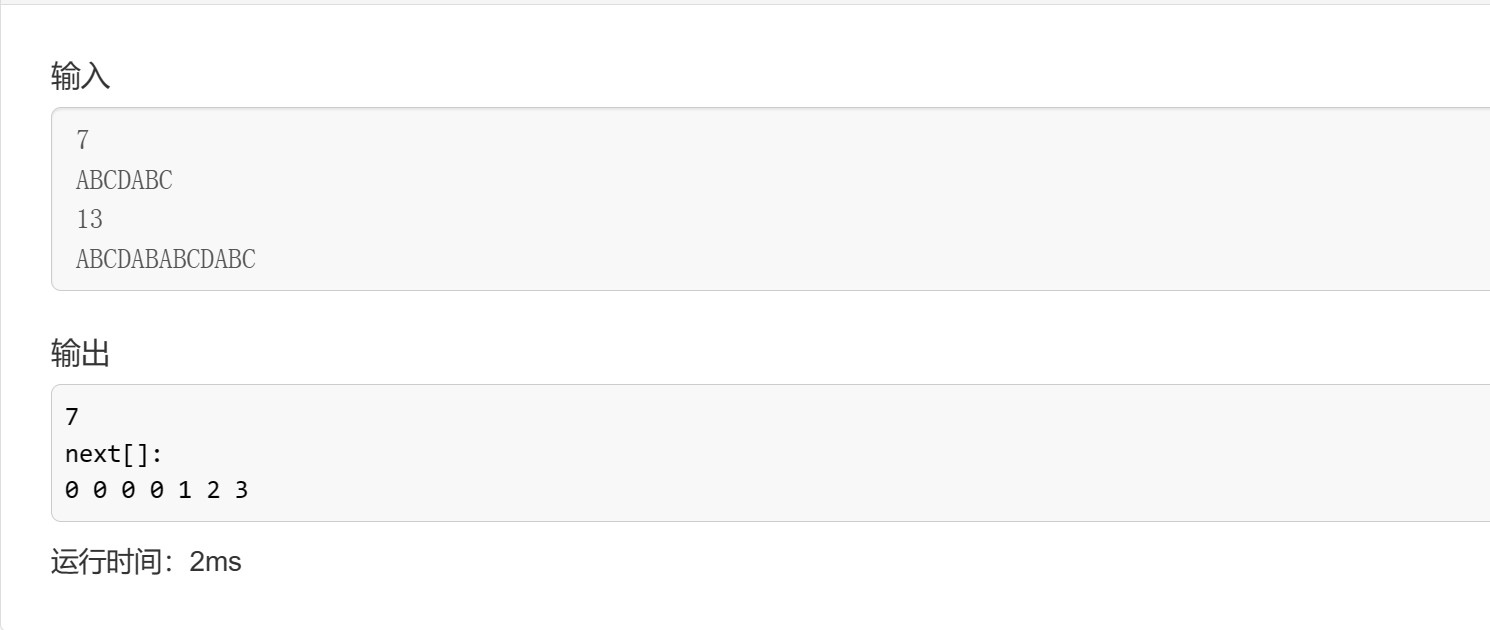
后记

网上大部分KMP的写法与我写的这篇随笔中不太相同，next数组的定义也不太一样。我所记录的是我自己认为最好理解的KMP算法的写法，没有任何贬低其他写法的意思喔，也许各有各的好处。