Arnold置乱

一、Arnold置乱概述

　　Arnold变换是俄国数学家弗拉基米尔·阿诺德（Vladimir Igorevich Arnold）提出，Arnold将其应用在遍历理论研究中。由于Arnold本人最初对一张猫的图片进行了此种变换，因此它又被称为猫脸变换（cat映射）。Cat映射可以把图像中各像素点的位置进行置换，使其达到加密的目的，多应用在多媒体混沌加密中。

　　Arnold置乱是一种数字图像处理技术，通过改变图像像素的排列顺序来产生视觉上的扭曲和变形效果。该技术主要应用于图像加密和保护，也可以用于生成艺术效果或增加图像的复杂度。

　　Arnold置乱的原理基于置换群的概念。对于一个n×n的图像，可以将其视为一个由n²个像素组成的向量。Arnold置乱通过一系列置换操作来改变这些向量的排列顺序，从而产生不同的视觉效果。

　　具体来说，Arnold置乱的操作是将每个像素坐标(x, y)进行置换操作，得到新的坐标(x', y')。置换操作的具体方法如下：

　　　　x' = (ax + y) mod n y' = (bx + (a*b+1)*y) mod n

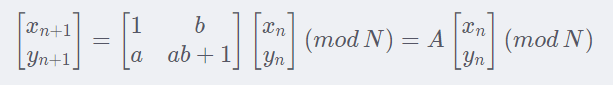
　　其中，a和b是两个置乱参数，n是图像大小。上述公式可以理解为将(x, y)映射到了一个新的坐标(x', y')。通过反复进行这样的置换操作，可以将图像像素的排列顺序进行混乱，从而产生视觉上的扭曲和变形效果。

　　值得注意的是，Arnold置乱是一种可逆操作，也就是说可以通过相反的操作将图像恢复为原始状态。具体来说，如果知道了置乱参数a和b以及进行置乱的迭代次数n，就可以对图像进行反向置乱操作，从而得到原始的图像。

　　在实际应用中，Arnold置乱常常被用于数字水印、图像加密等领域。通过对图像进行多次Arnold置乱操作，可以使得图像的像素排列变得非常复杂和随机，从而增加了图像的安全性和保密性。同时，Arnold置乱也可以用于生成艺术效果，例如在数字艺术中用于产生视觉上的扭曲和变形效果。

二、步骤

　　Arnold置乱的具体步骤如下：

1. 选择置乱参数a和b：Arnold置乱的第一步是选择两个置乱参数a和b，这两个参数是用来控制像素排列顺序的。一般情况下，选择两个互质的正整数作为置乱参数，例如a=3，b=5。

2. 将图像转换为矩阵：将要加密的图像转换为一个n×n的矩阵，其中n为矩阵的行数和列数。如果图像大小不是n的整数倍，则可以在图像边缘进行填充或截断操作。

3. 进行置乱操作：对于图像矩阵中的每个像素坐标(x, y)，使用下面的公式进行置乱操作：

   x' = (ax + y) mod n y' = (bx + (a*b+1)*y) mod n

   其中，(x', y')就是置乱后的像素坐标。这个过程就是将图像像素的位置进行混乱和扭曲。

4. 重复置乱操作：对于置乱后的像素坐标(x', y')，再次使用上述公式进行置乱操作，得到新的像素坐标(x'', y'')。重复进行这样的操作，直到达到预设的置乱次数。

5. 将置乱后的像素矩阵转换回图像：将置乱后的像素矩阵重新转换为图像，并保存加密后的图像文件。如果需要对图像进行解密，则需要进行相反的置乱操作。

三、代码实现

1.MATLAB实现置乱

% 定义置乱参数
a = 3;
b = 5;
t = 512;

% 加载要置乱的图像
img = imread('Lena.png');

% 将图像转换为灰度图像
img_gray = rgb2gray(img);

% 将灰度图像转换为矩阵
img_matrix = double(img_gray);

% 获取矩阵的行数和列数
[n, m] = size(img_matrix);

% 对图像进行置乱操作
for k = 1:t % 设置置乱次数为10次
    for i = 1:n
        for j = 1:m
            x = mod(a*i + j, n) + 1;
            y = mod(b*i + (a*b+1)*j, n) + 1;
            img_matrix(x, y) = img_gray(i, j);
        end
    end
end

% 将置乱后的矩阵转换回图像
img_scrambled = uint8(img_matrix);

% 输出Arnold置乱后的图像
imshow(img_scrambled);

% 保存置乱后的图像
imwrite(img_scrambled, 'Lena_scrambled.jpg');

Code_01

% 读取原始图像并转换为灰度图像
img = imread('Lena.png');
img = rgb2gray(img);

% 定义Arnold置乱的参数
n = 512;
a = 3;
b = 5;

% 进行n次Arnold置乱迭代
for k = 1:n
    % 将图像分成大小为n×n的块
    blocks = mat2cell(img, repmat(n, 1, size(img, 1)/n), repmat(n, 1, size(img, 2)/n));
    for i = 1:size(blocks, 1)
        for j = 1:size(blocks, 2)
            % 对于每个块，进行Arnold置乱操作
            block = blocks{i,j};
            [x, y] = meshgrid(1:n, 1:n);
            x1 = mod(a*x + y, n) + 1;
            y1 = mod(b*x + (a*b+1)*y, n) + 1;
            idx = sub2ind([n, n], y1(:), x1(:));
            block = reshape(block(idx), n, n);
            blocks{i,j} = block;
        end
    end
    % 合并所有块并更新图像
    img = cell2mat(blocks);
end

% 输出Arnold置乱后的图像
imshow(img);

Code_02

2.MATLAB实现逆置乱

clear all;
clc;

% 读取图片，根据Arnold变换的条件，图像必须是正方形
img=imread('Lena.bmp');

% 当只有一个输出参数时，返回一个行向量，该行向量的第一个元素时矩阵的行数，第二个元素是矩阵的列数。
mysize=size(img);

if numel(mysize)>2%如果输入是彩色图像
    img=rgb2gray(img); %将彩色到灰度图像的转换
    fprintf("图像为彩色图\n");
else
    fprintf("图像为灰度图\n");
end

imshow(img,[])
title('彩色原图的灰度图');

figure(2)
imhist(img)    %原图的直方图统计

%如果输入的不是正方形图像，则打印如下
[h,w]=size(img);
if h>w
    img = imresize(img, [w w]);
    fprintf("图像长宽不一样，图像可能失真\r");
end
if h<w
    img = imresize(img, [h h]);
    fprintf("图像长宽不一样,图像可能失真");
end
[h,w]=size(img);

% 置乱与逆置乱必须采用共同参数的时候,就相当于密码，才能解密，让图像复原
% 迭代次数
n=10;
a=1;b=1;
N=h;%N代表图像宽高，宽高要一样

%% 置乱操作
imgnnn=zeros(h,w);
for i=1:n
    for y=1:h
        for x=1:w
            xx=mod((x-1)+b*(y-1),N)+1;   %mod取余操作，(a,b)就是a除以b的余数
            yy=mod(a*(x-1)+(a*b+1)*(y-1),N)+1;
            imgnnn(yy,xx)=img(y,x);
        end
    end
    img=imgnnn;
end
imgnnn = uint8(imgnnn);

figure(3)
imshow(img,[])%置乱后的图片
title('置乱后的图片 a=1;b=1，n=10');
imwrite (imgnnn,'置乱后的图片.bmp');  %生成图像保存功能

%% 逆置乱复原
img2=imread('置乱后的图片.bmp');%读取置乱图片
for i=1:n
    for y=1:h
        for x=1:w
            xx=mod((a*b+1)*(x-1)-b*(y-1),N)+1;%matlab索引中不能是0，要从1开始
            yy=mod(-a*(x-1)+(y-1),N)+1  ;
            imgnnn(yy,xx)=img2(y,x);
        end
    end
    img2=imgnnn;
end
imgnnn = uint8(imgnnn);
figure(4)
imshow(imgnnn,[])
title('逆置乱的复原图片');
imwrite(imgnnn,'逆置乱的复原图片.bmp');%生成图像保存功能

Code_03

  在上面的代码中，我们首先定义了置乱参数a和b，然后加载了一张名为lena.jpg的图像，并将其转换为灰度图像。接下来，我们将灰度图像转换为一个n×n的矩阵，然后使用两重循环对每个像素进行置乱操作。在置乱操作中，我们使用了上面描述的公式进行像素坐标的计算和调换。最后，我们将置乱后的矩阵再次转换为图像，并保存到名为lena_scrambled.jpg的文件中。

四、二维Arnold置乱

二维Arnold置乱是一种将二维图像进行混沌置乱的方法，与一维Arnold置乱类似，它也是通过改变像素坐标的排列顺序来实现图像混沌化的。

二维Arnold置乱的具体步骤如下：

1. 选择置乱参数a和b：同样，二维Arnold置乱的第一步是选择两个置乱参数a和b，这两个参数是用来控制像素排列顺序的。一般情况下，选择两个互质的正整数作为置乱参数，例如a=3，b=5。

2. 将图像转换为矩阵：同样地，将要加密的图像转换为一个n×n的矩阵，其中n为矩阵的行数和列数。

3. 进行置乱操作：对于图像矩阵中的每个像素坐标(x, y)，使用下面的公式进行置乱操作：

   x' = (ax + y) mod n y' = (bx + (a*b+1)*y) mod n

   其中，(x', y')就是置乱后的像素坐标。这个过程就是将图像像素的位置进行混乱和扭曲。

4. 重复置乱操作：对于置乱后的像素坐标(x', y')，再次使用上述公式进行置乱操作，得到新的像素坐标(x'', y'')。重复进行这样的操作，直到达到预设的置乱次数。

5. 将置乱后的像素矩阵转换回图像：将置乱后的像素矩阵重新转换为图像，并保存加密后的图像文件。如果需要对图像进行解密，则需要进行相反的置乱操作。

总之，二维Arnold置乱是一种可靠的图像混沌化方法，它可以增强图像的安全性和保密性。