POJ 2976 Dropping tests（分数规划）

http://poj.org/problem?id=2976

题意：

给出ai和bi，ai和bi是一一配对的，现在可以删除k对，使得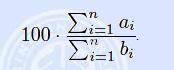的值最大。

思路：

分数规划题，可以参考《挑战程序竞赛》第144页。

枚举答案x，然后去判断是否存在$\frac{\sum a[i]}{\sum b[i]}>=x$，现在把这个式子转换一下，变成$\sum a[i]-x*\sum b[i]>=0$，这样每次贪心选择前面最大的n-k个即可，判断和x的大小关系。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<sstream>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 typedef pair<int,ll> pll;
 const int INF = 0x3f3f3f3f;
 const int maxn=+;
 const double eps=1e-;

 int n, k;
 int a[maxn];
 int b[maxn];
 double tmp[maxn];

 bool check(double x)
 {
     for(int i=;i<n;i++)
         tmp[i]=((double)a[i]-x*b[i]);
     sort(tmp,tmp+n);
     double sum=;
     for(int i=k;i<n;i++)  sum+=tmp[i];
     if(sum>=0.0)  return true;
     else return false;
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     while(~scanf("%d%d",&n,&k))
     {
         if(n== && k==)  break;
         for(int i=;i<n;i++)  scanf("%d",&a[i]);
         for(int i=;i<n;i++)  scanf("%d",&b[i]);

         double ans=;  //刚开始没给ans赋0，wa了很久。。可能会出现k=n的情况...
         double l=,r=;
         while(r-l>=eps)
         {
             double mid=(l+r)/2.0;
             if(check(mid)) {ans=mid;l=mid;}
             else r=mid;
         }
         printf("%d\n",(int)(ans*+0.5));
     }
     return ;
 }