初识 ST 表

推荐博客 ： https://blog.csdn.net/BerryKanry/article/details/70177006

ST表通常用于RMQ问题中，询问某个区间的最值这类问题中

ST表的核心部分就是 st[i][j] ,表示以 i 为起点跳跃 2^j 所经路径的最值。

更新的时候利用dp的思想

代码示例 ：

void init(){
    LOG[0] = -1;
    for(int i = 1; i <= 100000; i++) LOG[i] = LOG[i/2]+1;

    for(int i = 1; i <= LOG[n]; i++){
        for(int j = 1; j+(1<<i)-1 <= n; j++){
            st[j][i] = max(st[j][i-1], st[j+(1<<(i-1))][i-1]);
        }
    }
}

至于查询是可以O（1）实现的

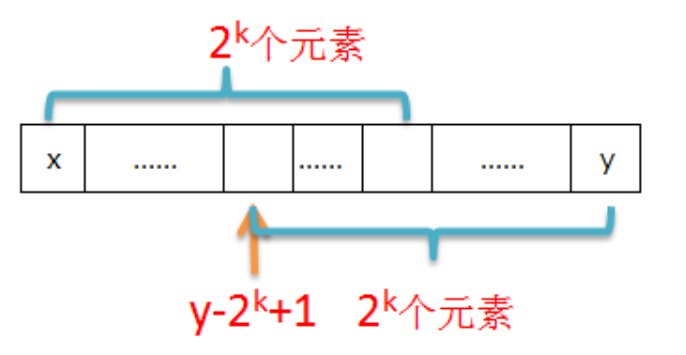
int ans = max(st[a][k], st[b-(1<<k)+1][k]);

还有关于求每个数的对数的LOG数组也是个重点，在上面

int st[maxn][20]; // 最大值为例
int n;
int LOG[maxn];

void init(){
    LOG[0] = -1;
    for(int i = 1; i <= 100000; i++) LOG[i] = LOG[i/2]+1;

    for(int i = 1; i <= LOG[n]; i++){
        for(int j = 1; j+(1<<i)-1 <= n; j++){
            st[j][i] = max(st[j][i-1], st[j+(1<<(i-1))][i-1]);
        }
    }
}

int main() {
    //freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);

    cin >> n;
    for(int i = 1; i <= n; i++){
        scanf("%d", &st[i][0]);
    }
    init();
    //for(int i = 1; i <= n; i++){
        //for(int j = 0; j <= LOG[n]; j++){
            //printf("%d ", st[i][j]);
        //}
        //printf("\n");
    //}
    int m, a, b; // m个查询
    cin >> m;
    for(int i = 1; i <= m; i++){
        scanf("%d%d", &a, &b);

        int k = LOG[b-a+1]
        int ans = max(st[a][k], st[b-(1<<k)+1][k]);
        printf("%d\n", ans);
    }
    return 0;
}