【原】Coursera—Andrew Ng机器学习—编程作业 Programming Exercise 2—

作业说明

　　Exercise 2，Week 3，使用Octave实现逻辑回归模型。数据集 ex2data1.txt ，ex2data2.txt

　　实现 Sigmoid 、代价函数计算Computing Cost 和梯度下降Gradient Descent。

文件清单

ex2.m - Octave/MATLAB script that steps you through the exercise
ex2 reg.m - Octave/MATLAB script for the later parts of the exercise
ex2data1.txt - Training set for the first half of the exercise
ex2data2.txt - Training set for the second half of the exercise
submit.m - Submission script that sends your solutions to our servers
mapFeature.m - Function to generate polynomial features
plotDecisionBoundary.m - Function to plot classifier’s decision boundary
[*] plotData.m - Function to plot 2D classification data
[*] sigmoid.m - Sigmoid Function
[*] costFunction.m - Logistic Regression Cost Function
[*] predict.m - Logistic Regression Prediction Function
[*] costFunctionReg.m - Regularized Logistic Regression Cost

　　* 为必须要完成的

结论

正则化不涉及第一个 θ₀

逻辑回归

　　背景：大学管理员，想要根据两门课的历史成绩记录来每个是否被允许入学。

　　ex2data1.txt ，前两列是两门课的成绩，第三列是y值 0 和 1。

一、绘制数据图

　　 plotData.m：

   positive = find(y == );

   negative = find(y == );

   plot(X(positive,),X(positive,),'k+','MarkerFaceColor','g',

     'MarkerSize',);

   hold on;

   plot(X(negative,),X(negative,),'ko','MarkerFaceColor','y',

     'MarkerSize',);

　　运行效果如下：

二、sigmoid 函数

 function g = sigmoid(z)

 % Instructions: Compute the sigmoid of each value of z (z can be a matrix,

 %               vector or scalar).

   g =  ./ ( + exp(-z));

 end

三、代价函数

　　costFunction.m：

 function [J, grad] = costFunction(theta, X, y)

 　　m = length(y); % number of training examples

 　　part1 = - * y' * log(sigmoid(X * theta));

 　　part2 = ( - y)' * log(1 - sigmoid(X * theta));

 　　J =  / m * (part1 - part2); 

 　　grad =  / m * X' *((sigmoid(X * theta) - y));

 end

四、预测函数

　　输入X和theta，返回预测结果向量。每个值是 0 或 1

 function p = predict(theta, X)

 %PREDICT Predict whether the label is  or  using learned logistic

 %regression parameters theta

 %   p = PREDICT(theta, X) computes the predictions for X using a

 %   threshold at 0.5 (i.e., if sigmoid(theta'*x) >= 0.5, predict 1)

 m = size(X, ); % Number of training examples

 % 最开始没有四舍五入，导致错误

 p = round(sigmoid(X * theta));

 end

五、进行逻辑回归　　

　　ex1.m 中的调用：

　　加载数据：

 data = load('ex2data1.txt');

 X = data(:, [, ]); y = data(:, );

 [m, n] = size(X);

 % Add intercept term to x and X_test

 X = [ones(m, ) X];

 initial_theta = zeros(n + , );

　调用 fminunc 函数

 options = optimset('GradObj', 'on', 'MaxIter', );

 [theta, cost] = ...

     fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);

四、绘制边界线

　　plotDecisionBoundary.m

function plotDecisionBoundary(theta, X, y)

%PLOTDECISIONBOUNDARY Plots the data points X and y into a new figure with

%the decision boundary defined by theta

%   PLOTDECISIONBOUNDARY(theta, X,y) plots the data points with + for the

%   positive examples and o for the negative examples. X is assumed to be

%   a either

%   ) Mx3 matrix, where the first column is an all-ones column for the

%      intercept.

%   ) MxN, N> matrix, where the first column is all-ones

% Plot Data

plotData(X(:,:), y);

hold on

if size(X, ) <=

    % Only need  points to define a line, so choose two endpoints

    plot_x = [min(X(:,))-,  max(X(:,))+];

    % Calculate the decision boundary line

    plot_y = (-./theta()).*(theta().*plot_x + theta());

    % Plot, and adjust axes for better viewing

    plot(plot_x, plot_y)

    % Legend, specific for the exercise

    legend('Admitted', 'Not admitted', 'Decision Boundary')

    axis([, , , ])

else

    % Here is the grid range

    u = linspace(-, 1.5, );

    v = linspace(-, 1.5, );

    z = zeros(length(u), length(v));

    % Evaluate z = theta*x over the grid

    for i = :length(u)

        for j = :length(v)

            z(i,j) = mapFeature(u(i), v(j))*theta;

        end

    end

    z = z'; % important to transpose z before calling contour

    % Plot z =

    % Notice you need to specify the range [, ]

    contour(u, v, z, [, ], 'LineWidth', )

end

hold off

end

正则化逻辑回归

　　背景：预测来自制造工厂的微芯片是否通过质量保证（QA）。在QA期间，每个微芯片都经过两个测试以确保其正常运行。

　　ex2data2.txt ，前两列是测试结果的成绩，第三列是y值 0 和 1。

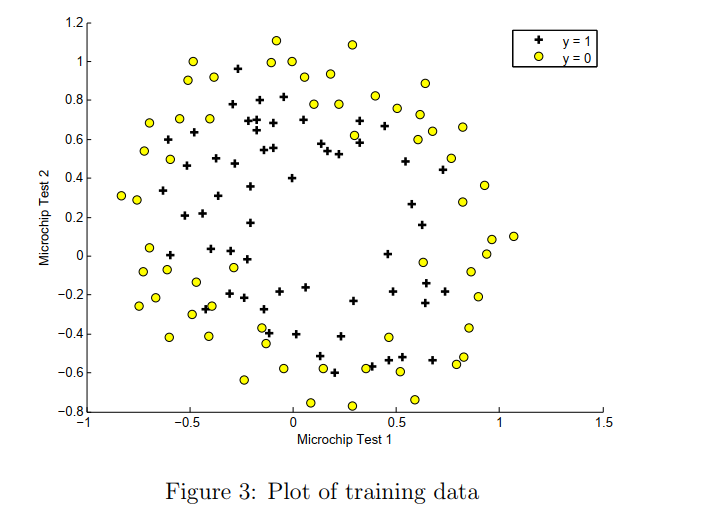
　　只有两个feature，使用直线不能划分。

　　为了让数据拟合的更好，使用mapFeature函数，将x1，x2两个feature扩展到六次方。

　　六次方曲线复杂，容易造成过拟合，所以需要正则化。

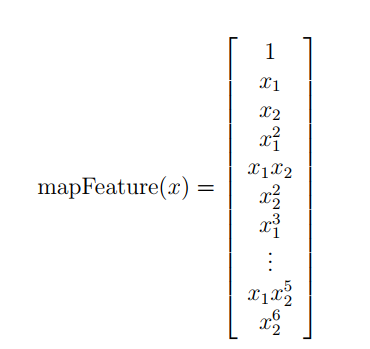
　　mapFeature.m

 function out = mapFeature(X1, X2)

 % MAPFEATURE Feature mapping function to polynomial features

 %

 %   MAPFEATURE(X1, X2) maps the two input features

 %   to quadratic features used in the regularization exercise.

 %

 %   Returns a new feature array with more features, comprising of

 %   X1, X2, X1.^, X2.^, X1*X2, X1*X2.^, etc..

 %

 %   Inputs X1, X2 must be the same size

 %

 degree = ;

 out = ones(size(X1(:,)));

 for i = :degree

     for j = :i

         out(:, end+) = (X1.^(i-j)).*(X2.^j);

     end

 end

 end

二、代价函数

　　注意：θ₀不参与正则化。

　　正则化逻辑回归的代价函数如下，分为三项：

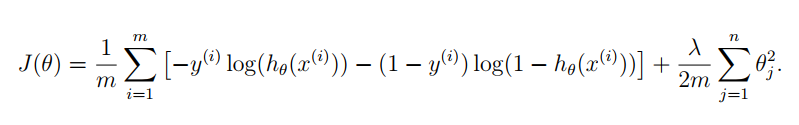
　　梯度下降算法如下：

　　coatFunctionReg.m 如下：

function [J, grad] = costFunctionReg(theta, X, y, lambda)

  m = length(y); % number of training examples


  % theta0 不参与正则化。直接让变量等于theta，将第一个元素置为0，再参与和 λ 的运算

  t = theta;  t() = ; 

  % 第一项

  part1 = -y' * log(sigmoid(X * theta));

  % 第二项

  part2 = ( - y)' * log(1 - sigmoid(X * theta));

  % 正则项

  regTerm = lambda /  / m * t' * t;

  J =  / m * (part1 - part2) + regTerm; 

  % 梯度

  grad =  / m * X' *((sigmoid(X * theta) - y)) + lambda / m * t;

end

　　em2_reg.m 里的调用

% 加载数据
data = load('ex2data2.txt');

X = data(:, [, ]); y = data(:, );


% mapfeature

X = mapFeature(X(:,), X(:,));

% Initialize fitting parameters

initial_theta = zeros(size(X, ), );

lambda = ;


% 调用 fminunc方法

options = optimset('GradObj', 'on', 'MaxIter', );

[theta, J, exit_flag] = ...

    fminunc(@(t)(costFunctionReg(t, X, y, lambda)), initial_theta, options);

三、参数调整

　　（1）使用正则化之前，决策边界曲线如下，可以看到存在过拟合现象：

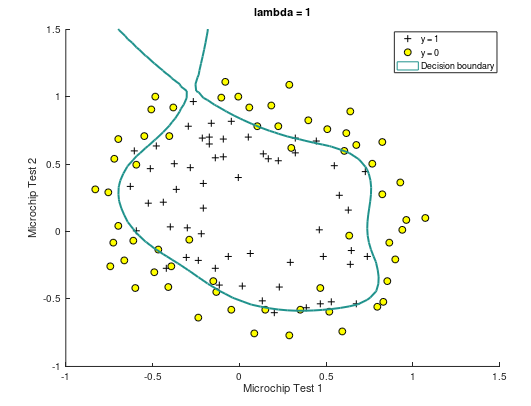
　（2）当 λ = 1，决策边界曲线如下。此时训练集预测准确率为 83.05%

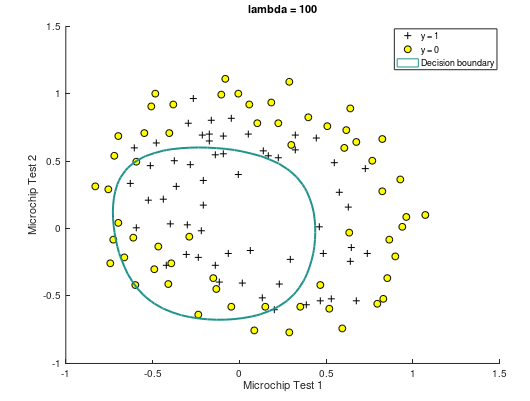
　（3）当 λ = 100，曲线如下。此时训练集预测准确率为 61.01%

完整代码

https://github.com/madoubao/coursera_machine_learning/tree/master/homework/machine-learning-ex2/ex2