Coursera 机器学习 第5章 Neural Networks: Learning 学习笔记

5.1节 Cost Function
神经网络的代价函数。

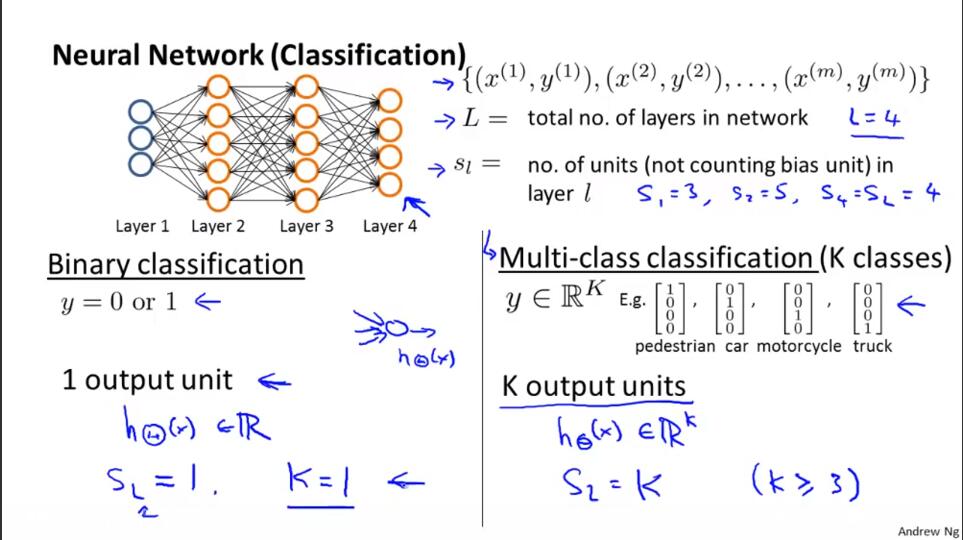
上图回顾神经网络中的一些概念：

L  神经网络的总层数。

s_l  第l层的单元数量（不包括偏差单元）。

2类分类问题：二元分类和多元分类。

上图展现的是神经网络的损失函数，注意这是正则化的形式。

正则化部分，i、j不为0。当然i、j可以为0，此时的损失函数不会有太大的差异，只是当i、j不为0的形式更为常见。

5.2节 Backpropagation Algorithm
最小化损失函数的算法——反向传播算法：找到合适的参数是J(θ)最小。

如上图。最小化损失函数可以使用梯度下降算法或者其他某种高级优化算法。但都需要先计算损失函数和每一项的偏导数。

上图简单回顾前向传播。有4层的网络结构。

Θ⁽ⁱ⁾  第i层到第i+1层的权重

a⁽ⁱ⁾  第i层的激励值

上图简单介绍反向传播算法（只有1个实例）。

1.δ^(l)_j的含义是第l层第j个神经元激励值的误差。

2.S型函数求导的结果：g^'(z)=g(z)*(1-g(z))。写成向量形式就是图中的形式。

3.由后向前求误差。算法实现详细见图。

4.第1层没有误差项。

5.可以证明，忽视正则化部分（λ=0）时，Θ^(l)_ij关于J(Θ)的偏导数正好是a^(l)_j·δ^(l+1)_i。

当有大量实例的时候，后向传播算法的实现如下。其实下面的过程实际主要是求解偏导数的过程：

有训练集{(x^₁,y¹)...(x^m,y^m)}，其中Δ^(l)_ij用来求J(Θ)对Θ^(l)_ij求偏导的结果。

for循环训练集中的每个样例。

每次循环中

1.a⁽¹⁾=x⁽ⁱ⁾，计算前向传播中a^(l)值(l=2，3，...，L)

2.计算偏差项δ^(L)=a^(L)-y⁽ⁱ⁾，然后依次计算δ⁽ⁱ⁾(i=L-1,...,2)

3.累加Δ^(l)_ij=Δ^(l)_ij+a^(j)_l·δ^(l+1)_j

循环退出后，D^(l)_ij表示是J(Θ)对Θ^(l)_ij求偏导的结果，注意区分j=0和j≠0的情况。

5.3节 Backpropagation Intuition
讨论反向传播的复杂步骤，理解这些步骤在做什么。
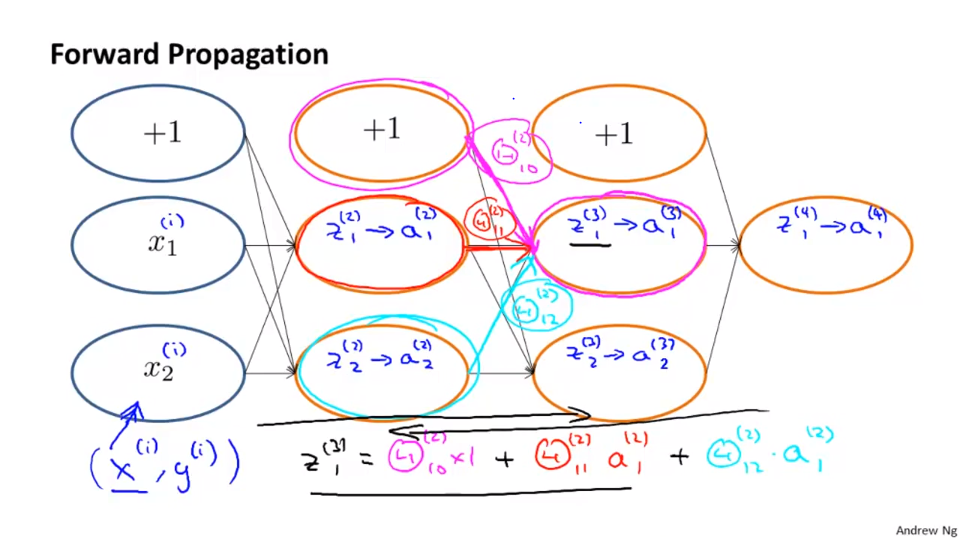
下面是前向传播的原理。比如，z⁽³⁾₁=Θ⁽²⁾₁₀*1+Θ⁽²⁾₁₁*a⁽²⁾₁+Θ⁽²⁾₁₂*a⁽²⁾₂。注意a⁽ⁱ⁾_j=g(z⁽ⁱ⁾_j)。

下图在只有一个输出单元的情况下讨论后向传播的式子。（图上的cost(i)打错）。比如，δ⁽²⁾₂=Θ⁽²⁾₁₂*δ⁽³⁾₁+Θ⁽²⁾₂₂*δ⁽³⁾_2。

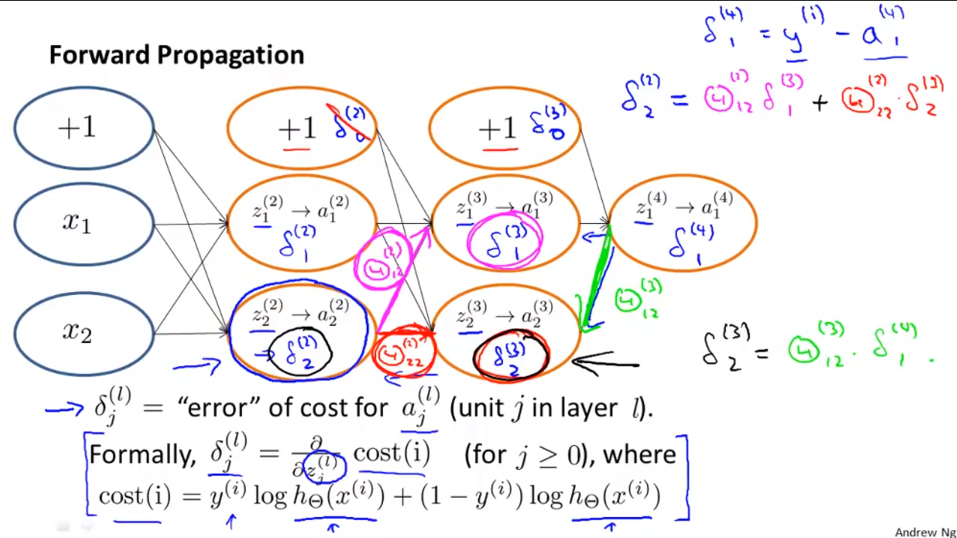
δ是损失函数的关于中间项z的偏微分（为什么？）。δ度量着我们对神经网络的权值做多少改变，对中间的计算量的影响是多少，从而对整个神经网络的输出h(x)的影响是多少，对整个代价值的影响多少。

偏差项对应的δ不是计算微分的必要部分，所以一般忽略。

5.4节 Implementation Note: Unrolling Parameters
上节课讨论了如何使用反向传播算法计算代价函数的导数。这节课介绍参数的矩阵形式和向量形式之间的转换的实现过程，怎样把参数从矩阵展开成向量，以便在高级的最优化步骤中使用。

上图中，矩阵D是返回的梯度值gradient（损失函数关于特定参数Θ的偏导数）。

逻辑回归中，先写出损失函数的形式，然后调用高级的优化算法（这里是fminunc）。将损失函数、初始参数向量Θ(theta)、迭代要求作为参数输入，然后返回处理后的最优参数向量Θ。但是在神经网络中Θ是矩阵形式而不是向量形式，因此需要转换形式。

举个具体的例子：

上图是一个4层的神经网络系统（图中画错）。

将矩阵形式的Theta参数展开成向量形式thetaVec：thetaVec=[Theta1(:);Theta2(:);Theta3(:)]

将向量形式的thetaVec的前1-110个元素恢复成矩阵形式10*11的Theta1：Theta1=reshape(thetaVec(1:110),10,11)

基本算法综述：

1.fminunc函数中，将初始权重矩阵参数Θ⁽¹⁾、Θ⁽²⁾、Θ⁽²⁾展开成向量形式的initialTheta。将initialTheta作为形参传入fminunc函数。

2.代价函数中，向量形式的thetaVec转换为矩阵形式的Θ⁽¹⁾、Θ⁽²⁾、Θ⁽²⁾，利用前向/后向传播计算D⁽¹⁾、D⁽²⁾、D⁽³⁾和J(Θ)。展开D⁽¹⁾、D⁽²⁾、D⁽³⁾形成gradientVec返回。

矩阵形式的好处是在进行前向传播和反向传播的时候，会觉得更加方便，充分利用了向量化的实现过程。向量形式的好处是有像thetaVec或者DVec这样的矩阵，当你使用一下高级的优化算法的时候，这些算法通常要求所有参数要展开成一个长向量的形式。

5.5节 Gradient Checking
反向传播作为一个有很多细节的算法，在实现的时候会有点复杂。而且在实现反向传播的时候会遇到很多细小的错误，所以如果你把它和梯度下降法或者其他优化算法一起运行时，可能看起来它运行正常，并且你的代价函数J(Θ)最后在每次梯度下降法迭代时都会减小，但是可能你最后得到的神经网络误差比没有错误的要高，而且你很可能就是不知道是这些小错误导致的。

这里有个可以及时验证是否出错的方法：梯度检验。这个方法适用于比较复杂的模型，用于验证算法实现是否出错。

在这里，梯度检验：用来区别反向传播实现是否正确的方法。

先看导数的近似值的求解：

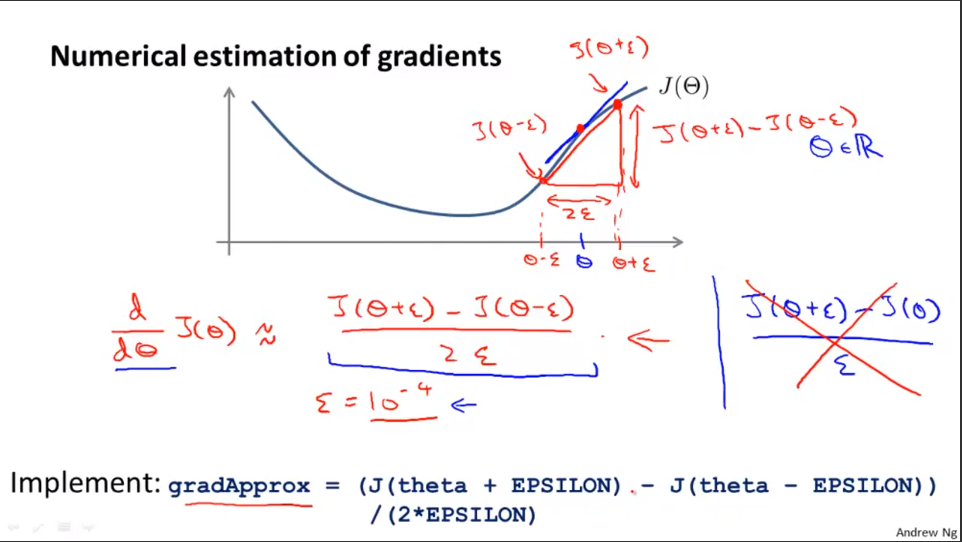
单侧差分和双侧差分，这里用双侧差分。

一个课后练习：

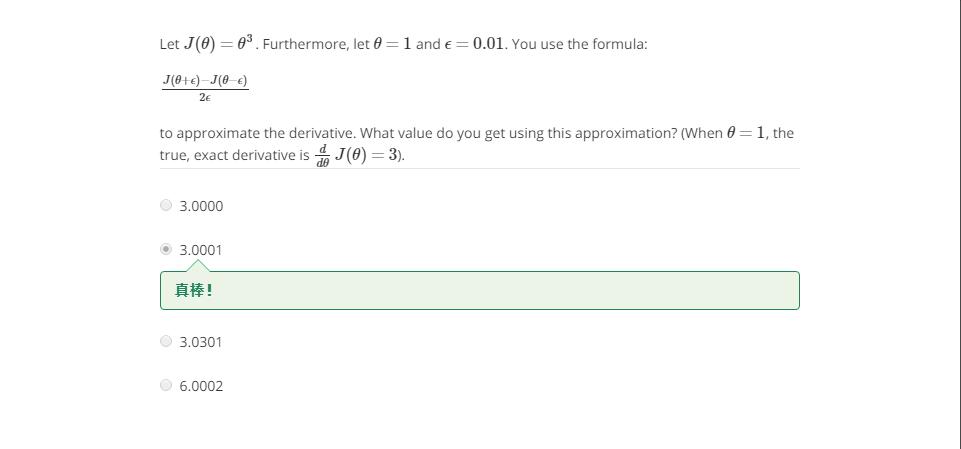
梯度检验的思想是计算偏导数的数值近似值向量gradApprox，然后和用便捷方法求出的DVec进行比较，如果结果差不多，之前的求解就是正确的。

数学形式：

总结：

1.使用反向传播计算DVec。

2.利用梯度检验计算gradApprox。

3.比较DVec和gradApprox数值大小。

4.关闭梯度检验。将反向传播代码用于学习。

注意关掉梯度检验。因为梯度检验要比反向传播更慢。

5.6节 Random Initialization
这里要介绍随机初始化。
在逻辑回归中，设定theta初始值为0是可行的的，但是在神经网络中是不可行的。如果初始值相同，到最后所有的theta都相同，没有训练的意义。实际上，对于第l层，Θ^(l)为矩阵，该矩阵所有权重初始值相同就会出现问题。这个问题也称为对称权重。

比如下图的例子：

如果Θ^(l)_ij都初始化为同一个值，在图中可以看到，前向传播中，a⁽²⁾₂=a⁽²⁾₁；后向传播中，δ⁽²⁾₁=δ⁽²⁾_2，从而∂J(Θ)/∂(Θ⁽¹⁾₁₁)=∂J(Θ)/∂(Θ⁽¹⁾₂₁)。那么使用梯度下降时，Θ⁽¹⁾₁₁=Θ⁽¹⁾₁₁-α*∂J(Θ)/∂(Θ⁽¹⁾₁₁)，Θ⁽¹⁾₂₁=Θ⁽¹⁾₂₁-α*∂J(Θ)/∂(Θ⁽¹⁾₂₁)。于是，最后Θ⁽¹⁾₁₁=Θ⁽¹⁾₂₁。同理，Θ⁽¹⁾₁₀=Θ⁽¹⁾_{20，Θ⁽¹⁾12=Θ⁽¹⁾22}。也就是说，经过梯度下降算法后，仍然有a⁽²⁾₂=a⁽²⁾₁，就好像第一层隐藏层所有单元都在计算相同的特征，所有的隐藏单元都在计算相同的输入函数，最后输出层每个单元输出值相同。所以，初始化参数Θ时，对第l层的权重矩阵Θ^(l)，不能将Θ^(l)_ij元素都初始为同一值。

这里做题：

答案：BD

rand(a,b)  申请一个a*b的矩阵，矩阵元素大小在(0,1)。

总体来说，对权重进行随机初始化，然后反向传播，再执行梯度检查（使用梯度下降或者高级的优化算法）

5.7节 Putting It Together
对神经网络算法的所有的内容做一个总体的回顾。

神经网络的第一步是构建大体的框架：

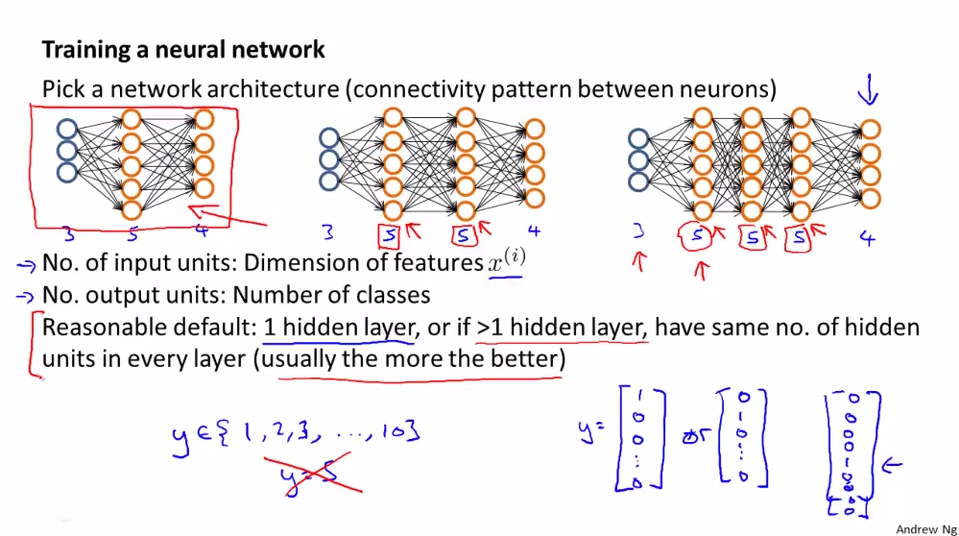
图中最左边是最基本的神经网络结构：输入层、隐藏层、输出层。

注意，如果有多个隐藏层，默认每个隐藏层神经单元数量相同。一般输入层神经单元个数就是实例的维度，输出层神经单元个数就是类别的个数。一般而言，隐藏层神经单元个数越多越好，但是计算量也会相应的增加。隐藏单元的数量要和其他参数相匹配。

下面实现神经网络的训练过程，共6步：

1.随机初始化权重，初始化的权重值一般较小。

2.为每x⁽ⁱ⁾执行前向传播，算出h_Θ(x⁽ⁱ⁾)。

3.执行J(Θ)的计算代码。

4.执行反向传播，计算偏导数∂J(Θ)/∂(Θ⁽¹⁾_jk)。对m个测试实例，使用for循环，计算激励值a和Δ和δ。

5.对偏导数∂J(Θ)/∂(Θ⁽¹⁾_jk)进行梯度检验。偏导数代码没有问题后，关闭梯度检验部分代码。

6.使用梯度下降或者其他高级算法执行反向传播，求出最小化J(Θ)时的各Θ值。

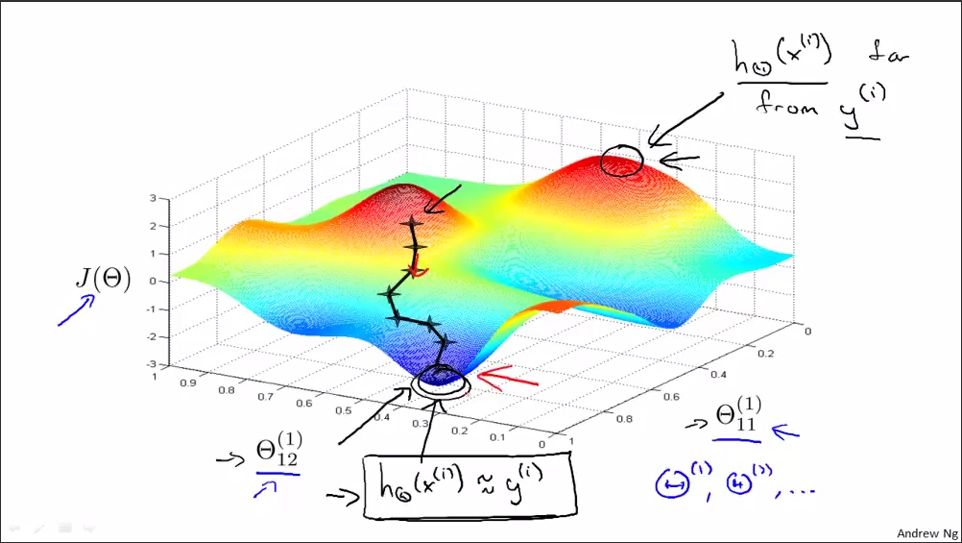
结合下图对神经网络中的梯度下降算法进行说明：从随机的初始点开始，一步一步地下降，直到取得局部最优值。像梯度下降这样的算法至少可以保证收敛到局部最优值。反向传播算法的目的是计算出梯度下降的方向，使代价函数不断减少至局部最优值。

5.8节 Autonomous Driving
介绍一个神经网络学习的重要例子：利用神经网络实现自动驾驶。

练习：

答案：BD

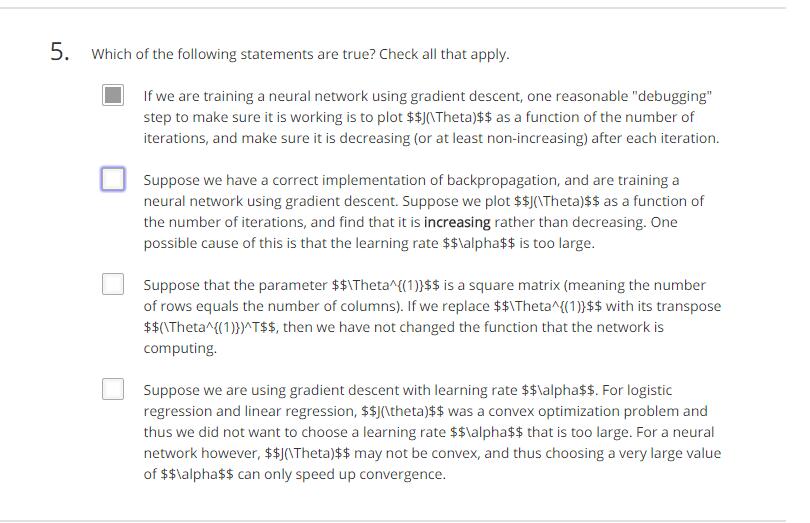
答案：AB

答案：BC

课程对应的作业不要忘记，对梳理知识很有帮助。

注意2点：

1.正则化代价函数中的正则化部分不能将偏差项引出的权重theta计算在内。
正则化公式：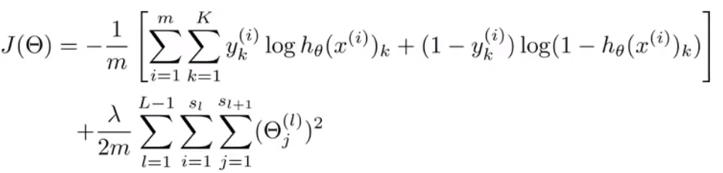

2.反向传播中，计算权重对应的偏导数时，所有由偏差项（偏差神经单元）引出的权重对应的δ都不必计算。