HDU 6321 (状压dp)

题目大意::

为给你n个点（n<=10,nn<=10,n）
初始时没有边相连
然后有m个操作（m<=30000m<=30000）
每次可以添加一条边或删除一条边
允许有重边
要求每次操作过后输出选这个图中不相交的k条边有多少种不同的方案
（k=1,2,3……n/2）

题目分析：

n最大只有10 ， 所以很容易就可以想到状压DP , 但是我在打的时候并没有想出继承状态 ， 后来看了题解才略有一丝感悟；

首先一个特别容易看出的状态是每加/减一条边后的状态是由前一个状态转移过来的 ；

而因为本状态是由上一个状态转移而来，因而我们可以考虑设立一个二维的dp数组，dp[now][s]。代表了在当前的状态now中集合数为s的匹配数。因此我们可以找到第一条状态转移的方程 dp[now][i]= dp[pre][i]. 我只能想到了这个Orz , 下面的状态转移 ， 可以说是挺显然的 ，而我并没有看出。。

在每进行一次加边的过程中，我们可以发现，假设加的一条边在前一个状态没有出现过，那么加上这条边之后的状态是由前一个状态的匹配数的基础上转移而来的，因此有状态转移方程

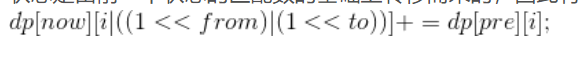
同理，在每一次减边的过程中，如果减的两条边在前一个状态没有出现过的话，则在减去这条边后的状态是由前一个状态转移而来的，故有转移方程

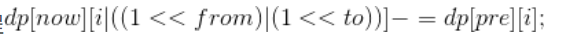
将所有方案的匹配数求完之后，只需统计一下答案即可。

题解参考与chen大牛

#include <bits/stdc++.h>
#define maxn 2005
using namespace std;
const int mod=1e9+;
int dp[][maxn];///用滚动数组压缩
int cnt[maxn];
int ans[maxn];
char str[];
int bit(int x){//获取某个数二进制位上有多少个1
    int cnt=;
    while(x){
        if(x&) cnt++;
        x>>=;
    }
    return cnt;
}
void init(){//初始化处理二进制位上1的个数
    for(int i=;i<;i++){
        cnt[i]=bit(i);
    }
}
int main()
{
    int t;
    scanf("%d",&t);
    init();

    while(t--){
        int n,m;int now=,pre=;
        scanf("%d%d",&n,&m);
        int all=<<n;
        memset(dp,,sizeof(dp));
        dp[][]=;
        while(m--){
            scanf("%s",str);
            int from,to;
            scanf("%d%d",&from,&to);
            from--,to--;
            int tmp=(<<from)|(<<to);//代表第from位和第to位有一条边
            for(int i=;i<all;i++){//先进行状态转移
                dp[now][i]=dp[pre][i];
            }
            if(str[]=='+'){
                for(int i=;i<all;i++){
                    if(!(tmp&i)){//如果没加上
                        dp[now][i|tmp]=(dp[now][i|tmp]+dp[pre][i])%mod;
                    }
                }
            }
            else{
                for(int i=;i<all;i++){
                    if(!(tmp&i)){//如果没减去
                        dp[now][i|tmp]=(dp[now][i|tmp]-dp[pre][i]+mod)%mod;
                    }
                }
            }
            memset(ans,,sizeof(ans));
            for(int i=;i<all;i++){//统计答案
                ans[cnt[i]]=(ans[cnt[i]]+dp[now][i])%mod;
            }
            for(int i=;i<=n;i+=){///一个匹配数需要2个点
                if(i!=) cout<<" ";
                cout<<ans[i];
            }
            puts("");
          //  printf("%d %d\n",pre,now);
            pre^=,now^=;
         //   printf("%d %d\n",pre,now);
        }
    }
}