cf 786 B 线段树优化建图

cf 786 B

链接

CF

思路

n个点，3种建边方式，规模\(O(n^2)\)

线段树优化建图

注意

读入的数据好坑啊，说好的v,u变成了u,v。

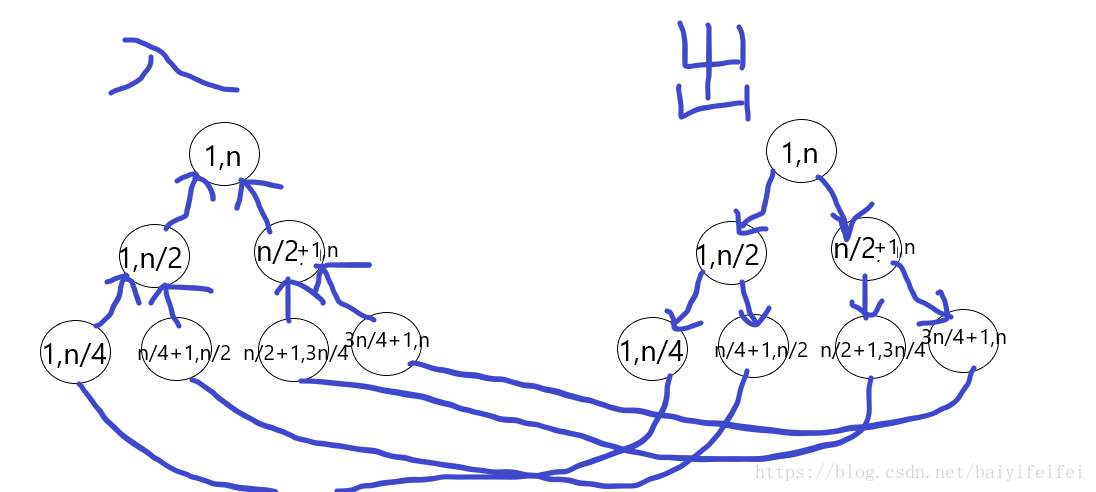
两棵树，一棵出，一棵入。线段树的作用只不过是按照那个形状建边而已，并没啥用。

初始父亲儿子连边,两棵树的叶子结点一一连边，边权为0。(实际中可以直接共用叶子结点)

大佬的图很不错，引用一下



然后在把其他关系引用到上面就行了

代码

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=5e5+7;
int read() {
    int x=0,f=1;char s=getchar();
    for(;s>'9'||s<'0';s=getchar()) if(s=='-') f=-1;
    for(;s>='0'&&s<='9';s=getchar()) x=x*10+s-'0';
    return x*f;
}
int n,q,S;
struct node {
    int v,nxt;
    ll q;
}G[N<<4];
int head[N<<3],tot,cnt;
void add(int u,int v,int q,int opt) {
    if(opt) swap(u,v);
    G[++tot].v=v;
    G[tot].q=q;
    G[tot].nxt=head[u];
    head[u]=tot;
}
struct seg {
    #define ls rt<<1
    #define rs rt<<1|1
    int id[N<<3];
    void build(int l,int r,int rt,int opt) {
        if(l==r) return id[rt]=l,void();
        id[rt]=++cnt;
        int mid=(l+r)>>1;
        build(l,mid,ls,opt);
        build(mid+1,r,rs,opt);
        add(id[rt],id[ls],0,opt);
        add(id[rt],id[rs],0,opt);
    }
    void modify(int L,int R,int u,int q,int l,int r,int rt,int opt) {
        if(L<=l&&r<=R) return add(u,id[rt],q,opt);
        int mid=(l+r)>>1;
        if(L<=mid) modify(L,R,u,q,l,mid,ls,opt);
        if(R>mid) modify(L,R,u,q,mid+1,r,rs,opt);
    }
}a,b;
struct edge {
    int id;
    ll val;
    edge(int a=0,ll b=0) {id=a,val=b;}
    bool operator < (const edge &b) const {
        return val>b.val;
    }
};
priority_queue<edge> Q;
ll dis[N];
void dij() {
    memset(dis,0x3f,sizeof(dis));
    dis[S]=0;
    Q.push(edge(S,0));
    while(!Q.empty()) {
        edge u=Q.top();
        Q.pop();
        if(dis[u.id]!=u.val) continue;
        for(int i=head[u.id];i;i=G[i].nxt) {
            int v=G[i].v;
            if(dis[v]>dis[u.id]+G[i].q) {
                dis[v]=dis[u.id]+G[i].q;
                Q.push(edge(v,dis[v]));
            }
        }
    }
}
int main() {
    n=cnt=read(),q=read(),S=read();
    a.build(1,n,1,0);
    b.build(1,n,1,1);
    for(int i=1;i<=q;++i) {
        int opt=read();
        if(opt==1) {
            int u=read(),v=read(),w=read();
            add(u,v,w,0);
        } else if(opt==2) {
            int u=read(),l=read(),r=read(),w=read();
            a.modify(l,r,u,w,1,n,1,0);
        } else if(opt==3) {
            int u=read(),l=read(),r=read(),w=read();
            b.modify(l,r,u,w,1,n,1,1);
        }
    }
    dij();
    for(int i=1;i<=n;++i) {
        if(dis[i]==0x3f3f3f3f3f3f3f3fLL) dis[i]=-1;
        printf("%I64d ",dis[i]);
    }
    return 0;
}