机器学习-无监督机器学习-kmeans-17

目录

• 1. 什么是聚类
• 2. 代码实现

1. 什么是聚类

无监督机器学习的一种 输入数据只有X 没有y

将已有的数据 根据相似度 将划分到不同的簇 （花团锦簇）

步骤：

1. 随机选择k个簇的中心点
2. 样本根据距离中心点的距离分配到不同的簇
3. 重新计算簇的中心点
4. 重复 2-3直到所有样本 分配的簇不再发生改变

距离的计算：

1. Euclidean Distance 欧式距离
   
   

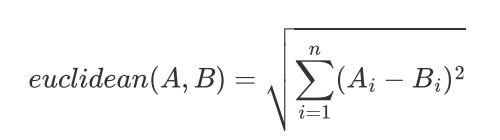
2. 余弦距离
   
   两个向量的夹角余弦值 -1 +1：
   
   
   
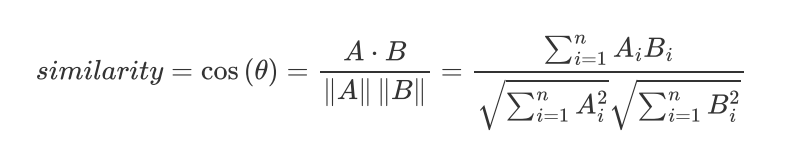
   1-cos(theta) 称为余弦距离

欧氏距离体现数值上的绝对差异，而余弦距离体现方向上的相对差异

cosine相似度更适用于文本

举例：

后面两篇文章来自同一篇，余弦距离测度更准确，因为来自相同的分布，

归一化之后两种测量方式存在单调关系 选择谁都一样：

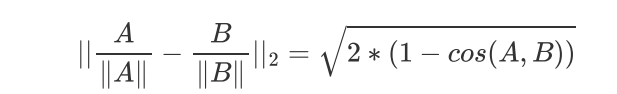
kmeans算法的目标函数：

每个簇里面 元素距离中心点的距离最小

算法不保证找到最好的解，目标函数是非凸函数，通常的做法就是运行KMeans很多次，每次随机初始化不同的初始中心点，然后从多次运行结果中选择最好的局部最优解

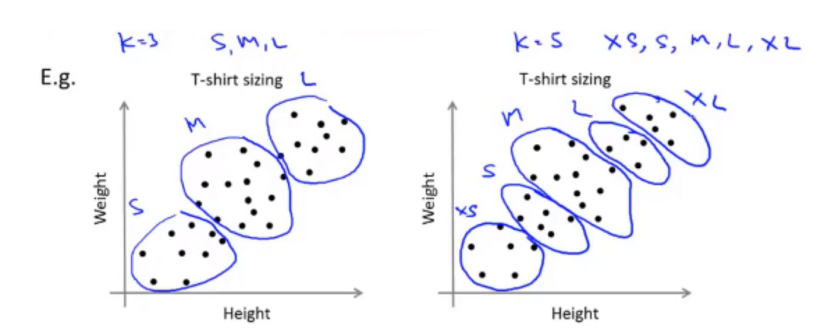
聚类簇的 数目k的选择：

改变聚类数K，然后进行聚类，计算损失函数，拐点处即为推荐的聚类数

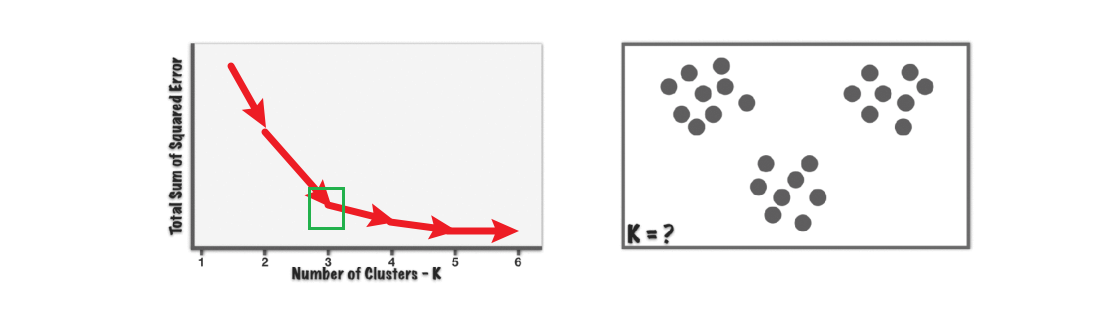
聚类本身是为了有监督任务服务的

例如聚类产生features【譬如KMeans用于某个或某些个数据特征的离散化】然后将KMeans离散化后的特征用于下游任务），则可以直接根据下游任务的metrics进行评估更好

例如：衣服尺寸的分类

2. 代码实现

#!/usr/bin/env python
# coding: utf-8

# In[6]:

import random
import numpy as np
from sklearn.feature_extraction.text import TfidfVectorizer

# In[3]:

def disCos(vecA, vecB):
    return np.dot(vecA, vecB)/(np.sqrt(np.sum(np.square(vecA)))*np.sqrt(np.sum(np.square(vecB))))

# In[4]:

def disEclud(vecA, vecB):
    return np.sqrt(np.sum(np.power(vecA-vecB, 2)))

# In[22]:

def ranCent(dataSet, k):
    m, n = dataSet.shape
    index_list = list(range(m))
    np.random.shuffle(index_list)
    centroids = dataSet[index_list][:k]
    return centroids

# In[44]:

def kMeans(dataSet, k, disMeans=disEclud):
    m, n = dataSet.shape

    clusterAssment = np.zeros((m, 2))  # 用于存放 属于哪一类 以及距离该类中心点的距离
    centroids = ranCent(dataSet, k)

    clusterChanged = True

    while clusterChanged:
        clusterChanged = False

        # 1. 将样本点 根据距离最近 划分到所属类别

        for i in range(m):
            minDist = float("inf")
            minIndex = -1

            for j in range(k):
                distJI = disMeans(centroids[j, :], dataSet[i, :])
                if distJI < minDist:
                    minDist = distJI
                    minIndex = j
            if clusterAssment[i, 0] != minDist:
                clusterChanged = True # 距离有变化
            clusterAssment[i, :] = minIndex, minDist**2  # 将每个样本的所属类别 以及距离 存入
        print(centroids)
        # 2. 更新每个类的中心点
        for cent in range(k):
            ptsInCluster = dataSet[np.nonzero(clusterAssment[: 0] == cent)]  # 属于该类别的所有x取出
            centroids[cent, :] = np.mean(ptsInCluster, axis=0)

    return centroids, clusterAssment          

# In[47]:

import jieba
doc1 = '我爱北京北京天安门'
doc2 = '我爱北京颐和园'

doc3 = "世界杯梅西夺冠"

doc4 = "世界杯精彩"

docs = [doc1, doc2, doc3, doc4]
docs = [" ".join(list(jieba.cut(sentence))) for sentence in docs]

X = TfidfVectorizer().fit_transform(docs)
result = kMeans(X.A, k=2, disMeans=disCos)
result

# In[48]:

a = np.array([[1, 2], [2, 4], [3, 6]])
a

# In[49]:

a[:, 0] # 取出第一个维度

# In[50]:

a[:, 1]

# In[53]:

np.mean(a, axis=0)  # 沿着 竖直方向求平均