Educational Codeforces Round 105 (Rated for Div. 2) A-C题解

写在前边

链接：Educational Codeforces Round 105 (Rated for Div. 2)

A. ABC String

链接：A题链接

题目大意:

给定一个有\(A、B、C\)大写字母组成的字符串，然后让我们用\('('\)与\(')'\)来替换三个字母，同类的字母只能用一种类型的括号，问组成的括号序列是否是合法的括号序列。

思路：

发现一个性质，位于左边第一个的字母只能用'('，位于右边第一个的字母只能用')'，因此左右两边不能是同一个字母，所以这就有两个字母所用的括号确定了，剩下那个只需要构造成数量较少的那个类型的括号就好了，然后字符串构造出来之后就用栈检查一下。

代码:

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <vector>
#include <map>
#include <cstring>
#include <stack>

//#pragma GCC optimize(2)
//#pragma GCC optimize(3,"Ofast","inline")

using namespace std;

#define Inf 0x3f3f3f3f
#define PII pair<int, int>
#define P2LL pair<long long, long long>
#define endl '\n'

typedef long long LL;
typedef unsigned long long ULL;
typedef vector<long long> VLL;
typedef vector<int> VI;

const int Mod = 10000007;

void solve() {
    string s;
    cin >> s;
    int n = s.length();
    if (s[0] == s[n - 1]) {
        puts("NO");
        return;
    }
    map<char, int> mp;
    for (int i = 0; i < n; i++) mp[s[i]]++;

    string ss = "";
    for (int i = 0; i < n; i++) {
        if (s[i] == s[0]) ss += '(';
        else if (s[i] == s[n - 1]) ss += ')';
        else ss += (mp[s[0]] > mp[s[n - 1]] ? ')' : '(');
    }

    stack<int> st;
    for (int i = 0; i < ss.size(); i++) {
        if (ss[i] == '(') st.push(ss[i]);
        else if (ss[i] == ')') {
            if (st.empty()) {
                puts("NO");
                return;
            }
            if (st.size()) st.pop();
        }
    }

    if (st.empty()) puts("YES");
    else puts("NO");
}

int main()
{
    //ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
    int t;
    scanf("%d", &t);
    while (t--) {
        solve();
    }

    return 0;
}

B. Berland Crossword

链接：B题链接

题目大意:

给定\(u,r,d,l\)四个量，表示在一个\(n*n\)的网格中上边有\(u\)个涂黑，右边有\(r\)个涂黑，下边有\(d4个涂黑，左边有\)l$个涂黑，问是否能满足要求。

思路：

由于只由在拐角处的方格能影响相邻的一行和一列，因此我们只需要二进制枚举四个拐角然后判断一行或一列中中间的网格（由\(n-2\)个）是否能装下需要的网格即可。

代码:

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <vector>
#include <map>
#include <cstring>

//#pragma GCC optimize(2)
//#pragma GCC optimize(3,"Ofast","inline")

using namespace std;

#define Inf 0x3f3f3f3f
#define PII pair<int, int>
#define P2LL pair<long long, long long>
#define endl '\n'

typedef long long LL;
typedef unsigned long long ULL;
typedef vector<long long> VLL;
typedef vector<int> VI;

const int Mod = 10000007;

LL gcd(LL a, LL b) {
    return b ? gcd(b, a % b) : a;
}

void change(int x, int &u, int &r, int &d, int &l) {
    switch (x) {
        case 0:
            u--, l--;
            break;
        case 1:
            u--, r--;
            break;
        case 2:
            r--, d--;
            break;
        case 3:
            l--, d--;
            break;
    }
}

void solve() {
    int n, u, r, d, l;
    cin >> n >> u >> r >> d >> l;

    for (int mask = 0; mask < (1 << 4); mask++) {
        int uu = u, rr = r, dd = d, ll = l, q;
        for (int j = 0; j < 4; j++) {
            if (mask >> j & 1) change(j, uu, rr, dd, ll); //搞四个角
        }
        if (uu < 0 || rr < 0 || dd < 0 || ll < 0) { //如果光角上放的就大于需要了
            continue;
        }
        int re = n - 2;
        if (re >= uu && re >= rr && re >= dd && re >= ll) {
            puts("YES");
            return;
        }
    }
    puts("NO");
}

int main()
{
    //ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
    int t;
    scanf("%d", &t);
    while (t--) {
        solve();
    }
    return 0;
}

C. 1D Sokoban

链接：B题链接

题目大意:

推箱子游戏，最初一个人站在\(0\)点，有\(n\)个箱子分布在左右两侧，只能往左边或往右边推箱子，并且不能跨过一个箱子去推当前箱子后边的箱子，如果正在推的当前箱子后边还有一个箱子，那么推的时候后边的箱子会跟着动，然后还有\(m\)个特殊位置，求经过一定的推箱子操作后使得有多少个箱子在特殊位置上，求这个最大值。

思路：

一开始没有看到不能跨过箱子这个条件，然后贪心加二分搞了一个多小时\(WA\)了，然后又根据正确思路，码出来了，花了昨晚一晚上和今天两个小时。。好怀疑人生。

思路就是：首先明白，对于负数的位置和正数的位置我们需要分开操作，并且操作相同，然后我们可以看答案是怎么被贡献得到的，可以枚举每一个特殊位置，假设当前页数位置为\(k\)：

对于\(>k\)的数轴位置上，我们还没有推到，所以说这一部分的就是原本就在特殊位置上的箱子

那么对于\(\leq k\)的数轴位置上，这一部分箱子是我们一直推到\(k\)的，也就是说在位置\(k\)以及之前有一串箱子，画个图就是这样：



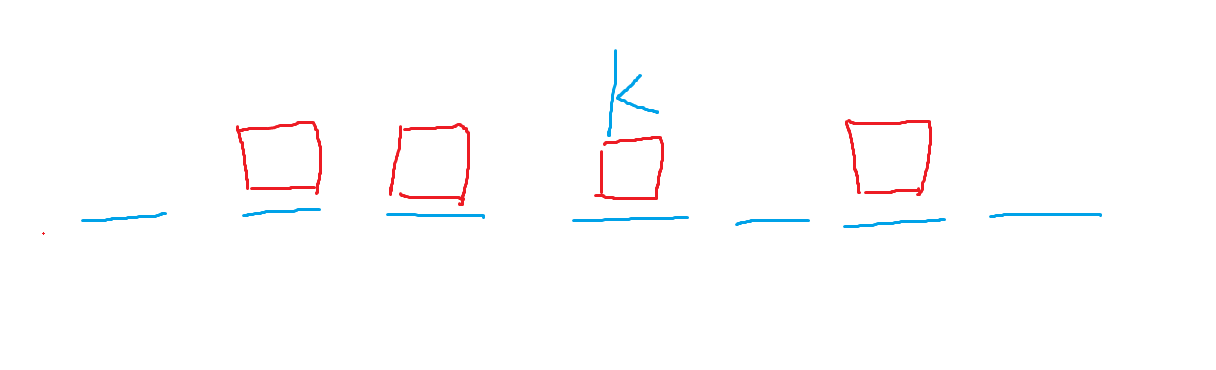
那么对于\(k\)这个状态，答案就是后一部分已经在特殊位置上的箱子数和在它所处位置以及之前的所有箱子所覆盖的特殊点的数量之和。

那么对于后一部分，就可以直接用一个后缀和来维护。

对于前一部分，我们需要算出那个连续的子段覆盖了多少特殊点，那么这里怎么求呢，用两个二分即可。

第一个二分是求出在当前位置\(k\)以及之前有多少个箱子，即子段的长度，记为:\(num\)。

第二个二分，求出第一个大于等于最左边箱子的特殊位置的点。

更新答案。

代码:

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <vector>
#include <map>
#include <cstring>

//#pragma GCC optimize(2)
//#pragma GCC optimize(3,"Ofast","inline")

using namespace std;

#define Inf 0x3f3f3f3f
#define PII pair<int, int>
#define P2LL pair<long long, long long>
#define endl '\n'
#define pub push_back
#define pob pop_back

typedef long long LL;
typedef unsigned long long ULL;
typedef vector<long long> VLL;
typedef vector<int> VI;

const int Mod = 10000007;

int cal(VI& box, VI& pos) {
    int n = box.size(), m = pos.size();
    VI suff(m + 2);
    map<int, int> tag;
    for (int i = 1; i < n; i++) tag[box[i]] = 1;

    for (int i = m - 1; i >= 1; i--) {
        suff[i] = suff[i + 1] + tag[pos[i]]; //处理寻找有多少个箱子在特殊位置上
    }
    int res = suff[1];
    for (int i = 1; i < m; i++) {
        int num = upper_bound(box.begin() + 1, box.end(), pos[i]) - box.begin() - 1;//计算出有多少个箱子在当前位置左边
        //upper_bound第一个大于pos[i]的位置，那么减一就是第一个小于等于pos[i]的位置的箱子。
        int left = lower_bound(pos.begin() + 1, pos.end(), pos[i] - num + 1) - pos.begin();
        res = max(res, i - left + 1 + suff[i + 1]);
    }

    return res;
}

void solve() {
    int n, m;
    scanf("%d%d", &n, &m);

    VI positiveA, positiveB, negativeA, negativeB;
    positiveA.pub(-1), negativeA.pub(-1);
    positiveB.pub(-1), negativeB.pub(-1);
    for (int i = 0; i < n; i++) {
        int a;
        scanf("%d", &a);
        if (a > 0) positiveA.pub(a);
        if (a < 0) negativeA.pub(-a);
    }
    for (int i = 0; i < m; i++) {
        int b;
        scanf("%d", &b);
        if (b > 0) positiveB.pub(b);
        if (b < 0) negativeB.pub(-b);
    }

    reverse(negativeA.begin() + 1, negativeA.end());
    reverse(negativeB.begin() + 1, negativeB.end());

    printf("%d\n", cal(positiveA, positiveB) + cal(negativeA, negativeB));
}

int main()
{
    //ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
    int t;
    scanf("%d", &t);
    while (t--) {
        solve();
    }

    return 0;
}