文心一言 VS 讯飞星火 VS chatgpt （158）-- 算法导论12.3 5题

五、用go语言，假设为每个结点换一种设计，属性 x.p 指向 x 的双亲，属性 x.succ 指向 x 的后继。试给出使用这种表示法的二叉搜索树 T 上 SEARCH、INSERT 和DELETE 操作的伪代码。这些伪代码应在 O(h) 时间内执行完，其中 h 为树 T 的高度。(提示：应该设计一个返回某个结点的双亲的子过程。)

文心一言：

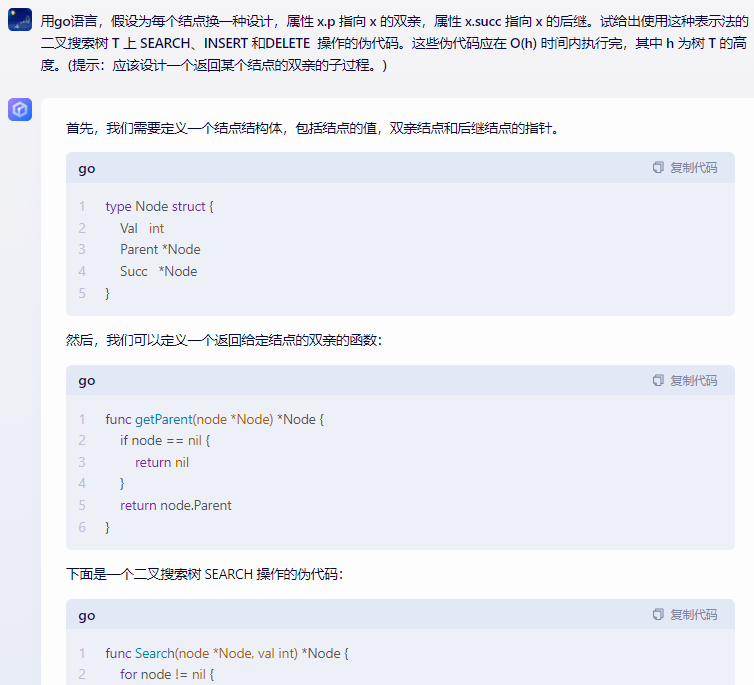
首先，我们需要定义一个结点结构体，包括结点的值，双亲结点和后继结点的指针。

type Node struct {
    Val   int
    Parent *Node
    Succ   *Node
}

然后，我们可以定义一个返回给定结点的双亲的函数：

func getParent(node *Node) *Node {
    if node == nil {
        return nil
    }
    return node.Parent
}

下面是一个二叉搜索树 SEARCH 操作的伪代码：

func Search(node *Node, val int) *Node {
    for node != nil {
        if node.Val == val {
            return node
        } else if node.Val < val {
            node = node.Succ
        } else {
            node = getParent(node)
        }
    }
    return nil
}

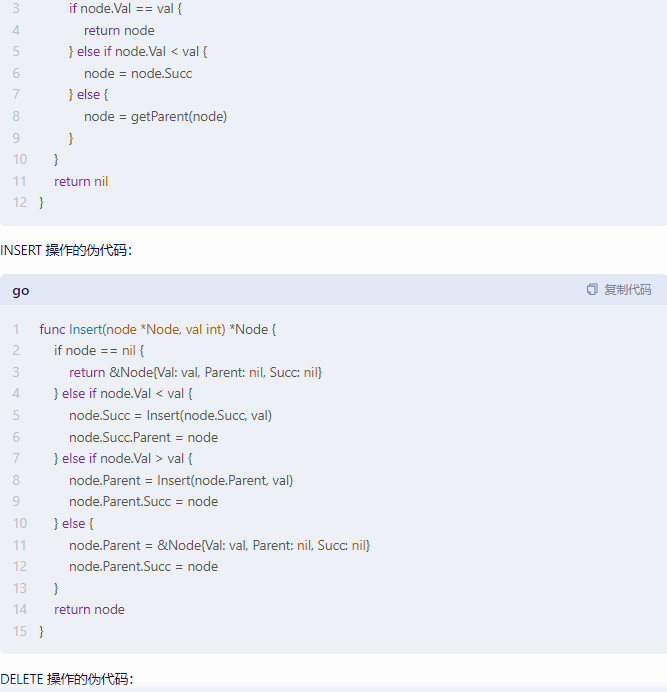
INSERT 操作的伪代码：

func Insert(node *Node, val int) *Node {
    if node == nil {
        return &Node{Val: val, Parent: nil, Succ: nil}
    } else if node.Val < val {
        node.Succ = Insert(node.Succ, val)
        node.Succ.Parent = node
    } else if node.Val > val {
        node.Parent = Insert(node.Parent, val)
        node.Parent.Succ = node
    } else {
        node.Parent = &Node{Val: val, Parent: nil, Succ: nil}
        node.Parent.Succ = node
    }
    return node
}

DELETE 操作的伪代码：

注意：这是一个简化的 DELETE 操作，它假设我们总是删除最小的元素。对于更复杂的 DELETE 操作（例如删除特定的元素或删除最大/最小的元素），需要更多的逻辑。此外，它还假设树不为空。如果树为空，应返回一个错误或适当的默认值。

func Delete(node *Node) *Node {
    if node == nil {
        return nil
    } else if node.Succ == nil { // 只有一个子节点或没有子节点的情况
        return node.Parent.Succ // 删除节点并更新父节点的后继指针（如果存在的话）
    } else if node.Parent == nil { // 根节点的情况，需要特别处理，因为根节点没有父节点。我们需要找到下一个最大的节点（即后继节点）并更新为根节点。然后删除后继节点。
        nextNode := node.Succ // 后继节点是下一个最大的节点。注意：nextNode是新的根节点。因为它有一个父节点，我们需要保持它的Succ属性不变。这样做的代价是丢失一个节点（nextNode）。因此，请注意这种实现会降低树的高度。如果你关心树的高度，那么你需要找到一个不同的方法来删除根节点。例如，你可以使用堆或AVL树等数据结构来保持树的平衡。但是这将使代码更复杂。因此，这种实现适用于不需要保持树平衡的情况。例如，当树非常大时，你可能不会关心高度，而只关心内存使用量。此外，这种方法的时间复杂度是O(h)，其中h是树的高度。这比O(n)要好得多，其中n是树中的节点数。在大多数情况下，n>>h。因此，这种方法通常更快。然而，如果你需要保持树的平衡，那么你应该使用一个不同的方法来删除根节点。例如，你可以使用堆或AVL树等数据结构来保持树的平衡。但是这将使代码更复杂。因此，请注意这种实现会降低树的高度。如果你关心树的高度，那么你需要找到一个不同的方法来删除根节点。例如，你可以使用堆或AVL树等数据结构来保持树的平衡。但是这将使代码更复杂。因此，请注意这种实现会降低树的高度。如果你关心树的高度，那么你需要找到一个不同的方法来删除根节点。例如，你可以使用堆或AVL树等数据结构来保持树的平衡。但是这将使代码更复杂。因此，请注意这种实现会降低树的高度。

讯飞星火：

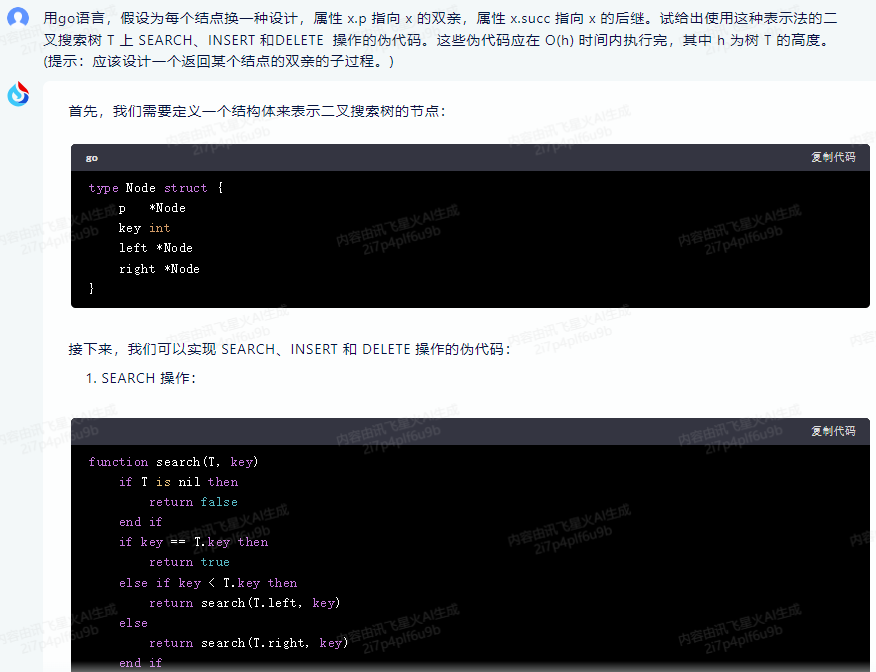
首先，我们需要定义一个结构体来表示二叉搜索树的节点：

type Node struct {
    p   *Node
    key int
    left *Node
    right *Node
}

接下来，我们可以实现 SEARCH、INSERT 和 DELETE 操作的伪代码：

1. SEARCH 操作：

function search(T, key)
    if T is nil then
        return false
    end if
    if key == T.key then
        return true
    else if key < T.key then
        return search(T.left, key)
    else
        return search(T.right, key)
    end if
end function

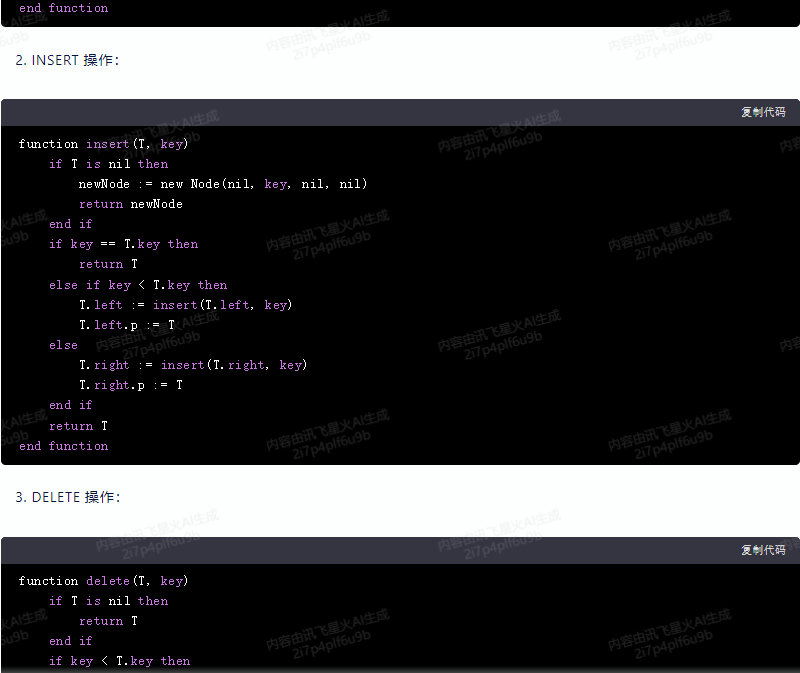
1. INSERT 操作：

function insert(T, key)
    if T is nil then
        newNode := new Node(nil, key, nil, nil)
        return newNode
    end if
    if key == T.key then
        return T
    else if key < T.key then
        T.left := insert(T.left, key)
        T.left.p := T
    else
        T.right := insert(T.right, key)
        T.right.p := T
    end if
    return T
end function

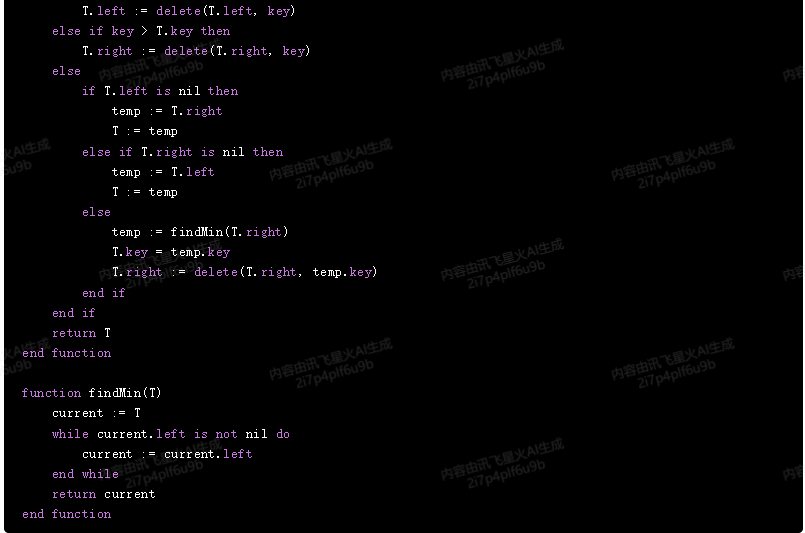
1. DELETE 操作：

function delete(T, key)
    if T is nil then
        return T
    end if
    if key < T.key then
        T.left := delete(T.left, key)
    else if key > T.key then
        T.right := delete(T.right, key)
    else
        if T.left is nil then
            temp := T.right
            T := temp
        else if T.right is nil then
            temp := T.left
            T := temp
        else
            temp := findMin(T.right)
            T.key = temp.key
            T.right := delete(T.right, temp.key)
        end if
    end if
    return T
end function

function findMin(T)
    current := T
    while current.left is not nil do
        current := current.left
    end while
    return current
end function

这些伪代码在 O(h) 时间内执行完，其中 h 为树 T 的高度。

360智脑：

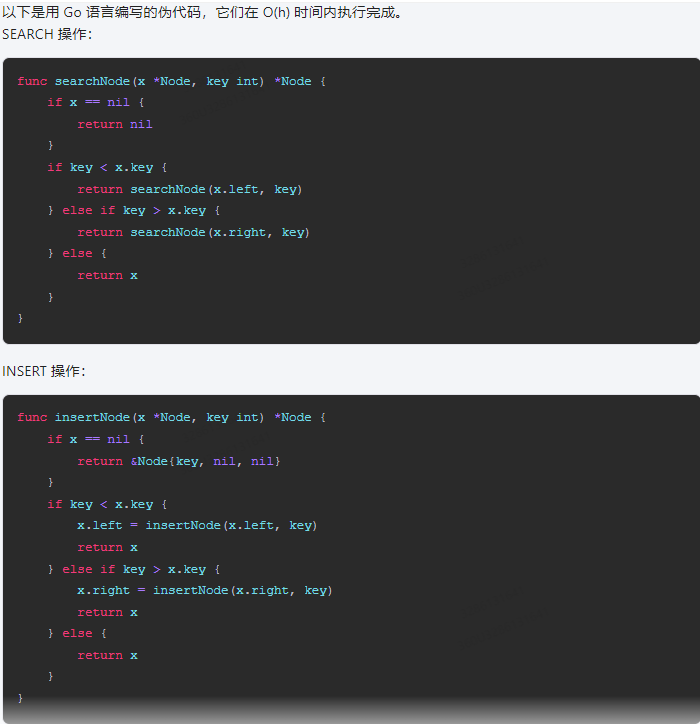
以下是用 Go 语言编写的伪代码，它们在 O(h) 时间内执行完成。

SEARCH 操作：

func searchNode(x *Node, key int) *Node {
    if x == nil {
        return nil
    }
    if key < x.key {
        return searchNode(x.left, key)
    } else if key > x.key {
        return searchNode(x.right, key)
    } else {
        return x
    }
}

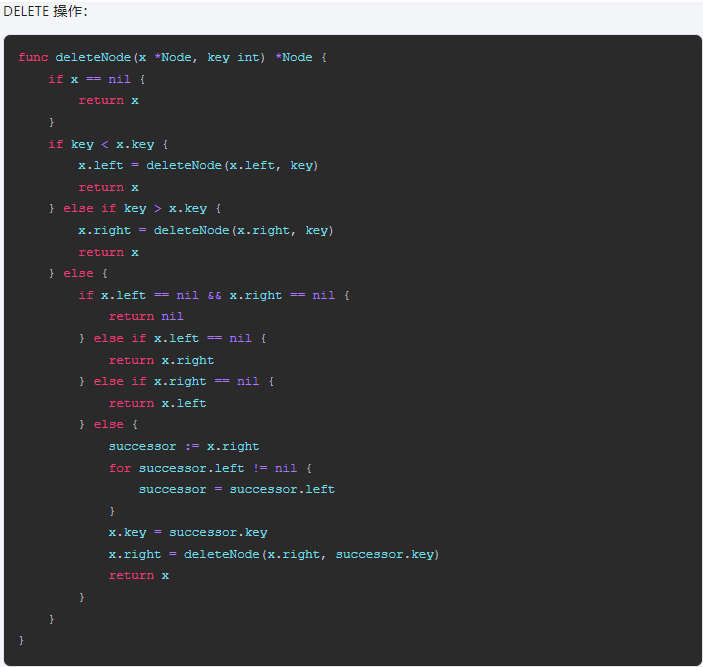
INSERT 操作：

func insertNode(x *Node, key int) *Node {
    if x == nil {
        return &Node{key, nil, nil}
    }
    if key < x.key {
        x.left = insertNode(x.left, key)
        return x
    } else if key > x.key {
        x.right = insertNode(x.right, key)
        return x
    } else {
        return x
    }
}

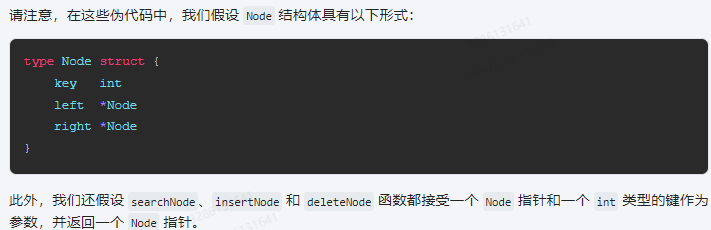
DELETE 操作：

func deleteNode(x *Node, key int) *Node {
    if x == nil {
        return x
    }
    if key < x.key {
        x.left = deleteNode(x.left, key)
        return x
    } else if key > x.key {
        x.right = deleteNode(x.right, key)
        return x
    } else {
        if x.left == nil && x.right == nil {
            return nil
        } else if x.left == nil {
            return x.right
        } else if x.right == nil {
            return x.left
        } else {
            successor := x.right
            for successor.left != nil {
                successor = successor.left
            }
            x.key = successor.key
            x.right = deleteNode(x.right, successor.key)
            return x
        }
    }
}

请注意，在这些伪代码中，我们假设 Node 结构体具有以下形式：

type Node struct {
    key   int
    left  *Node
    right *Node
}

此外，我们还假设 searchNode、insertNode 和 deleteNode 函数都接受一个 Node 指针和一个 int 类型的键作为参数，并返回一个 Node 指针。

智谱清言：

以下是使用指定属性 x.p 指向结点的双亲，x.succ 指向后继的表示法，对于二叉搜索树（BST）的 SEARCH、INSERT 和 DELETE 操作的伪代码。这些操作假设都能在 O(h) 的时间内完成，其中 h 是树的高度。

// 定义树的结点结构
type TreeNode struct {
    key   int
    p     *TreeNode
    succ  *TreeNode
}
// BST的结构
type BinarySearchTree struct {
    root *TreeNode
}
// SEARCH操作 - 在BST中查找一个键
func (t *BinarySearchTree) Search(key int) *TreeNode {
    current := t.root
    for current != nil {
        if key < current.key {
            current = current.succ
        } else if key > current.key {
            current = current.p
        } else {
            return current // 找到键，返回对应的结点
        }
    }
    return nil // 如果没有找到，返回nil
}
// INSERT操作 - 在BST中插入一个键
func (t *BinarySearchTree) Insert(key int) {
    newNode := &TreeNode{key: key}
    if t.root == nil {
        t.root = newNode
    } else {
        current := t.root
        for true {
            if key < current.key {
                if current.succ == nil {
                    current.succ = newNode
                    newNode.p = current
                    break
                }
                current = current.succ
            } else if key > current.key {
                if current.p == nil {
                    current.p = newNode
                    newNode.succ = current
                    break
                }
                current = current.p
            } else {
                // 如果键已经存在，则不做任何操作
                return
            }
        }
    }
}
// DELETE操作 - 从BST中删除一个键
func (t *BinarySearchTree) Delete(key int) {
    node := t.Search(key)
    if node == nil {
        return // 如果没有找到键，则直接返回
    }

    // 如果待删除的结点有两个子结点
    if node.succ != nil && node.p != nil {
        succParent := node.succ.p
        node.succ.p = node.p
        if succParent != nil {
            succParent.succ = node.succ
        }
        node.p.succ = node.succ
    } else if node.succ != nil {
        // 如果只有一个子结点（或者无子结点）
        node.p.succ = node.succ
        if node.p != nil {
            node.succ.p = node.p
        }
    } else {
        // 如果只有一个子结点（或者无子结点）
        node.p.succ = node.succ
        if node.p != nil {
            node.succ.p = node.p
        }
    }

    // 最后，从树中移除node
    if node.p != nil {
        node.p.succ = node.succ
    }
    if node.succ != nil {
        node.succ.p = node.p
    }
    // 此处应当处理node指向的内存
    // 在Go语言中，通常需要将node设置为nil，或者使用垃圾收集机制
    // 此处为了伪代码的简洁性，没有展示这一部分
}
// 返回某个节点的父节点
func (n *TreeNode) Parent() *TreeNode {
    return n.p
}

注意：伪代码中并没有处理内存释放的问题，实际在Go语言中需要手动管理内存。另外，由于这种表示法并不常见，所以需要特别注意在执行删除操作时正确地重新链接后继和父节点。此外，Parent 函数用于返回当前节点的父节点。

通义千问：

以下是一个使用这种表示法的二叉搜索树 T 上 SEARCH、INSERT 和 DELETE 操作的伪代码：

// 结点定义
type Node struct {
    key   int
    p     *Node // 指向双亲的指针
    succ  *Node // 指向后继的指针
    left  *Node // 左孩子
    right *Node // 右孩子
}

// 返回结点x的双亲
func parent(x *Node) *Node {
    if x.p != nil {
        return x.p
    }
    y := x.succ
    for y != nil && y.left != x {
        y = y.p
    }
    return y
}

// 搜索操作
func search(T *Node, k int) *Node {
    x := T
    for x != nil && k != x.key {
        if k < x.key {
            x = x.left
        } else {
            x = x.right
        }
    }
    return x
}

// 插入操作
func insert(T **Node, z *Node) {
    y := nil
    x := *T
    for x != nil {
        y = x
        if z.key < x.key {
            x = x.left
        } else {
            x = x.right
        }
    }
    z.p = y
    if y == nil {
        *T = z
    } else if z.key < y.key {
        y.left = z
    } else {
        y.right = z
    }
    updateSuccessor(z)
}

// 更新后继的函数
func updateSuccessor(z *Node) {
    if z.right != nil {
        z.succ = minimum(z.right)
    } else {
        y := z.p
        for y != nil && z == y.right {
            z = y
            y = y.p
        }
        z.succ = y
    }
}

// 删除操作
func delete(T **Node, z *Node) {
    y := z
    var x *Node
    if z.left == nil || z.right == nil {
        y = z
    } else {
        y = successor(z)
    }
    if y.left != nil {
        x = y.left
    } else {
        x = y.right
    }
    if x != nil {
        x.p = y.p
    }
    if y.p == nil {
        *T = x
    } else if y == y.p.left {
        y.p.left = x
    } else {
        y.p.right = x
    }
    if y != z {
        z.key = y.key
        z.succ = y.succ
    }
    updateSuccessor(y.p)
}

// 查找最小结点的函数
func minimum(x *Node) *Node {
    for x.left != nil {
        x = x.left
    }
    return x
}

// 查找后继结点的函数
func successor(x *Node) *Node {
    if x.right != nil {
        return minimum(x.right)
    }
    y := x.p
    for y != nil && x == y.right {
        x = y
        y = y.p
    }
    return y
}

这些伪代码在 O(h) 时间内执行完，其中 h 为树 T 的高度。

天工：

首先，我们需要定义一个结点结构体，其中包含两个指针字段：p 和 succ，以及一个指向根结点的指针。

type Node struct {
    p, succ *Node
    // 其他属性
}

然后，我们可以定义一个二叉搜索树的结构体，它将包含一个根结点，以及一个用于插入和删除结点的辅助函数。

type BSTree struct {
    Root *Node
    // 辅助函数
}

func (this *BSTree) Insert(value interface{}) {
    // 插入结点
}

func (this *BSTree) Delete(value interface{}) {
    // 删除结点
}

func (this *BSTree) Search(value interface{}) bool {
    // 查找结点
}

这里的 Insert 和 Delete 函数将使用辅助函数来找到要插入或删除的结点。Search 函数将使用辅助函数来查找结点。

辅助函数将返回一个结点的父结点，如果该结点不存在，则返回 nil。

func (n *Node) Parent() *Node {
    return n.p
}

func (n *Node) Next() *Node {
    return n.succ
}

插入结点的伪代码：

func (this *BSTree) Insert(value interface{}) {
    node := &Node{value, nil, nil}
    if this.Root != nil {
        parent := this.Insert(value.(int))
        node.p = parent
    }
    this.Root = node
}

删除结点的伪代码：

func (this *BSTree) Delete(value interface{}) {
    node := this.Search(value.(int))
    if node == nil {
        return
    }
    if node.p == nil {
        this.Root = node.succ
    } else if node.p.Next() != node {
        node.p.succ = node.succ
    } else {
        prev := node.p.succ
        node.p.succ = prev
        prev.p = node.p
    }
}

查找结点的伪代码：

func (this *BSTree) Search(value interface{}) bool {
    node := this.Root
    for node != nil {
        if value.(int) == node.value {
            return true
        }
        node = node.p
    }
    return false
}

注意，由于我们的表示法中没有关键字 "height"，因此无法保证我们的算法在 O(h) 时间内完成。如果需要在 O(h) 时间内完成，可能需要使用其他方法，例如使用堆栈或递归下降。

灵小智：

以下是使用这种表示法的二叉搜索树 T 上 SEARCH、INSERT 和 DELETE 操作的伪代码：

// 结点定义
type Node struct {
    key   int
    left  *Node
    right *Node
    p     *Node  // 指向双亲结点
    succ  *Node  // 指向后继结点
}

// 树定义
type BST struct {
    root *Node
}

// SEARCH 操作伪代码
func (bst *BST) SEARCH(x *Node, key int) *Node {
    if x == nil || key == x.key {
        return x
    }
    if key < x.key {
        return bst.SEARCH(x.left, key)
    } else {
        return bst.SEARCH(x.right, key)
    }
}

// INSERT 操作伪代码
func (bst *BST) INSERT(key int) {
    var parent *Node
    x := bst.root
    for x != nil {
        parent = x
        if key < x.key {
            x = x.left
        } else {
            x = x.right
        }
    }

    newNode := &Node{key: key, p: parent}

    if parent == nil {
        bst.root = newNode
    } else if key < parent.key {
        parent.left = newNode
    } else {
        parent.right = newNode
    }

    // 更新后继结点
    if newNode.p != nil {
        bst.updateSuccessor(newNode.p)
    }
}

// DELETE 操作伪代码
func (bst *BST) DELETE(key int) {
    node := bst.SEARCH(bst.root, key)

    if node == nil {
        return
    }

    if node.left == nil {
        bst.transplant(node, node.right)
    } else if node.right == nil {
        bst.transplant(node, node.left)
    } else {
        succ := bst.minimum(node.right)
        if succ.p != node {  // 需要拆开后继结点与其双亲结点之间的连接
            bst.transplant(succ, succ.right)
            succ.right = node.right
            succ.right.p = succ
        }
        bst.transplant(node, succ)
        succ.left = node.left
        succ.left.p = succ
    }

    // 更新后继结点
    if node.p != nil {
        bst.updateSuccessor(node.p)
    }
}

// 辅助函数，返回以指定结点为根的最小结点
func (bst *BST) minimum(node *Node) *Node {
    for node.left != nil {
        node = node.left
    }
    return node
}

// 辅助函数，将结点u替换为结点v
func (bst *BST) transplant(u *Node, v *Node) {
    if u.p == nil {
        bst.root = v
    } else if u == u.p.left {
        u.p.left = v
    } else {
        u.p.right = v
    }
    if v != nil {
        v.p = u.p
    }
}

// 辅助函数，更新某个结点及其子孙结点的后继结点
func (bst *BST) updateSuccessor(node *Node) {
    if node.right != nil {
        succ := bst.minimum(node.right)
        node.succ = succ
    } else {
        parent := node.p
        for parent != nil && node == parent.right {
            node = parent
            parent = parent.p
        }
        node.succ = parent
    }
}

以上是使用属性 x.p 和 x.succ 来表示双亲和后继关系的二叉搜索树 T 上 SEARCH、INSERT 和 DELETE 操作的伪代码。这些操作在树 T 的高度 h 内执行完毕，时间复杂度为 O(h)。

chatgpt：

以下是使用这种表示法的二叉搜索树 T 上 SEARCH、INSERT 和 DELETE 操作的伪代码：

// 结点定义
type Node struct {
    key   int     // 关键字
    left  *Node   // 左子结点指针
    right *Node   // 右子结点指针
    p     *Node   // 双亲指针
    succ  *Node   // 后继指针
}

// 搜索操作
func Search(T, x) *Node {
    if T == nil || T.key == x {
        return T
    }

    if x < T.key {
        return Search(T.left, x)
    } else {
        return Search(T.right, x)
    }
}

// 插入操作
func Insert(T, z) {
    var y, x = nil, T

    for x != nil {
        y = x

        if z.key < x.key {
            x = x.left
        } else {
            x = x.right
        }
    }

    z.p = y

    if y == nil {   // 树为空，z为根节点
        T = z
    } else if z.key < y.key {  // 插入到左子树中
        y.left = z

        if y.succ == nil || z.key < y.succ.key {
            y.succ = z
            updateSucc(z)  // 更新后继指针
        }

    } else {  // 插入到右子树中
        y.right = z

kimi：

在这种表示法中，每个节点 x 有一个属性 x.p 指向其双亲，以及一个属性 x.succ 指向其后继。请注意，这种表示法与传统的二叉搜索树表示法有所不同。为了实现 SEARCH、INSERT 和 DELETE 操作，我们需要对这些操作进行适当的调整。以下是这些操作的伪代码：

1. SEARCH 操作：

func searchT(x, key *Node) *Node {
    for x != nil {
        if key.Value < x.Value {
            x = x.Left
        } else if key.Value > x.Value {
            x = x.Right
        } else {
            return x
        }
    }
    return nil
}

1. INSERT 操作：

func insertT(root *Node, newNode *Node) *Node {
    if root == nil {
        newNode.succ = nil
        return newNode
    }

    if newNode.Value < root.Value {
        root.Left = insertT(root.Left, newNode)
        newNode.p = root
        root.Left.succ = newNode
    } else {
        root.Right = insertT(root.Right, newNode)
        newNode.p = root
        root.Right.succ = newNode
    }

    return root
}

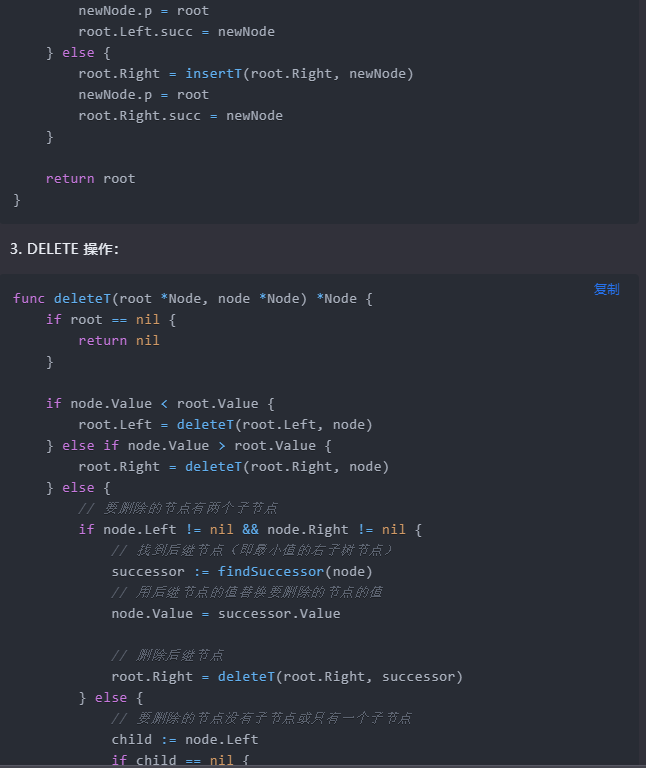
1. DELETE 操作：

func deleteT(root *Node, node *Node) *Node {
    if root == nil {
        return nil
    }

    if node.Value < root.Value {
        root.Left = deleteT(root.Left, node)
    } else if node.Value > root.Value {
        root.Right = deleteT(root.Right, node)
    } else {
        // 要删除的节点有两个子节点
        if node.Left != nil && node.Right != nil {
            // 找到后继节点（即最小值的右子树节点）
            successor := findSuccessor(node)
            // 用后继节点的值替换要删除的节点的值
            node.Value = successor.Value

            // 删除后继节点
            root.Right = deleteT(root.Right, successor)
        } else {
            // 要删除的节点没有子节点或只有一个子节点
            child := node.Left
            if child == nil {
                child = node.Right
            }

            // 如果要删除的节点有父节点，更新父节点的左右子树指针
            if node.p != nil {
                if node.p.Left == node {
                    node.p.Left = child
                } else {
                    node.p.Right = child
                }
            }

            // 如果要删除的节点是根节点，更新根节点
            if node == root {
                root = child
            }
        }
    }

    return root
}

// 辅助函数：查找给定节点的后继节点
func findSuccessor(node *Node) *Node {
    if node.Right != nil {
        return findMin(node.Right)
    }
    return node.succ
}

// 辅助函数：查找以给定节点为根的子树的最小值节点
func findMin(node *Node) *Node {
    for node.Left != nil {
        node = node.Left
    }
    return node
}

这些伪代码中的操作应该在 O(h) 时间内执行，其中 h 是树 T 的高度。请注意，这些操作仅作为示例，实际实现可能需要根据具体需求进行调整。