【LeetCode贪心#10】划分字母区间（有涉及hash数组的使用）

划分字母区间

力扣题目链接(opens new window)

字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。

示例：

输入：S = "ababcbacadefegdehijhklij"
输出：[9,7,8] 解释：划分结果为 "ababcbaca", "defegde", "hijhklij"。每个字母最多出现在一个片段中。像 "ababcbacadefegde", "hijhklij" 的划分是错误的，因为划分的片段数较少。

提示：

S的长度在[1, 500]之间。
S只包含小写字母 'a' 到 'z' 。

思路

题目分析

题目是什么意思呢？拿示例来说

当前输入为：S = "ababcbacadefegdehijhklij"

ababcbacadefegdehijhklij

↑

此时遍历字符串，取到子串'a'，那么S中的所有'a'都要包含到当前子串中，于是继续往后遍历

ababcbacadefegdehijhklij

 ↑

此时又取到'b',同理S中的所有'b'都要包含到当前子串中，当前子串为"ab"

以此类推，当遍历一段时间后，可以划分出第一个片段，即"ababcbaca"

ababcbacadefegdehijhklij

        ↑

记录字符出现位置

上述过程中一个核心问题是：如何确定当前字母在字符串中的最远位置

只有解决这个问题才能获取片段的结束位置

这里通过哈希表的方式来解决（此技巧在有效的字母异位词也出现过）

定义一个hash数组 int hash[27] = {0}，有26个字母，所以数组大小设为27就很够了

然后遍历字符串S

int hash[27] = {0}；

for(int i = 0; i < S.size(); ++i){

}

同时，记录当前遍历所得的字符的位置

int hash[27] = {0}；

for(int i = 0; i < S.size(); ++i){

    hash[S[i] - 'a'] = i;//

}

S[i]是当前字符，通过S[i] - 'a'确定其是第几个字母，并得到其在hash数组中的具体位置

然后再hash数组中记录当前遍历过程中S[i]在S中出现的位置 i

例如：第一个遍历得到的字符是'b'，此时可以定位到其位于hash数组中的下标1 位置（看做字母表的话就是第二个）

i 代表着'b'目前在S中的第 i 个位置出现，记录下来即可

通过遍历过程的不断推进，hash数组会记录下某个字符最后一次在S中出现的位置，这便是最远位置

由上述方法我们就可以记录任意26个字母在某个字符串中出现过的最远位置

切片

在代码实现时，我们会先遍历一遍S，将每个字符在S中的最远位置求出来记录于hash数组

此时，我们再次遍历S，设置左右边界，在遍历过程中不断更新右边界

直到当前遍历下标i与右边界相等，此时意味着我们已经找到分割位置，然后可以将结果保存（结果为分割子串的长度，因此只需保存左右边界的作差结果即可）

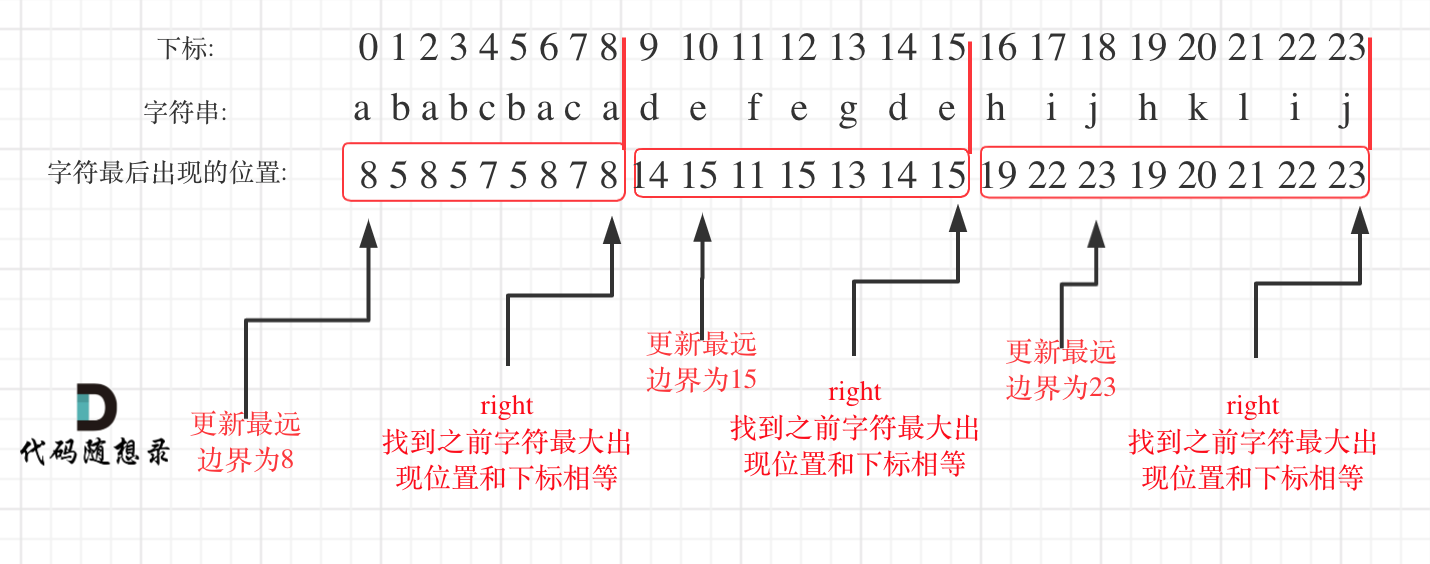
借用一下卡哥的图

如图，第一次遍历完S之后得到hash数组，由该数组显示S的第一个字符'a'最后一次出现位置是下标8 处

当第二次遍历S时，使用遍历下标 i 为hash数组的索引，不断地取当前遍历字符的最远出现位置来更新右边界right

而更新时只用最大值来更新，因为'a'的最远位置是8，可以看到"ababcbaca"中没有哪个字符的位置比8要远，因此右边界就一直指向8

那么，当i == right时，我们就计算并保存"ababcbaca"的长度，即right - left + 1

for (int i = 0; i < S.size(); i++) {

    right = max(right, hash[S[i] - 'a']); // 找到字符出现的最远边界

    if (i == right) {

       result.push_back(right - left + 1);

       left = i + 1;

    }

}

代码

根据上面的分析，得到步骤如下：

1、创建一个hash数组（需要记录某个字符出现的最远位置作为分割依据）

2、遍历目标字符串，记录每个字符出现的最远位置

3、定义左右边界遍历与结果变量

4、再次遍历字符串，使用下标i去hash数组中找当前遍历字符的最远距离，不断更新右边界right

5、当i == right，记录结果

class Solution {

public:

    vector<int> partitionLabels(string s) {

        //定义hash数组，记录每个字符的最远位置

        int hash[27] = {0};

        for(int i = 0; i < s.size(); ++i){//获取每个字符的最远位置

            hash[s[i] - 'a'] = i;//记录当前字母在s中出现的位置i

        }

        vector<int> res;

        int left = 0;//定义左右边界

        int right = 0;

        for(int i = 0; i < s.size(); ++i){

            //取hash中的最大值更新right

            right = max(hash[s[i] - 'a'], right);

            if(i == right){

                res.push_back(right - left + 1);

                left = i + 1;//记录一个片段后更新左边界

            }

        }

        return res;

    }

};

注意点：

在 C++ 中，int a, b = 0 表示定义了两个整型变量 a 和 b，其中 b 被初始化为 0，而 a 没有被初始化，其值是未定义的。这种语法是 C++ 中的变量声明的一种简写方式，但容易造成误解，应尽量避免使用。

而 int a = 0; int b = 0; 则表示定义了两个整型变量 a 和 b，它们都被初始化为 0。这种写法更加明确，不会造成误解，建议优先使用。

因此，这两种写法的区别在于变量初始化的方式和是否对变量进行了初始化。在编写代码时，应该尽量避免使用第一种写法，而是采用第二种写法进行变量定义和初始化。