代码随想录算法训练营Day2|977有序数组的平方 209.长度最小的子数组 59螺旋矩阵Ⅱ（C++）

LeetCode刷题，代码随想录算法训练营Day2

977.有序数组的平方

题目链接 : 977.有序数组的平方

题目思路：关键在于双指针思想的应用

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

暴力破解（sort方法、冒泡）

应该为一个for循环进行全部平方，直接调用sort进行排序即可，时间复杂度n+n*log2n

 1 class Solution {
 2 public:
 3     vector<int> sortedSquares(vector<int>& nums) {
 4         int i;
 5         for(i=0;i<nums.size();i++){
 6             nums[i]*=nums[i];
 7         }
 8         sort(nums.begin(),nums.end());
 9         return nums;
10     }
11 };

如果使用冒泡排序时间复杂度会为n²

1  for(i=0;i<nums.size()-1;i++){
2       for(j=0;j<nums.size()-1-i;j++){
3             if(nums[j]>nums[j+1]){
4                     swap(nums[j],nums[j+1]);
5             }
6      }
7 }

双指针法

和昨天的题目一样，通过双指针在一个for循环里做出两个for循环的事情。本题通过一前一后的双指针相向进行

如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。

如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。

 1 class Solution {
 2 public:
 3     vector<int> sortedSquares(vector<int>& A) {
 4         int k = A.size() - 1;  //索引的下标
 5         vector<int> result(A.size(), 0);//定义新数组
 6         for (int i = 0, j = A.size() - 1; i <= j;) { //循环终止， 注意这里要i <= j，因为最后要处理两个元素
 7             if (A[i] * A[i] < A[j] * A[j])  {
 8                 result[k--] = A[j] * A[j];
 9                 j--;
10             }
11             else {
12                 result[k--] = A[i] * A[i];
13                 i++;
14             }
15         }
16         return result;
17     }
18 };

注意：不能再i=j的时候退出，否则中间两个无法比较。

由于i++和j--是有条件的，因此for循环的最后需要空着，自增自减在条件中进行完成。

209.长度最小的子数组

题目链接：209.长度最小的子数组

解题思路：

暴力解法

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int result = INT32_MAX; // 最终的结果
        int sum = 0; // 子序列的数值之和
        int subLength = 0; // 子序列的长度
        for (int i = 0; i < nums.size(); i++) { // 设置子序列起点为i
            sum = 0;
            for (int j = i; j < nums.size(); j++) { // 设置子序列终止位置为j
                sum += nums[j];
                if (sum >= s) { // 一旦发现子序列和超过了s，更新result
                    subLength = j - i + 1; // 取子序列的长度
                    result = result < subLength ? result : subLength;
                    break; // 因为我们是找符合条件最短的子序列，所以一旦符合条件就break
                }
            }
        }
        // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }
};

时间复杂度O（n²）

滑动窗口解法

滑动窗口即不断通过调节子序列的起始位置和最终位置，得出想要的结果

下标j应该为滑动窗口的终止位置。如果j是位于起始位置，则仍然是暴力解法。

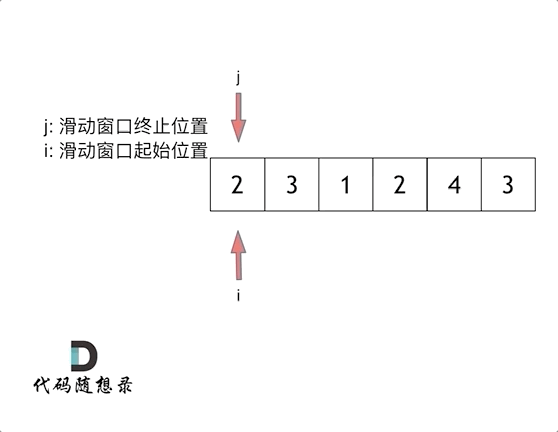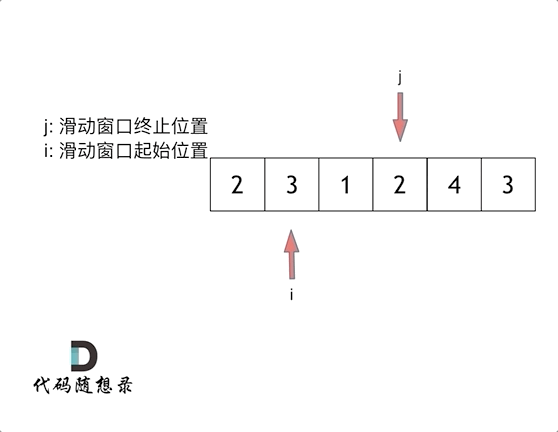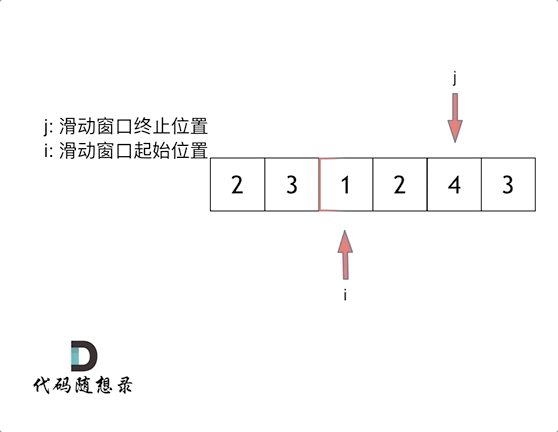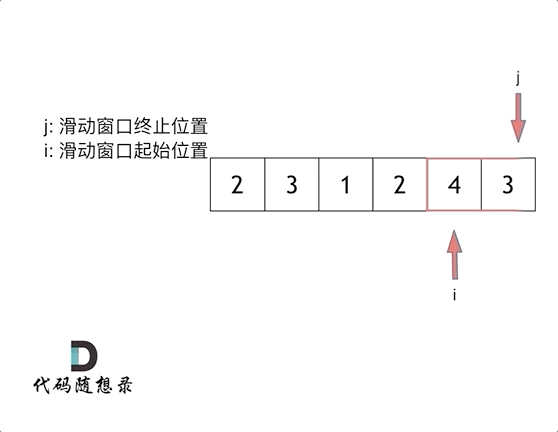
当集合里的所有元素和大于s时再移动起始位置即可

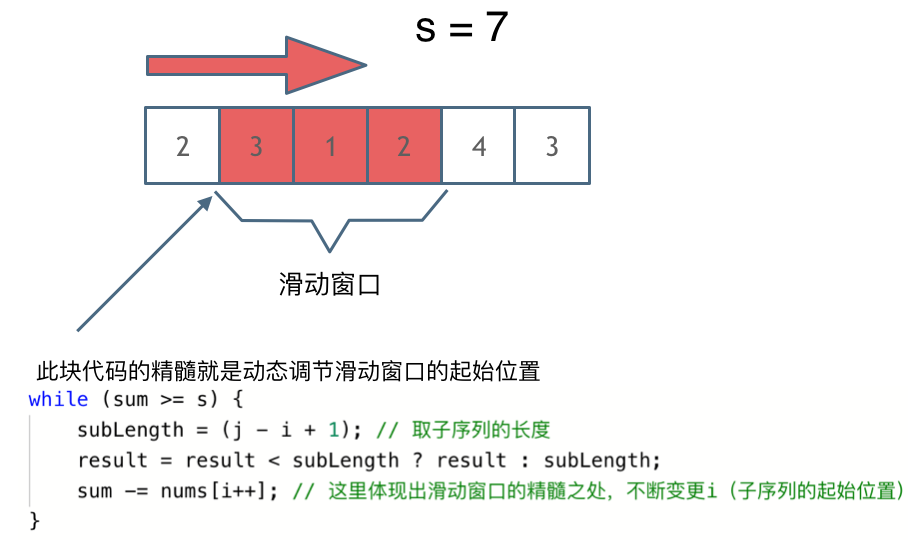
可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。

代码实现：

 1 class Solution {
 2 public:
 3     int minSubArrayLen(int s, vector<int>& nums) {
 4         int result = INT32_MAX;
 5         int sum = 0; // 滑动窗口数值之和
 6         int i = 0; // 滑动窗口起始位置
 7         int subLength = 0; // 滑动窗口的长度
 8         for (int j = 0; j < nums.size(); j++) {
 9             sum += nums[j];
10             // 注意这里使用while，每次更新 i（起始位置），并不断比较子序列是否符合条件
11             while (sum >= s) {
12                 subLength = (j - i + 1); // 取子序列的长度
13                 result = result < subLength ? result : subLength;
14                 sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处，不断变更i（子序列的起始位置）
15             }
16         }
17         // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
18         return result == INT32_MAX ? 0 : result;
19     }
20 };

59螺旋矩阵Ⅱ

题目链接：59螺旋矩阵Ⅱ

模拟解法

螺旋矩阵没有暴力破解，只能通过四个for循环重复实现对不同数字的输入。螺旋矩阵的重要点在于判断最后一个列的数字个数和奇数大小矩阵时的中间位置的数字。

整个矩阵的实现是由两组循环实现的，最外层是while循环，用来控制一周的整体循环，每一行通过一个for循环实现一行内的输入输出。

处理规则：循环不变量

按左闭右开的规则对各边进行遍历，都只处理第一个节点，最后一个节点不处理。

定义的i对应startx，j对应starty，二维数组中i控制行的数量，j控制列的数量，因此第一个for中就是只对j进行修改。外层修改完成后startx和starty都进行自增，内一层初始的节点位置沿对角线进行逐层深入。

每层长度通过offset进行控制，最外层就是1，每往内一层即+1

螺旋矩阵的数字输入通过count进行计数，在每个for循环内都要自增一次

 1 class Solution {
 2 public:
 3     vector<vector<int>> generateMatrix(int n) {
 4         vector<vector<int>> res(n, vector<int>(n, 0));//使用vector定义二维数组
 5         int startx=0,starty=0;//定义循环一个圈的起始位置
 6         short loop=n/2;//n==3时一次循环，n==4时2次循环完成
 7         short mid=n/2;//中间的部分单独填充，位于中心位置
 8         short count=1;//定义矩阵中每一个空格赋值,从1开始
 9         short offset=1;//需要控制每一个边遍历的长度，每循环一次右边界收缩一位
10         short i,j;
11         while(loop--){
12             i=startx;
13             j=starty;
14             //四个for模拟转了一圈
15             //模拟填充上行从左到右（左闭右开）//x不变，j变化
16             for(j=starty;j<n-offset;j++){
17                 res[startx][j]=count++;
18             }
19             //模拟填充右列从上到下
20             for(i=startx;i<n-offset;i++){
21                 res[i][j]=count++;
22             }
23              //模拟填充下行从右到左
24             for(;j>starty;j--){
25                 res[i][j]=count++;
26             }
27             for(;i>startx;i--){
28                 res[i][j]=count++;
29             }
30             startx++;
31             starty++;//xy沿对角线向内移动
32             offset+=1;//offset控制每一圈里一条边遍历的长度
33         }
34         //n是奇数的话，需单独为中间的数赋值
35         if(n%2){
36             res[mid][mid]=count;
37         }
38         return res;
39     }
40 };

总结

除最后一个题目外，其他的数组题目都是对双指针思想的应用，双指针是通过指针的移动实现对一次for循环的取代，从而节约和降低时间复杂度。

由于之前没有学习过C++，现在用C++写代码有很多知识点还是比较难以理解的，现在虽然很吃力，但只要坚持就一定可以克服，加油！