stm32启动文件ld md hd cl vl xl分析及选择

startup_stm32f10x_cl.s
互联型的STM32F105xx，STM32F107xx
startup_stm32f10x_hd.s 大容量的STM32F101xx，STM32F102xx，STM32F103xx
startup_stm32f10x_hd_vl.s 大容量的STM32F100xx
startup_stm32f10x_ld.s 小容量的STM32F101xx，STM32F102xx，STM32F103xx
startup_stm32f10x_ld_vl.s 小容量的STM32F100xx
startup_stm32f10x_md.s 中容量的STM32F101xx，STM32F102xx，STM32F103xx
startup_stm32f10x_md_vl.s 中容量的STM32F100xx
startup_stm32f10x_xl.s 超大容量FLASH在512K到1024K字节的STM32F101xx，STM32F102xx，STM32F103xx

疑问一：为什么需要选择启动文件？

1.建立中断服务入口地址，即把中断向量与中断服务函数链接起来。

我们知道在串口NVIC配置中我们只定义了个    NVIC_InitStructure.NVIC_IRQChannel = USART2_IRQn;

也就是中断服务向量，再然后我们在stm32f10x_it.c文件的void USART2_IRQHandler(void){} 函数里添加串口的服务程序。

但是mcu怎么知道中断向量USART2_IRQn对应的是USART2_IRQHandler(){}呢，这个就是启动文件所起的作用。

在启动文件   .s  中 以   g_pfnVectors:  开头。

2.从systeminit()函数进入到main()函数.

对于stm32我们定义系统时钟的时候直接在system_stm3210x.c文件里修改宏定义即可，而事实上到底是从哪开始执行的呢？

system_stm3210x.c文件里有个SystemInit()函数，就是对时钟的设置。

而这个SystemInit()在哪调用的呢，就是启动文件先调用了，然后才进入到mian()函数。

在启动文件  .s  中有以下一段话可以解释。

/* Call
the clock system intitialization function.*/

bl  SystemInit

/* Call static constructors */

bl __libc_init_array

/* Call the application's entry point.*/

bl main

bx lr
3．有些启动文件定义了堆栈大小，可以在这里进行修改。（有些是在  ．ld  进行定义的）

疑问二：这些文件在哪里？

打开官方库文件，可以了解到STM32F10x_StdPeriph_lib/Libraries/CMSIS/CM3/DeviceSupport/ST/STM32F10x/startup

下有4个文件夹arm  gcc_ride7  iar  TrueSTUDIO

到底选择哪个文件夹呢？  这与编译器有关，不同的编译器调用的指令集是不同的，所以需谨慎选择

arm适用于arm编译器   gcc_ride7适用基于GCC_ride7编译器的  iar就不用说了都清除  TrueSTDIO是ST自己的编译器当然也是基于GCC的用MDK于eclipse可以使用

(在eclipse下用的GCC插件的话，需要把后缀名 .s 改为 .S成大写，不然会编译出错)

疑问三：怎么选择101xx 102xx 103xx是小容量、中容量还是大容量？

查user manual手册，以下为摘录

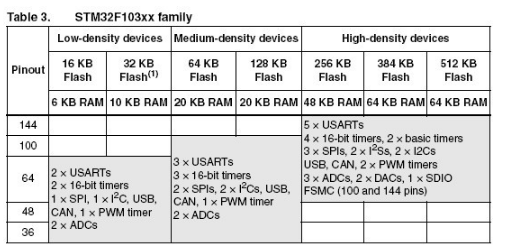
可以这么认为：flash容量<=32k       选择  ld

64k<=   <=128k     选择 md

256<=   <=512k     选择  hd

那怎么区分MCU是多大的flash容量呢？

可以参考下表对于芯片命名说明：Flash memory size

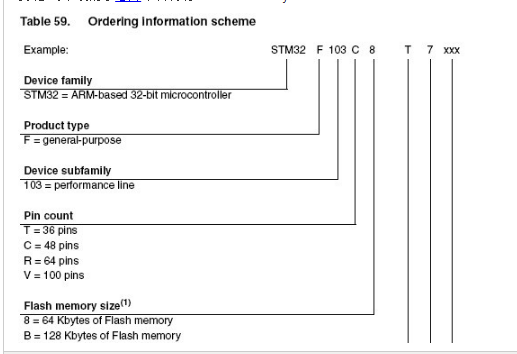
6：32K 8：64K
B：128K C：256K
D：384K E：512K  Flash memory size!