斜率优化初探：以 [HNOI2008]玩具装箱为例

题目传送门

记 $f[i]$ 表示装好前 $i$ 个的最小花费。容易写出转移：

\[f[i] = \min_{j \lt i} \ [f[j]+(s[i] - s[j] - 1 - L) ^ 2]
\]

直接转移是 $O(n ^ 2)$ 的，我们考虑斜率优化。

斜率优化的过程

（一）问题转化成了求最小截距。

我们把 $min$ 的外壳去掉，并且提前把 $L +1$ （式子更简洁）可以得到：

\[f[i] = f[j]+(s[i] - s[j] - 1 - L) ^ 2
\]

把括号打开，可以得到：

\[f[i] = f[j] + s[i] ^ 2 - 2\times s[i] \times L - 2 \times s[i] \times s[j] + (s[j] + L) ^ 2
\]

移项后得到：

\[(2s[i]) \times s[j] + (f[i] - s[i] ^ 2 + 2 \times s[i] \times L) = f[j] + (s[j] +L) ^ 2
\]

此时，如果我们把这看做一个一次函数，那么

\[k = 2s[i]\\
x = s[j]\\
b = (f[i] - s[i] ^ 2 + 2 \times s[i] \times L)\\
y = f[j] + (s[j] +L) ^ 2
\]

注意到固定 $i$ 后，$k$ 是固定的。而对于每个 $j$，我们都可求出对应的 $(x, y)$。此时当 $b$ 最小时，$f[i]$ 也会最小。

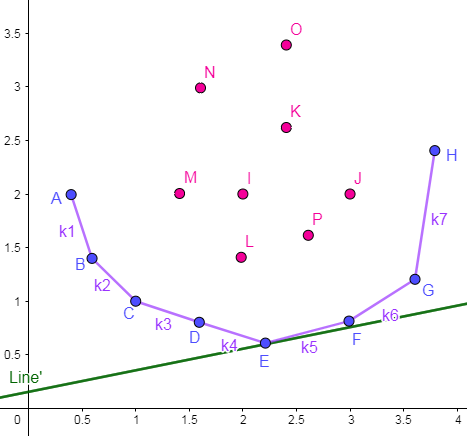
（二）截距在哪里最小？（图像理解）

我们知道有用的 $j$ 在二维平面上形成的点阵是个凸包。

我们惊讶的发现斜率竟然是固定的！我们可以平移这条直线至与凸包相切，显然这个切点 $E$，就对应着最小的截距。

怎么找这个点呢？发现 $E$ 点以前的斜率都小于当前 $k$， $E$ 点之后的斜率都大于等于 $k$，因此可以二分这个位置。时间复杂度 $O(nlogn)$。

（三）决策单调性的优化（图像理解）

决策单调性的定义：

设 $j_0[i]$ 表示 $f[i]$ 转移的最优决策点，那么 决策单调性 可以描述为 $\forall i \le i'$， $j_0[i] \le j_0[i']$。即随着 $i$ 递增，所找到的 最优决策点 是递增态（非严格递增）。

发现 $k = 2s[i]$，而 $s[i]$ 是前缀和，显然是递增的，那么我们的决策点也一定会越来越大（因为目标斜率递增）

详细证明参见参考博客。

用单调队列维护凸包的点集，分三步：

将斜率比目标斜率小的点弹出，在队首位置找到最优决策点 $j$。
用最优决策点 $j$ 更新 $dp[i]$。
把新的点加入队列中。

时间复杂度 $O(n)$。

#include<bits/stdc++.h>

#define F(i,l,r) for(int i(l);i<=(r);++i)

#define G(i,r,l) for(int i(r);i>=(l);--i)

#define int ll

using namespace std;

using ll = long long;

const int N = 1e5 + 5;

int L, n, h = 1, t = 0;

int f[N], s[N], q[N];

int X(int j){

	return s[j] +L;

}

int Y(int j){

	return f[j] + (s[j] + L) * (s[j] + L);

}

long double slope(int i, int j){

	return (long double)(Y(i) - Y(j)) / (long double)(X(i) - X(j));

}

signed main(){

	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);

	cin >> n >> L;

	++L;

	F(i, 1, n) cin >> s[i], s[i] += s[i - 1] + 1;

	q[++t] = 0;

	F(i, 1, n){

		while(h < t && slope(q[h], q[h + 1]) < 2 * s[i]) ++ h;

		int j = q[h];

		f[i] = f[j] + (s[i] - s[j] - L) * (s[i] - s[j] - L);

		while(h < t && slope(q[t - 1], q[t]) > slope(q[t - 1], i)) -- t;

		q[++ t] = i;

	}

	cout << f[n] << '\n';

	return 0;

}

反思：移项的依据

为了用 $Function(i)$ 表示出 $Function(j)$，我们把含 $i$ 的东西移到等式左边，把含 $j$ 的东西移到等式右边。以此整理出 "不变的 $k$，待求解的 $b$，确定的 $x, y$"。记得 $f[i]$ 一定要放在截距 $b$ 里面！因为我们是对截距求解极值。

注意 $k, x, y$ 都是确定的，只有 $b$ 是待定的。

参考博客：

【学习笔记】动态规划—斜率优化DP（超详细） - 辰星凌 - 博客园 (cnblogs.com)