MongoDB 简单介绍

MongoDB介绍

疑问	解答
什么是 MongoDB	一个以 JSON 为数据模型的文档数据库
为什么叫文档数据库？	文档来自于 “JSON Document”，并非我们一般理解的 PDF，WORD 文档
谁开发 MongDB？	上市公司 MongoDB Inc. ，总部位于美国纽约。
主要用途	应用数据库，类似于 Oracle，MySQL 海量数据处理，数据中台
主要特点	建模为可选 JSON 数据模型比较适合开发者 横向扩展可以支撑很大数据量和并发
MongoDB 是免费的吗？	MongoDB 有两个发布版本：社区版和企业版。 社区版是基于 SSPL，一种和 AGPL 基本类似的开源协议 企业版是基于商业协议，需付费使用

MongoDB VS 关系型数据库

	MongoDB	RDBMS
数据模型	文档模型	关系模型
数据库类型	OLTP	OLTP
CURL 操作	MQL/SQL	SQL
高可用	复制集	集群模式
横向扩展能力	通过原生分片完善支持	数据分区或者应用侵入式
索引支持	B-树、全文索引、地理位置索引、多键(multikey)索引、TTL索引	B 树
开发难度	容易	困难
数据容量	没有理论上限	千万、亿
扩展方式	垂直扩展+水平扩展	垂直扩展

MongoDB 优势：面向开发者的易用+高效数据库

• 简单直观：以自然的方式来建模，以直观的方式来与数据库交互
• 结构灵活：弹性模式从容响应需求的频繁变化
• 原生的高可用
  • Replica Set - 2 to 50 个成员
  • 自恢复
  • 多中心容灾能力
  • 滚动服务 - 最小化服务终端
• 横向扩展能力
  • 需要的时候无缝扩展
  • 应用全透明
  • 多种数据分布策略
  • 轻松支持 TB - PB 数量级
• 快速开发：做更多的事，写更少的代码
  • 数据库引擎只需要在一个存储区读写
  • 反范式、无关联的组织极大优化查询速度
  • 程序 API 自然，开发快速

灵活：快速响应业务变化

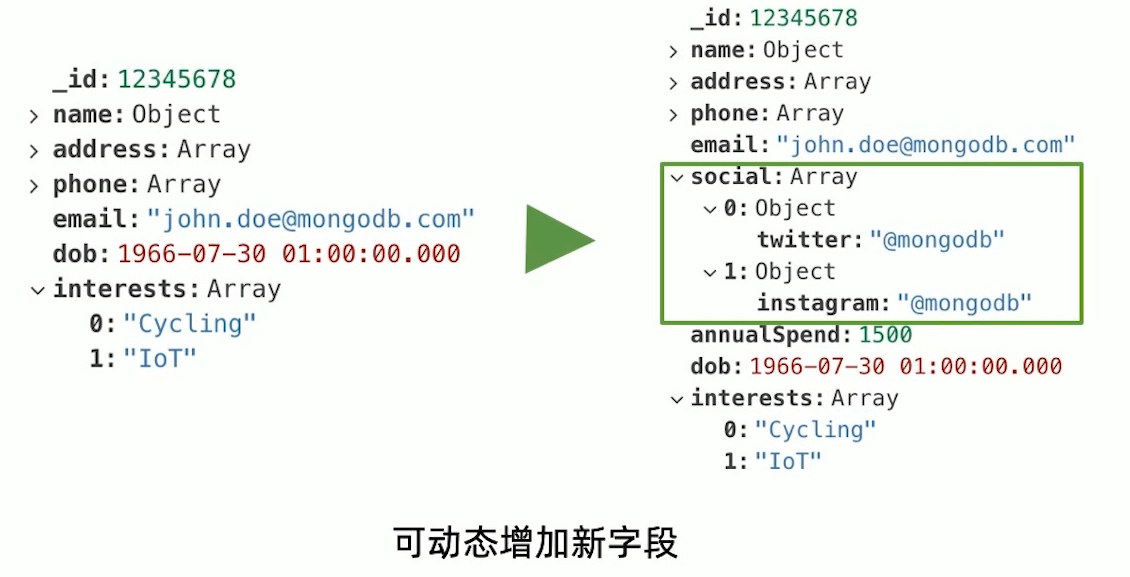
• 多形性：同一个集合中可以包含不同字段（类型）的文档对象
• 动态性：线上修改数据模式，修改是应用与数据库均无须下线
• 数据治理：支持使用 JSON Schema 来规范数据模式。在保证模式灵活动态的前提下，提供数据治理能力。

MongoDB 技术优势总结

• JSON 结构和对象模型接近，开发代码量低
• JSON 的动态模型意味着更容易响应新的业务需求
• 复制集提供 99.999% 高可用
• 分片架构支持海量数据和无缝扩容

MongoDB 全家桶

软件模块	描述
mongod	MongoDB 数据库软件
mongo	MongoDB 命令行工具，管理 MongoDB数据库
mongodump/mongorestore	MongoDB路由进程，分片环境下使用
mongoexport/mongoimport	命令行数据库备份与恢复工具
Compass	MongoDB GUI 管理工具
Ops Manager（企业版）	MongoDB 集群管理软件
BI Connector（企业版）	SQL解释器/BI套接件
MongoDB Charts（企业版）	MongoDB 可视化软件
Atlas（付费及免费）	MongoDB 云托管服务，包括永久免费云数据库

MongoDB 模型设计基础

数据模型大的三要素

• 实体
• 属性
• 关系

数据模型的三层深度

• 概念模型
• 逻辑模型
• 物理模型

一个模型逐步细化的过程