【MOOC】华中科技大学计算机组成原理慕课答案-第三章-运算方法与运算器

待整理。

单选

1　原码除法是指
A. 操作数用绝对值表示，加上符号位后相除
√B. 操作数取绝对值相除，符号位单独处理
C. 操作数用原码表示，然后相除
D. 操作数用补码表示并进行除法，但商用原码表示

2　单符号位补码表示的两个同号数相加或异号数相减时，所得结果的符号位SF和进位标志CF进行（ ）运算为1时，表示运算的结果产生溢出
A. 与
√B. 异或
C. 或
D. 与非

3　在定点二进制运算器中，减法运算一般通过______来实现
A. 原码运算的二进制减法器
B. 补码运算的二进制减法器
C. 反码运算的二进制加法器
√D. 补码运算的二进制加法器

4　浮点数加减运算过程一般包括对阶、尾数运算、规格化、舍入和判溢出等步骤。设浮点数的阶码和尾数均采用补码表示，且位数分别为5位和7位（均包含2位符号位）。若有两个数X = 2＾7 × 29/32 ,Y= 2＾5 × 5/8，则用浮点加法计算X+Y 的最终结果是
√A. 溢出
B. 00111 0100010
C. 00111 1100010
D. 01000 0010001

摘自MOOC第三章3.7视频。


对阶时，小阶向大阶看齐。本题发生阶码上溢。

5　若浮点数用补码表示，则判断运算结果是否为规格化数的方法是
A. 数符与尾数小数点后第一位数字相同
B. 阶符与数符相同
C. 阶符与数符相异
√D. 数符与尾数小数点后第一位数字相异

6　在下列浮点数表示中，左移一位就可被规格化浮点数是
√A.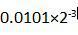

B.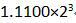

C.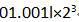

D.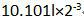

7　以下各机器数中，引入___数据表示可消除减法操作
A. 移码
B. 原码
C. 反码
√D. 补码

8　设机器数字长8位(含1位符号位)，若机器数DAH为补码，分别对其进行算术左移一位和算术右移一位，其结果分别为
A. B4H，6DH
B. B5H，6DH
C. B5H，EDH
√D. B4H，EDH

9　已知A=0.1011,B= -0.0101，则[A+B]补 为
√A. 0.0110
B. 1.0110
C. 0.1101
D. 1.1011

10　下列说法错误的是
A. 运算器中通常都有一个状态标记寄存器，为计算机提供判断条件，以实现程序转移
B. 在小数除法中，为了避免溢出，要求被除数的绝对值小于除数的绝对值
C. 并行加法器中虽然不存在进位的串行传递，但高位的进位依然依赖于数据的低位
√D. 补码乘法器中，被乘数和乘数的符号都不参加运算

11　以下关于ALU的描述正确的是
A. 只能完成逻辑运算
B. 只能完成算术运算
C. 不能支持乘法运算
√D. 能完成算术与逻辑运算

12　在计算机中，对于正数，其三种机器数右移后符号位均不变，但若右移时最低数位丢1，可导致
√A. 影响运算精度
B. 无正确答案
C. 运算结果出错
D. 无任何影响

多选

13　若采用双符号位补码运算，运算结果的符号位为10，下列结论中错误的是
√A. 产生了上溢
B. 产生了下溢
C. 运算结果溢出，结果为负数
√D. 运算结果溢出，结果为正数

14　以下关于ALU的描述中，不正确的是
A. 支持算术与逻辑运算
√B. 只做逻辑运算
√C. 只做算术运算
√D. 只做加法与减法运算

15　假定有4个整数用8位补码分别表示r1=FEH，r2=F2H，r3=90H，r4=F8H，若将运算结果存放在一个8位的寄存器中，则下列运算不会发生溢出的是
√A. r2×r4
√B. r1×r4
C. r2×r3
√D. r1×r2

16　在浮点数加减法运算“规格化”步骤中，以下哪些尾数(假定采用补码表示)需要进行”左规”运算？（以下各数均为2进制表示）
A. 10.0100
B. 00.1000
√C. 00.0111
√D. 11.1000

17　以下说法正确的是
√A. n位小数的补码一位乘法（Booth算法），需做n+1次运算，第n+1次不移位
√B. 补码加减交替法是一种不恢复余数法
√C. 浮点运算可由阶码运算和尾数运算两个部分联合实现
√D. 在定点小数补码一位除法中，为了避免溢出，被除数的绝对值一定要小于除数的绝对值

18　以下关于算术移位和逻辑移位的描述正确的是
√A. 逻辑左移时，高位丢失，低位补0
√B. 算术左移时，相当于对原数乘2
√C. 算术右移时，符号位不变并向最高数据位复制
D. 逻辑右移时，相当于对原数除2

判断

19　运算器都会设置状态寄存器的目的是为实现程序转移提供判断条件
√A. 对
B. 错

20　为提高运算速度，运算器一般采用并行进位
A. 错
√B. 对

21　在浮点运算器，尾数运算部件只需要完成乘、除运算
A. 对
√B. 错

填空

22　已知[X]补 = 1101001 , [Y]补 = 1101010, 则用变形补码计算2[X]补 +1/2 [Y]补的结果为 （11000111）（直接填二进制数即可，数字间不留空格）

23　计算机字长为8位，若 x = - 1101101，则 [x/4]补 的值为 （11100100）（直接填写二进制数）

24　移码表示法主要用于表示浮点数的 （阶码） （直接填汉字即可）