java实现第二届蓝桥杯连通问题（C++）

连通问题、

BMP是常见的图像存储格式。

如果用来存黑白图像（颜色深度=1），则其信息比较容易读取。

与之相关的数据：

（以下偏移均是从文件头开始）

偏移：10字节, 长度4字节： 图像数据真正开始的位置。

偏移：18字节, 长度4字节： 位图的宽度，单位是像素。

偏移：22字节, 长度4字节： 位图的高度，单位是像素。

从图像数据开始处，每个像素用1个二进制位表示。

从图片的底行开始，一行一行向上存储。

Windows规定图像文件中一个扫描行所占的字节数必须是4字节的倍数，

不足的位均以 0 填充。例如，图片宽度为45像素，实际上每行会占用

8个字节。

可以通过Windows自带的画图工具生成和编辑二进制图像。

需要在“属性”中选择“黑白”，指定为二值图像。

可能需要通过 查看 | 缩放 | 自定义… 把图像变大比例一些，

更易于操作。

图像的左下角为图像数据的开始位置。白色对应1，黑色对应0

我们可以定义：两个点距离如果小于2个像素，则认为这两个点连通。

也就是说：以一个点为中心的九宫格中，围绕它的8个点与它都是连通的。

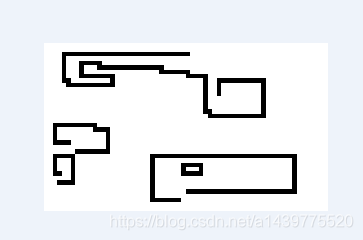
如：t1.bmp 所示，左下角的点组成一个连通的群体；

而右上角的点都是孤立的。

        in.bmp                                t1.bmp

程序的目标是：根据给定的黑白位图，分析出所有独立连通的群体，

输出每个连通群体的面积。所谓面积，就是它含有的像素的个数。

输入数据固定存在in.bmp中。

如示例的in.bmp,

程序应该输出：

81

133

该输出表示：共有4个连通群体。

输出的连通体面积间的顺序可以随意。

请编程解决上述问题。

我们测试程序的时候，会使用不同的in.bmp文件。

要求考生把所有类写在一个文件中。

调试好后，存入与考生文件夹下对应题号的“解答.txt”中即可。

相关的工程文件不要拷入。请不要使用package语句。

这题要读入图片文件数据，感觉头大啊，此前做的题，几乎没有遇到要读取文件中的数据，而现在竟然还碰到了读取图片的数据，看到此题的核心：即使用DFS求取连通图的问题，并且返回每一个连通图中包含的顶点个数，但是对于此题处理读取数据的问题，就没有仔细去探究，下面贴出一段网友的C语言代码，以作参考：

include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#include<string.h> 

void main(){
int i,j,k,m;
int width,height,start,world;
int *bmp,*Lcount;
bool *Lflag;
FILE *fp;
if((fp=fopen("in1.bmp","rb"))==NULL){
printf("文件打开失败");
return;
}
fseek(fp,10L,0);
fscanf(fp,"%4c",&start); // 4c表示该数据占4个字节
// printf("start = %d\n",start);
fseek(fp,18,0);
fscanf(fp,"%4c",&width);
// printf("width = %d\n",width);
fseek(fp,22,0);
fscanf(fp,"%4c",&height);
// printf("height = %d\n",height);
bmp = (int*)malloc((width+2)*sizeof(int));
memset(bmp,0,(width+2)*sizeof(int));
Lcount = (int*)malloc(width*sizeof(int));
memset(Lcount,0,width*sizeof(int));
Lflag = (bool*)malloc(width*sizeof(bool));
memset(Lflag,0,width*sizeof(bool));
Lcount--;
Lflag--;
fseek(fp,start,0);
world = ( width%32 ? width/32+1 : width/32 )*4;
int last,i1,i2,i3;
int eCount = 0
for(i=0 i<height i++ ){
char c;
k=1;
last=0;
for(j=0 j<world j++){
fscanf(fp,"%c",&c);
for(m = 7 m >= 0 && k<=width m-- ){
if( !( 1<<m & c ) ){
//printf("*");
if(bmp[k]){
last = bmp[k];
Lcount[last]++;
Lflag[last] = true
}
else{
i1 = last ? last : bmp[k-1]
i3 = bmp[k+1]
last = 0;
if( i1 || i3){
if( i1 && i3 && ( i1 != i3 ) ){//确定需要连接
Lcount[i1] += Lcount[i3]
Lcount[i3]=0;
for(i2=1;i2<=width i2++){
if(bmp[i2]==i3)
bmp[i2] = i1;
}
}
else{
if(!i1)
i1=i3;
}
bmp[k] = i1
Lcount[i1]++;
Lflag[i1] = true
}
else{//插入
for(i2=1;Lcount[i2];i2++);
Lcount[i2]=1;
bmp[k] = i2
Lflag[i2] = true
}
}
}
else{ //printf(" ");
last = bmp[k]
bmp[k] = 0
}
k++;
}
}
//printf("\n");
for(i2=1;i2<=width;i2++){
if(Lcount[i2] && !Lflag[i2] ){
printf("%d\n",Lcount[i2]);
Lcount[i2] = 0
eCount++;
}
Lflag[i2]=false;
}
}
fclose(fp);
free(Lflag+1);
free(Lcount+1);
free(bmp);
printf("count=%d\n",eCount);
}