xdoj-1243 (费马平方和问题）

1243: CKJ老师爱数学

时间限制: 1 Sec 内存限制: 128 MB
提交: 56 解决: 13
[提交][状态][讨论版]

题目描述

众所周知，CKJ老师非常热爱数学，他对于方程组的有自己的独到的研究，today，他抛给了你一个too simple的方程组x^2+y^2=z^2，z是一个已给的正整数，然后他毫不客气地问你，这个方程组的整数解有几个？

输入

包含一个整数T表示输入数据组数，

接下来T行每行一个整数z（z<=2000 000 000）

输出

每行一个整数表示方程组的解的个数

样例输入

1

4

样例输出

4
---------------------------------------------------------------------------------------------

自认为这是xdoj上思考最多的一道题：网上好像有这样题的公式，但做题最要的不是理解学习心得知识吗。

首先我贴出一些知识点：

1）定理 1 x² + y² = z² 的互質整數解為 x=2uv, y=u²-v², 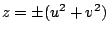，其中 u, v 是任意互質整數，且 u, v 不同時為奇數。

證明 1 令 x, y, z 是互質正整數，且 x² + y² = z²。若 x 與 y 都是奇數，則 z 是偶數。故 x² + y² 是 4l+2 的型式，z² 是 4l' 的型式（l 與 l' 是整數）。矛盾。

因此，不妨假定 x 是偶數，y 與 z 是奇數。

由 x² = z² - y² = (z+y) (z-y)，令 x=2r, z-y = 2s, z+y = 2t。得 r² = st。

s 與 t 互質，因 y 與 z 互質。但 st 是完全平方。故 s=u² , t=v²。得證。

网址链接：http://episte.math.ntu.edu.tw/articles/mm/mm_07_4_01/page3.html

2）定理二：费马平方和定理奇质数能表示为两个平方数之和的充分必要条件是该素数被4除余1。

3）定理三： (a^2+b^2)*(c^2+d^2)==(ac+bd)^2+(ad-bc)^2

网址链接: https://zh.wikipedia.org/wiki/%E8%B4%B9%E9%A9%AC%E5%B9%B3%E6%96%B9%E5%92%8C%E5%AE%9A%E7%90%86

问题解决：

1 借助定理1 将x^2+y^2=z^2 转化为 x^2+y^2=n 有多少整数解

2 每个整数解我们可以看出是由本原解组成（三个数互质）【 3，4，5】是，而【6，8，10】不是

3 z=p1^k1*p2^k2*....pn^kn

根据定理二对于每个素数pk且满足pk%4==1 一个本原解 a^2+b^2==pk

对于每一个素数要么可以充当本原解的组成，要么组成解的因子

所以对于每一个因子可以有（2*sum+1) 种选择

eg (z==25 sum=2 有五种选择

1+4=5; 解得x=5^2*(2*u*v)=4*25=100; y=25*(u^2-v*2)=75;【一个5是因子，一个5组成本原解】

3^2+4^2=25 解得y=2uv=24; x=u*2-v*2=7; 【两个5都是本原解】

两个解调换位置 4个解

25全部作为因子 1个解

）

4 根据定理三两个本原解可以合并乘一个本原解所以不同因子之间是相乘关系

一共有 ans=∏ (2*pk+1)-1 本原解【减一是排除所有素数作为因子】

考虑正负号 ans*=4

再加上四个点 sum=ans+4; 【端点我们不认为是本原解】

 #include<cstdio>

 #include<algorithm>

 #include<iostream>

 using namespace std;

 typedef long long LL;

 const LL N=1e6+;

 LL p[N+];

 int main ()

 {

     for (LL i=;i<=N;i++) {

         if (!p[i]) p[++p[]]=i;

         for (LL j=;j<=p[]&&i*p[j]<=N;j++) {

             p[i*p[j]]=;

             if (i%p[j]==)  break;

         }

     }

     int T;

     scanf ("%d",&T);

     while (T--) {

         LL x;

         scanf("%lld",&x);

         LL i=;

         LL ans=;

         while (p[i]*p[i]<=x) {

             LL sum=;

             if (x%p[i]==) {

                 while (x%p[i]==) {

                     sum++;

                     x=x/p[i];

                 }

                 if (p[i]%==)

                     ans=ans*(*sum+);

             }

             i++;

         }

         if(x!=&&(x%==)) ans=ans*;

         printf("%lld\n",(ans-)*+);

     }

     return ;

 }

这完全是我自己的理解，可能存在说的不清晰地方或者不严谨，请

多多指教；