D-Big Integer_2019牛客暑期多校训练营（第三场）

题意

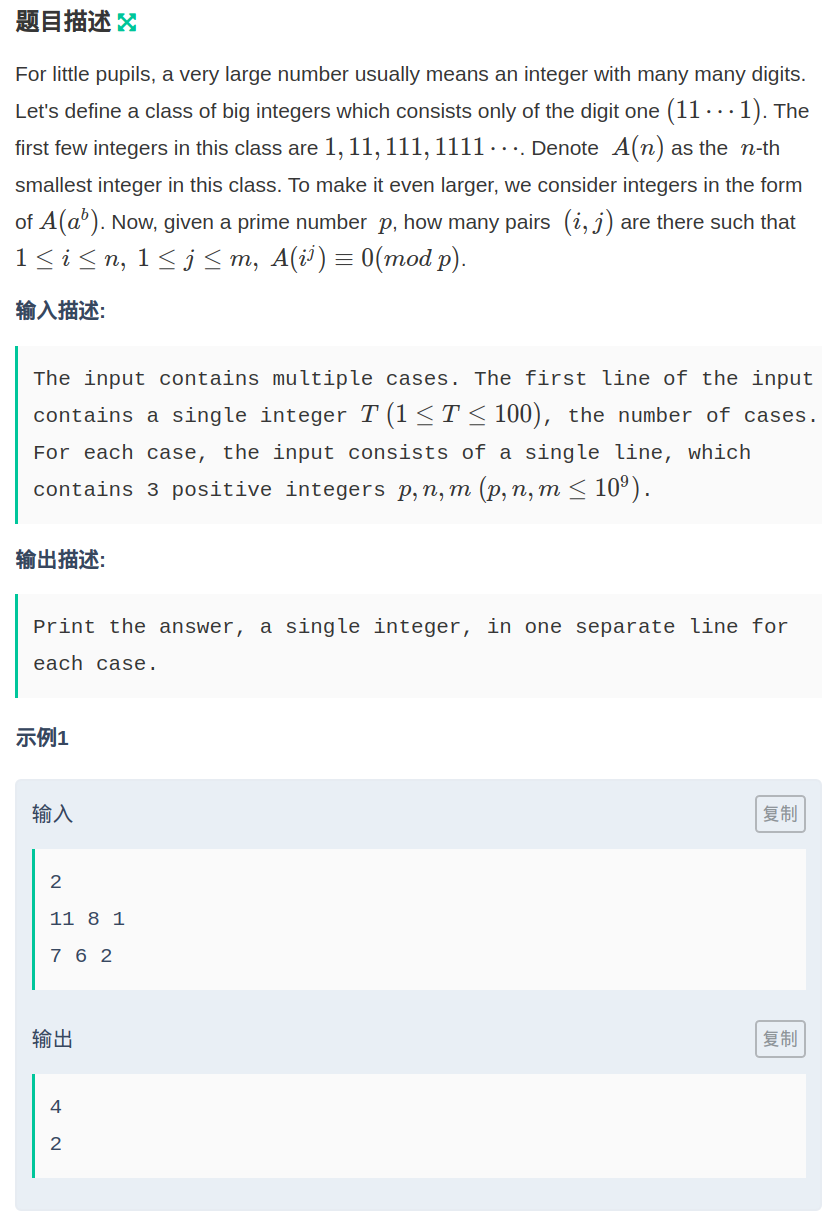
设A(n) = n个1,问有多少对i,j使得\(A(i^j)\equiv0(modp)\)

题解

\(A(n) = \frac{10^n-1}{9}\)

当9与p互质时\(\frac{10^n-1}{9}\%p = (10^n-1)\cdot inv[9] \% p\)

移动项得到\(10^n\equiv1(modp)\)

由欧拉定理当\(gcd(10,p) = 1\)时\(10^{\varphi(p)}\equiv1(modp)\)

那么只要找到最小的d使得\(10^d\equiv1(modp)\)

问题就转化成求有多少对i,j使得\(i^j\equiv0(modp)\)

求d只需要枚举\(\varphi(p)\)的因子就好了

对d分解\(d = p_1^{k_1}p_2^{k_2}\cdots p_n^{k_n}\)

固定j，要使\(i^j\)是d的倍数，那么i一定是\(p_1^{\lceil\frac{k_1}{j}\rceil}p_2^{\lceil\frac{k_2}{j}\rceil}\cdots p_n^{\lceil\frac{k_n}{j}\rceil}\)的倍数

设\(g_j = p_1^{\lceil\frac{k_1}{j}\rceil}p_2^{\lceil\frac{k_2}{j}\rceil}\cdots p_n^{\lceil\frac{k_n}{j}\rceil}\),答案就是\(\sum_{j=1}^mg_j\),因为\(k_i\)不会超过30，

当j大于30时的\(g_j\)都一样就不用重复计算了

还有一个问题，当p=3时，因为9与3不互质,inv[9]不存在，式子\(\frac{10^n-1}{9}\%p \Longleftrightarrow (10^n-1)\cdot inv[9] \% p\)

就不成立，需要特判，此时d取3

代码

#include <bits/stdc++.h>

using namespace std;
const int mx = 3e5+10;
typedef long long ll;

ll pow_mod(ll a, ll b, ll mod) {
    ll ans = 1;
    while (b > 0) {
        if (b & 1) ans = ans * a % mod;
        a = a * a % mod;
        b /= 2;
    }
    return ans;
}

ll pow_mod(ll a, ll b) {
    ll ans = 1;
    while (b > 0) {
        if (b & 1) ans = ans * a;
        a = a * a;
        b /= 2;
    }
    return ans;
}

vector <ll> pp, k;

int main() {
    int T;
    scanf("%d", &T);

    while (T--) {
        ll p, n, m, d;
        scanf("%lld%lld%lld", &p, &n, &m);
        if (p == 2 || p == 5) {
            printf("0\n");
            continue;
        }
        d = p-1;
        for (ll i = 1; i*i <= (p-1); i++) {
            if ((p-1) % i == 0) {
                if (pow_mod(10, i, p) == 1) {
                    d = min(d, i);
                }
                if (pow_mod(10, (p-1)/i, p) == 1) {
                    d = min(d, (p-1)/i);
                }
            }
        }
        if (p == 3) d = 3;
        pp.clear(); k.clear();
        ll ans = 0;
        for (ll i = 2; i*i <= d; i++) {
            if (d % i == 0) {
                int tmp = 0;
                while (d % i == 0) {
                    tmp++;
                    d /= i;
                }
                k.push_back(tmp);
                pp.push_back(i);
            }
        }
        if (d > 1) pp.push_back(d), k.push_back(1);

        ll tmp = 1;
        for (int i = 1; i <= min(30LL, m); i++) {
            tmp = 1;
            for (int j = 0; j < pp.size(); j++) {
                ll b = k[j] / i;
                if (k[j] % i != 0) b++;
                tmp *= pow_mod(pp[j], b);
            }
            ans += n / tmp;
        }
        if (m > 30) ans += n / tmp * (m-30);
        printf("%lld\n", ans);
    }
    return 0;
}