NOIP模拟 13

　　我终于又厚颜无耻地赖着没走

　　......

　　T1 矩阵游戏

　　　　用了30hmin找规律，然后发现貌似具有交换律，然后发现貌似有通项公式，然后发现貌似每次操作对通项的影响是相同的，然后发现貌似跟N没啥关系...

　　　　确认过复杂度，是遇上了正解。

　　　　开心啊，码了1h，到八点半还过不去样例（skyh早做完了好像还过对拍了好像还高兴够呛），我都想弃了

　　　　突然过样例，看了看时间，只能放弃了给T1打对拍的习惯...

　　　　结束前半小时心态爆炸的时候给它补上了对拍放松心情233

　　T2 跳房子

　　　　考场上只打了NK模拟，虽然想出了循环节但是已经没信心去打了

　　　　传说中的分块思想被我打炸了，虽然后来颓到了贪心正确性的证明

　　　　但是还是用%%orz tkj线段树维护映射的做法做掉了

　　　　讲真那种做法真的挺优美的..

　　

　　T3 优美序列

　　　　奇袭就不提了，当初颓的一批哪里还记得分治

　　　　于是新颓了一个题解..%%orz starsing

　　　　首先设一段区间内值域相邻的对数为num，则当l+num==r时，这是个优美区间

　　　　维护一个单调指针从左往右滑，每滑到一个新点，检查对num是否有贡献

　　　　然后用线段数维护r之前的点l到r这个区间的num（神奇，不知道怎么能想到）

　　　　其实为了方便，维护的是l+num，查询时直接与r比较，修改就是区间加

　　　　

　　　　那么每移动一次r，可以知道可以更新哪些l了，可是还不知道应该何时更新

　　　　找到第一个可更新此区间的r时，就用小于待询区间l的最大l更新（其实只是赋值一次）待询区间的答案即可。

　　　　1.首先这个r是最小的r没问题吧，因为这是你第一次扫到

　　　　2.那你可能说了，将来会不会有更大的l出现，使得即使r也增大但是答案更优

　　　　3.偷starsing一张图：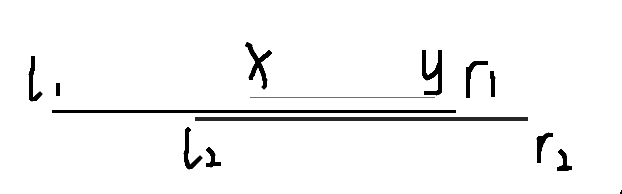

　　　　　r1是你刚刚扫到的r，l1是刚刚用线段树找到的l，r2是你期望的r，l2是期望更大的l

　　　　　所以[l1,r1]，[l2,r2]都是优美区间...

　　　　　妙的是，[l2,r1]也一定是优美区间。

　　　　　不然呢，如果它不连续，那么它缺失的值域一定在左（右）边，右（左）边的区间就不可能优美了.

　　　　4.所以未来更优只是没经过分析yy出来的，还是尽快抓住现在取到最优解吧