CF1028C Rectangles 思维

 Rectangles

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given nn rectangles on a plane with coordinates of their bottom left and upper right points. Some (n−1)(n−1) of the given nnrectangles have some common point. A point belongs to a rectangle if this point is strictly inside the rectangle or belongs to its boundary.

Find any point with integer coordinates that belongs to at least (n−1)(n−1) given rectangles.

Input

The first line contains a single integer nn (2≤n≤1326742≤n≤132674) — the number of given rectangles.

Each the next nn lines contains four integers x1x1, y1y1, x2x2 and y2y2 (−109≤x1<x2≤109−109≤x1<x2≤109, −109≤y1<y2≤109−109≤y1<y2≤109) — the coordinates of the bottom left and upper right corners of a rectangle.

Output

Print two integers xx and yy — the coordinates of any point that belongs to at least (n−1)(n−1) given rectangles.

Examples

input

Copy

3
0 0 1 1
1 1 2 2
3 0 4 1

output

Copy

1 1

input

Copy

3
0 0 1 1
0 1 1 2
1 0 2 1

output

Copy

1 1

input

Copy

4
0 0 5 5
0 0 4 4
1 1 4 4
1 1 4 4

output

Copy

1 1

input

Copy

5
0 0 10 8
1 2 6 7
2 3 5 6
3 4 4 5
8 1 9 2

output

Copy

3 4

Note

The picture below shows the rectangles in the first and second samples. The possible answers are highlighted.

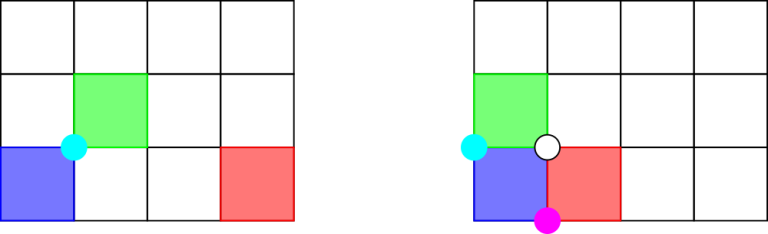
The picture below shows the rectangles in the third and fourth samples.

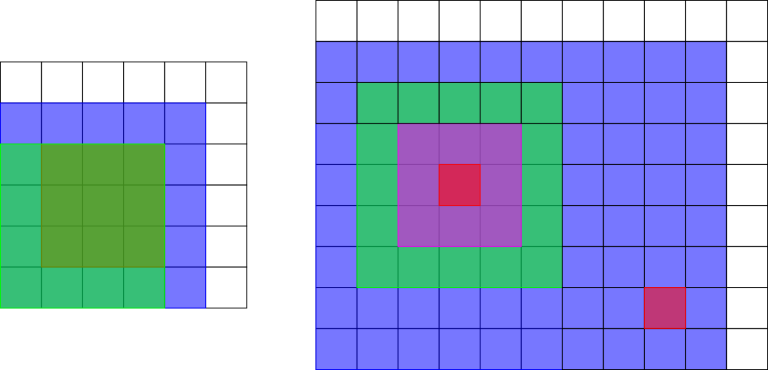
题意：输出任意一个处于至少n-1个矩形相交区域的点

分析：考虑对于第i个矩形，如果不包括他，前面的i-1个矩形和后面的n-i个矩形是否可以有相交区域，如果有就一定有点处于其中，这个点也就位于n-1个矩形相交区域

　　　我们可以在开始的时候求出前面i个矩形的相交区域pre[i]和后面i个矩形的相交区域pos[i]，然后再遍历一次循环求当前矩形前面的矩形和后面矩形的相交区域pre[i-1]相交pos[i+1]

AC代码：

#include <map>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <string>
#include <bitset>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#define ls (r<<1)
#define rs (r<<1|1)
#define debug(a) cout << #a << " " << a << endl
using namespace std;
typedef long long ll;
const ll maxn = 232674;
const double eps = 1e-8;
const ll mod = 1e9 + 7;
const ll inf = 1e9;
const double pi = acos(-1.0);
struct node {
    ll x1, y1, x2, y2;
};
node a[maxn], pre[maxn], pos[maxn];
int main() {
    ll n;
    cin >> n;
    for( ll i = 1; i <= n; i ++ ) {
        cin >> a[i].x1 >> a[i].y1 >> a[i].x2 >> a[i].y2;
    }
    node st = a[1], ed = a[n];
    pre[0].x1 = -2e9, pre[0].y1 = -2e9, pre[0].x2 = 2e9, pre[0].y2 = 2e9;
    pos[n+1].x1 = -2e9, pos[n+1].y1 = -2e9, pos[n+1].x2 = 2e9, pos[n+1].y2 = 2e9;
    for( ll i = 1, j = n; i <= n; i ++, j -- ) {
         st.x1 = max(st.x1,a[i].x1), st.y1 = max(st.y1,a[i].y1);
         st.x2 = min(st.x2,a[i].x2), st.y2 = min(st.y2,a[i].y2);
         pre[i] = st;
         ed.x1 = max(ed.x1,a[j].x1), ed.y1 = max(ed.y1,a[j].y1);
         ed.x2 = min(ed.x2,a[j].x2), ed.y2 = min(ed.y2,a[j].y2);
         pos[j] = ed;
    }
    for( ll i = 1; i <= n; i ++ ) {
        node t;
        t.x1 = max(pre[i-1].x1,pos[i+1].x1), t.y1 = max(pre[i-1].y1,pos[i+1].y1);
        t.x2 = min(pre[i-1].x2,pos[i+1].x2), t.y2 = min(pre[i-1].y2,pos[i+1].y2);
        if( t.x2-t.x1 >= 0 && t.y2-t.y1 >= 0 ) {
            cout << t.x1 << " " << t.y1 << endl;
            break;
        }
    }
    return 0;
}