ZOJ 3537 Cake (凸包 + 区间DP && 最优三角形剖分)

题目链接：Here

题意：

给定 \(n\)​​ 个点的坐标，先问这些点能否组成一个凸包，如是凸包，问用不相交的线来切这个凸包使得凸包只由三角形组成，根据 \(cost_{i, j} = |x_i + x_j| * |y_i + y_j| \% p\)​​​​算切线的费用，问最少的切割费用。

解题思路：参考于 ZeroClock，感谢！

经典的最优三角剖分模型加一点计算几何的知识。

先判断是否为凸包，这个排个序就好弄，搬了一下凸包函数排序的板子。

返回凸包中的顶点数量再与 \(n\) 比较。

这一步处理完之后就是用 \(n-3\) 条直线将凸包切成 \(n-2\) 个三角形。

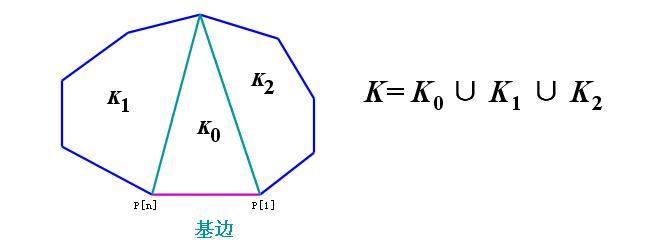
我们要切的是以 \(1\) 和 \(n\) 为起始点的凸包，由于切线不能相交，那么选择 \(1\) 点和 \(n\) 点必有另外一点 \(S\) 要和它们组成一个三角形，然后凸包被分成三个部分: \(k_0,k_1,k_2\) ，然后把 \(k_1\) 看成一个以 \(n\) 点 \(S\) 点位起始点的凸包，是不是又可以用相同的方法处理这个凸包呢？答案是肯定，就是这样慢慢地将凸包分成一个个子凸包计算费用，最后再更新到点 \(1\) 和点 \(n\) 为起始点的凸包。

模拟上面的过程，设 \(Dp[i][j]\)​​ 为以 \(i\)​ 为起点，\(j\)​ 为终点的凸包被切割成一个个小三角形所需要的费用。

那么 ​

\[dp[i][j] = min(dp[i][k]+dp[k][j]+cost[i][k]+cost[k][j]),(j >= i+ 3,i+1<=k<=j-1,cost[i][k]
\]

为连一条 \(i\) 到 \(k\) 的线的费用)，因为 \(dp[i][j]\) 只表示为以 \(i\) 为起点，\(j\) 为终点的凸包内部被切割的费用，所以在连线的时候可以加上边界费用而不算重复计算。

const int N = 1e3 + 10, inf = 1e9;
struct Point {
    int x, y;
} p[N];
int cost[N][N], n, m;
int f[N][N];

int abs(int x) {return x < 0 ? -x : x;}
int xmul(Point p1, Point p2, Point p0) {
    return (p1.x - p0.x) * (p2.y - p0.y) - (p2.x - p0.x) * (p1.y - p0.y);
}
bool cmp(const Point &a, const Point &b) {
    if (a.y == b.y)return a.x < b.x;
    return a.y < b.y;
}

Point save[400], temp[400];
int Graham(Point *p, int n) {
    sort(p, p + n, cmp);
    save[0] = p[0];
    save[1] = p[1];
    int top = 1;
    for (int i = 0; i < n; ++i) {
        while (top && xmul(save[top], p[i], save[top - 1]) >= 0) top --;
        save[++top] = p[i];
    }
    int mid = top;
    for (int i = n - 2; i >= 0; --i) {
        while (top > mid && xmul(save[top], p[i], save[top - 1]) >= 0) top --;
        save[++top] = p[i];
    }
    return top;
}
int Count(Point a, Point b) {
    return (abs(a.x + b.x) * abs(a.y + b.y)) % m;
}
int main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    while (cin >> n >> m) {
        for (int i = 0; i < n; ++i) cin >> p[i].x >> p[i].y;
        int tot = Graham(p, n); // 求凸包
        if (tot < n) {cout << "I can't cut.\n"; continue;}

        memset(cost, 0, sizeof(cost));
        // for (int i = 0; i < N; ++i) for (int j = 0; j < N; ++j)cost[i][j] = 0;
        for (int i = 0; i < n; ++i)
            for (int j = i + 2; j < n; ++j) cost[j][i] = cost[i][j] = Count(save[i], save[j]);

        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) f[i][j] = inf;
            f[i][(i + 1) % n] = 0;
        }
        for (int i = n - 3; i >= 0; --i) // 注意三个for循环顺序
            for (int j = i + 2; j < n; ++j) //因为要保证在算dp[i][j]时dp[i][k]和dp[k][j]时已经计算，所以i为逆序，j要升序
                for (int k = i + 1; k <= j - 1; ++k)
                    f[i][j] = min(f[i][j], f[i][k] + f[k][j] + cost[i][k] + cost[k][j]);

        cout << f[0][n - 1] << "\n";
    }
}