Solution Set -「NOI Online R1」

NOI-Online-T1-序列

其实这道题是全场最难的……

我这里给出一种并查集的做法。

首先我们把操作2中的 \(u\) 和 \(v\) 合并

对于操作1我们可以把他转化为操作2来做。

比如我们针对操作1给出 \((u,v)\) 和 \((v,t)\) 两条边，对 \((u,v)\) 进行同增，对 \((v,t)\) 进行同减。

这样就变成了 \(u++,t--\) 了。

然后我们把操作2缩点，然后把操作1的边连到操作2缩的点上。

然后对操作1合并。

此时，图中的每个点的度数最多为一。

那么对于一条边 \((x,y)\) 如果 \(a_{x}-b_{x}=a_{y}-b_{y}\) 那么就是YES；

对于一个自环 \((x,x)\) 如果 \((a_{x}-b_{x})\) 为偶数，那么就是YES；

对于一个度数为零的点 \(x\) 如果 \(a_{x}=b_{x}\) 那么就是YES；

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>

using namespace std;

char buf[1 << 21], *p1 = buf, *p2 = buf;
#ifndef ONLINE_JUDGE
#define gc() getchar()
#else
#define gc() (p2 == p1 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
#endif
#define is_number (ch >= '0' && ch <= '9')

template < typename Type >
void read(Type& a) {
    a = 0; bool f = 0; char ch;
    while (!(ch = gc(), is_number)) if (ch == '-') f = 1;
    while (is_number) a = (a << 3) + (a << 1) + (ch ^ '0'), ch = gc();
    a = (f ? -a : a);
}

template < typename Type, typename... Args >
void read(Type& t, Args&... args) {
    read(t), read(args...);
}

const int MAXN = 2e5 + 5;
int T, n, m, vis[MAXN];
int u[MAXN], v[MAXN];
int a[MAXN], b[MAXN];
int nxt[MAXN], to[MAXN];
int head[MAXN], tot;
struct UnionFindSet {
	int fa[MAXN];

	void init(int n) {
		for (int i = 1; i <= n; ++i)
			fa[i] = i;
	}

	int find(int x) {
		if (x ^ fa[x]) fa[x] = find(fa[x]);
		return fa[x];
	}

	void merge(int x, int y) {
		int u = find(x);
		int v = find(y);
		if (u ^ v) {
			fa[v] = u;
			a[u] += a[v];
			b[u] += b[v];
		}
	}
} ufs;

void add(int x, int y) {
	to[++tot] = y;
	nxt[tot] = head[x];
	head[x] = tot;
}

signed main() {
	for (read(T); T; --T) {
        read(n, m);
		tot = 0;
		memset(head, 0, sizeof head);
		ufs.init(n);
		for (int i = 1; i <= n; ++i) read(a[i]);
		for (int i = 1; i <= n; ++i) read(b[i]);
		for (int i = 1, opt; i <= m; ++i) {
		    read(opt, u[i], v[i]);
			if (opt ^ 1) vis[i] = 1, ufs.merge(u[i], v[i]), --i, --m;
		}
		for (int i = 1; i <= m; ++i) {
			add(ufs.find(u[i]), ufs.find(v[i]));
			add(ufs.find(v[i]), ufs.find(u[i]));
		}
		for (int i = 1; i <= n; ++i) {
			int t = ufs.find(to[head[i]]);
			for (int x = nxt[head[i]]; x; x = nxt[x])
				ufs.merge(t, ufs.find(to[x]));
		}
		for (int i = 1; i <= n; ++i) {
			if (head[i]) {
				int x = ufs.find(i);
				int y = ufs.find(to[head[i]]);
				if (x ^ y) {
					if ((a[x] - b[x]) ^ (a[y] - b[y])) {
						puts("NO");
						goto there;
					}
				}
				else {
					if ((a[x] - b[y]) & 1) {
						puts("NO");
						goto there;
					}
				}
			}
			else if (ufs.fa[i] == i) {
				if (a[i] ^ b[i]) {
					puts("NO");
					goto there;
				}
			}
		}
		puts("YES");
		there: ;
	}
}

NOI-Online-T2-冒泡排序

这道题我在考场上的做法很玄，本来是奔着40pts的部分分去的，结果爆零了(至今没找到原因)

我们设

\[bigger_{i}=\sum_{j=1}^{i-1}[a_{j}>a_{i}]
\]

显然逆序对数量为 \(\sum bigger\)

于是问题就转化为了动态维护 \(bigger\)。

手玩几组数据后我们可以发现，每轮冒泡 \(bigger\) 都会有一下的变化：

\[bigger_{i}=\max\{bigger_{i}-1,0\}
\]

于是树状数组维护即可

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>

char buf[1 << 21], *p1 = buf, *p2 = buf;
#ifndef ONLINE_JUDGE
#define gc() getchar()
#else
#define gc() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
#endif
#define is() (ch >= '0' && ch <= '9')
template < typename Type >
void read(Type& a) {
	a = 0; bool f = 0; char ch;
	while (!(ch = gc(), is())) if (ch == '-') f = 1;
	while (is()) a = (a << 3) + (a << 1) + (ch ^ '0'), ch = gc();
	a = (f ? -a : a);
}

template < typename Type, typename... Args >
void read(Type& t, Args&... args) {
	read(t), read(args...);
}

using namespace std;

const int MAXN = 2e5 + 5;
int n, m, bigger[MAXN], bucket[MAXN], a[MAXN];
long long bit[MAXN], init_inver_tot;

void Update(int x, long long y) {
	for (; x <= n; x += x & -x) bit[x] += y;
}

long long GetAnswers(int x) {
	long long res = 0;
	for (; x; x -= x & -x) res += bit[x];
	return res;
}

signed main() {
	read(n, m);
	for (int i = 1; i <= n; ++i) read(a[i]), init_inver_tot += (bigger[i] = i - 1 - GetAnswers(a[i])), bucket[bigger[i]]++, Update(a[i], 1);
	memset(bit, 0, sizeof bit), Update(1,  init_inver_tot), init_inver_tot = 0;
	for (int i = 0; i < n; ++i) init_inver_tot += 1LL * bucket[i], Update(i + 1 + 1, init_inver_tot - n);
	for (int i = 0, op, x; i < m; ++i) {
		read(op, x);
		if (n - 1 < x) x = n - 1;
		if (op ^ 2) {
			if (a[x + 1] > a[x]) {
				swap(a[x], a[x + 1]);
				swap(bigger[x], bigger[x + 1]);
				Update(1, 1);
				Update(bigger[x + 1]++ + 2, -1);
			}
			else {
				swap(a[x], a[x + 1]);
				swap(bigger[x], bigger[x + 1]);
				Update(1, -1);
				Update(--bigger[x] + 2, 1);
			}
		}
		else printf("%lld\n", GetAnswers(x + 1));
	}
	return 0;
}

NOI-Online-T3-最小环

全场最水的一道题，但是可怕的心理作用还是让我放弃了这道题。

首先有一个显然的结论，我们需要把这 \(n\) 个数分为 \(\gcd(n,k)\) 个环。

虽说是显然但是不画画图还真的玩不动

给一下图示意一下：

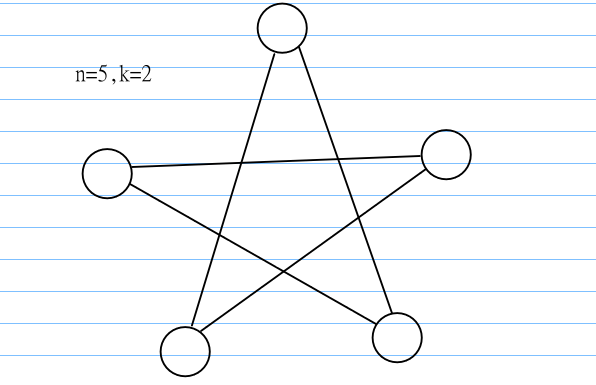
图中那个看起来像个五角星的东西其实就是个环

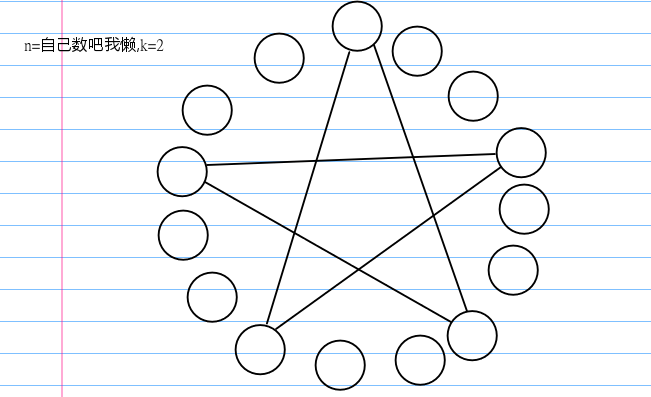
这个图中有 \(\gcd(n,k)\) 个环，这就是我们的结论。

具体到实现，我们采用的是预处理出所有答案。

还有 \(k=0\) 的情况需要特殊处理一下

#include <cstdio>
#include <algorithm>
#include <queue>

using namespace std;

const int MAXN = 5e5 + 5;
vector < int > integer(MAXN);
vector < long long > ans(MAXN);

int gcd(int x, int y) {
	return !y ? x : gcd(y, x % y);
}

signed main() {
	int n, k;
	scanf("%d %d", &n, &k);
	for (int i = 1; i <= n; ++i) scanf("%d", &integer.at(i)), ans.at(0) += (long long)integer.at(i) * (long long)integer.at(i);
	sort(integer.begin() + 1, integer.begin() + 1 + n);
	for (int i = 1; i <= (n >> 1); ++i) {
		if (!(n % i)) {
			int t = n / i;
			vector < int > process(MAXN);
			int tot = 0;
			for (int j = 2; j < t; j += 2) process.at(++tot) = j;
			process.at(++tot) = t;
			for (int j = t - 1 - (t & 1); j > 0; j -= 2) process.at(++tot) = j;
			for (int j = t + 1; j <= n; ++j) process.at(j) = process.at(j - t) + t;
			for (int j = 1; j <= n; ++j)
				if (!(j % t)) ans.at(i) += (long long)integer.at(process.at(j)) * (long long)integer.at(process.at(j + 1 - t));
				else ans.at(i) += (long long)integer.at(process.at(j)) * (long long)(integer.at(process.at(j + 1)));
		}
	}
	for (int i = 0, x; i < k; ++i) scanf("%d", &x), printf("%lld\n", ans.at(x ? gcd(n, x) : 0));
	return 0;
}

总结

（其实我不是很会写这玩意儿）

果然心理素质还是不行……错过了T3这样的水题。

总体来说，把握住机会，把题目都当作大白菜（雾）。

然后就是多去做题吧，题量多少都不嫌多。

就这样（

普及组口胡

说了是口胡所以没代码不保证正确/xyx

至于题目难度这是NOIOL不是NOIpOL给了搬出题人放飞自我的空间。

T1：普通NOIp普及难度，各位巨佬随便切

T2: 基础多项式，会的人就很套路。不会的话就n方dp骗骗分

T3: 这道题我不太确定，应该是Floyd+矩阵。

完结撒六花