Codeforces[CF1036B]Diagonal Walking v.2题解

题目大意

很明显，这道题就是求 k 步之内到达点 \((a,b)\) ，然后尽量走对角线，求能走对角线的最大值。

做题思路

首先明白一个事实，即一个对角线可以通过增加一步而抵达点不变，如图：

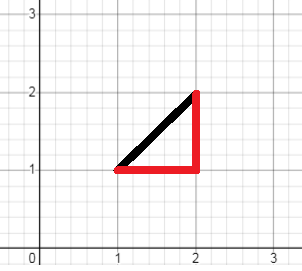
我们可以这样思考这道题，在到达目的地以后，剩余步数如果为双数，则在对角线来回走，最后会到目的地。但如果剩余步数为单数，我们通过上图转化最后依旧到达目的地。

现在考虑什么时候输出-1，即为走完k步后仍无法到达目的地，考虑从原点到达目的地需要的最小步数即为 \(max(a,b)\)

所以排除掉无法到达的情况，我们分类讨论：

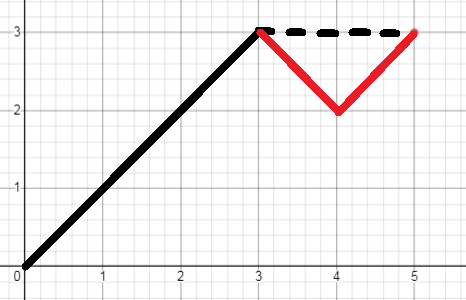
1. 设 a 和 b 中，a 为较大的一个数，如果 (a-b)%2==0 ,那么走对角线我们会先到达 b 的限定高度，考虑优化走到 a 的路线，以 \((5,3)\) 为例，走到3的限定高度后，如果剩余路线为双数，考虑上下跳走,答案 \(k\) 。：
   
   

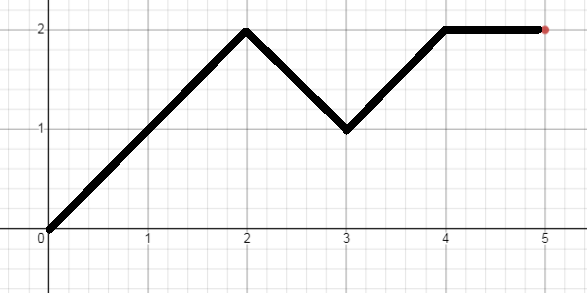
2. 依旧设 a 为较大的一数，如果(a-b)%2==1 ，那么我们只好消耗一格走平路以到达目的地，答案 \(k-1\) ，以 \((5,2)\) 为例：
   
   

最后，我们只需要判断一下剩余的步数能不能全部在对角线上反复横跳。如果不行，则贡献为-2（开头讲了）

线上AC代码：

#include<bits/stdc++.h>
using namespace std;
long long t,n,m,k;
int main(){
    scanf("%lld",&t);
    while(t--){
        scanf("%lld%lld%lld",&n,&m,&k);
        if(k<max(n,m)){
        	printf("-1\n");
        	continue;
        }
        if((max(n,m)-min(n,m))%2==1) k--;
        else if((k-max(n,m))%2==1) k-=2;
        printf("%lld\n",k);
    }
	return 0;
}

---

在此补充一个我有点迷糊的点，即为什么判断 if((max(n,m)-min(n,m))%2==1) 后，不用再次判断剩余的 k 是否为为双数，上图，

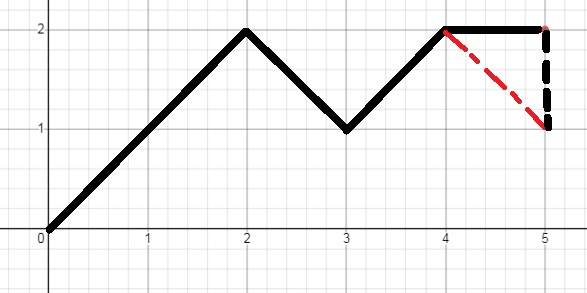
满足 if((max(n,m)-min(n,m))%2==1) 意味着我们到达目的地之前至少走了一个平路，此时若 k 为单数，直接将多的一个平路改为对角线加平路（还是最开始将的三角转换），如上图。