HTML5实战—canvas绘图之贝塞尔曲线
1、二次贝塞尔曲线
quadraticCurveTo(cpx,cpy,x,y) //cpx,cpy表示控制点的坐标, x,y表示终点坐标;
数学公式表示如下:
二次方贝兹曲线的路径由给定点P0、P1、P2的函数B(t)追踪:
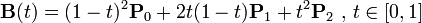

代码实例:

<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>canvas直线</title>
<meta name="Keywords" content="">
<meta name="author" content="@my_programmer">
<style type="text/css">
body, h1{margin:0;}
canvas{margin: 20px;}
</style>
</head>
<body onload="draw()">
<h1>二次贝塞尔曲线</h1>
<canvas id="canvas" width=200 height=200 style="border: 1px solid #ccc;"></canvas>
<script>
function draw() {
var canvas=document.getElementById('canvas');
var context=canvas.getContext('2d');
//绘制起始点、控制点、终点
context.beginPath();
context.moveTo(20,170);
context.lineTo(130,40);
context.lineTo(180,150);
context.stroke(); //绘制2次贝塞尔曲线
context.beginPath();
context.moveTo(20,170);
context.quadraticCurveTo(130,40,180,150);
context.strokeStyle = "red";
context.stroke();
}
</script>
</body>
</html>

代码效果:

2、三次贝塞尔曲线
bezierCurveTo(cp1x,cp1y,cp2x,cp2y,x,y) //cp1x,cp1y表示第一个控制点的坐标, cp2x,cp2y表示第二个控制点的坐标, x,y表示终点的坐标;
数学公式表示如下:
P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于P0走向P1,并从P2的方向来到P3。一般不会经过P1或P2;这两个点只是在那里提供方向资讯。P0和P1之间的间距,决定了曲线在转而趋进P3之前,走向P2方向的“长度有多长”。
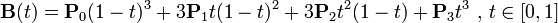

代码实例:

<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>canvas直线</title>
<meta name="Keywords" content="">
<meta name="Description" content="">
<style type="text/css">
body, h1{margin:0;}
canvas{margin: 20px; }
</style>
</head>
<body onload="draw()">
<h1>三次贝塞尔曲线</h1>
<canvas id="canvas" width=200 height=200 style="border: 1px solid #ccc;"></canvas>
<script>
function draw() {
var canvas=document.getElementById('canvas');
var context=canvas.getContext('2d');
//绘制起始点、控制点、终点
context.beginPath();
context.moveTo(25,175);
context.lineTo(60,80);
context.lineTo(150,30);
context.lineTo(170,150);
context.stroke(); //绘制3次贝塞尔曲线
context.beginPath();
context.moveTo(25,175);
context.bezierCurveTo(60,80,150,30,170,150);
context.strokeStyle = "red";
context.stroke();
}
</script>
</body>
</html>

代码效果图:

【出处】:https://www.cnblogs.com/duanhuajian/archive/2012/10/15/2725096.html
【声明】:所有博文标题后加(share)的表示收集的他人优秀文章,其余的则为原创。欢迎转载,但请在显要位置显示本文链接,并保留本段声明,否则追究法律责任,谢谢!
HTML5实战—canvas绘图之贝塞尔曲线的更多相关文章
- 用html5的canvas画布绘制贝塞尔曲线
查看效果:http://keleyi.com/keleyi/phtml/html5/7.htm 完整代码: <!DOCTYPE html PUBLIC "-//W3C//DTD XHT ...
- 基于canvas二次贝塞尔曲线绘制鲜花
canvas中二次贝塞尔曲线参数说明: cp1x:控制点1横坐标 cp1y:控制点1纵坐标 x: 结束点1横坐标 y:结束点1纵坐标 cp2x:控制点2横坐标 cp2y:控制点2纵坐标 z:结束点2横 ...
- Canvas中绘制贝塞尔曲线
① 什么是贝塞尔曲线? 在数学的数值分析领域中,贝济埃曲线(英语:Bézier curve,亦作“贝塞尔”)是计算机图形学中相当重要的参数曲线.更高维度的广泛化贝济埃曲线就称作贝济埃曲面,其中贝济埃三 ...
- HTML5之Canvas绘图——使用Canvas绘制图形的基本教程
原文转自:http://www.cnblogs.com/picaso/archive/2012/11/26/2789077.html HTML5火的正热,最近有个想法也是要用到HTML的相关功能,所以 ...
- HTML5之Canvas绘图(一) ——基础篇
HTML5火的正热,最近有个想法也是要用到HTML的相关功能,所以也要好好学习一把. 好好看了一下Canvas的功能,感觉HTML5在客户端交互的功能性越来越强了,今天看了一下Canvas绘图,下边是 ...
- 【HTML5】Canvas绘图详解-1
----->Canvas绘制基础 1,线条绘制 1-1,线条组成的图形和beginPath 案例:绘制由不同颜色的线条组成的图案 1-2,多边形的填充和closePath 案例:绘制封闭具有填充 ...
- HTML5之Canvas绘图实例——饼状图
实现饼状分布画图(如下):调试环境:Firefox
- HTML5之Canvas绘图实例——曲线图
实现正弦.余弦和正切函数画图(如下图):调试环境:Firefox
- HTML5七巧板canvas绘图(复习)
<!DOCTYPE html> <html xmlns="http://www.w3.org/1999/xhtml"> <head> <m ...
- HTML5七巧板canvas绘图
<!DOCTYPE html> <html xmlns="http://www.w3.org/1999/xhtml"> <head> <m ...
随机推荐
- 【工具】-Reverse-DIE(Detect-It-Easy)
关于 Detect It Easy,或缩写为"DIE"是一个用于确定文件类型的程序.Detect It Easy 是一个多功能的 PE 检测工具,基于 QT 平台编写,主要用于 P ...
- 解决使用sqlalchemy时MySQL密码含有特殊字符问题
前言 当MySQL密码中含有特殊字符时,使用sqlalchemy大概率连不上,这时候就需要from urllib.parse import quote_plus as urlquote. 示例代码 f ...
- jsp+servlet实战项目
第一步:新建maven项目,项目中添加dao,entity,service,servlet,util包第二步:导入依赖 第三步:数据库建表 第四步:entity实体包(疯转) 第五步:在util工具包 ...
- 让C#调用vue组件里的方法
前言:web页面开发时采用的是vue开发的,后台语言是C# 需求:后台需要通过浏览器调用vue组件的方法 c# 可以调用xxx.html 中的script引用的js中定义的方法是可以调用的, 之前c# ...
- 【腾讯云 Cloud Studio 实战训练营】在线 IDE 编写 canvas 转换黑白风格头像
关于 Cloud Studio Cloud Studio 是基于浏览器的集成式开发环境(IDE),为开发者提供了一个永不间断的云端工作站.用户在使用Cloud Studio 时无需安装,随时随地打开浏 ...
- IDEA使用@Autowired注解为什么会提示不建议?
在使用IDEA编写Spring相关的项目时,当在字段上使用@Autowired注解时,总会出现一个波浪线提示:"Field injection is not recommended.&qu ...
- 聊一聊 Go 的内存对齐
前言 在一次工作中,需要使用 Go 调用 DLL 文件,其中就涉及到内存对齐的相关知识,如果自定义的结构体内存布局和所调用的 DLL 结构体内存布局不一致,就会无法正确调用.所以,一旦涉及到较为底层的 ...
- SQL多表查询指南
SQL多表查询指南 在实际的数据库应用中,通常需要查询涉及多个表的数据.SQL提供了多种方法来执行这种多表查询操作. 内连接(INNER JOIN) 内连接是将多个表中满足连接条件的行组合在一起的操作 ...
- gitlab与LDAP 联调
gitlab整理 目录 gitlab整理 1.安装Gitlab依赖包 2.下载,安装 3.配置,访问域名及邮箱 4.初始化,启动 5.访问,以及邮箱测试 5.1汉化 6.问题总结处理 6.1安装时出现 ...
- DevSecOps之应用安全测试工具及选型
上篇文章,有同学私信想了解有哪些DevSecOps工具,这里整理出来,供大家参考(PS: 非专业安全人士,仅从DevOps建设角度,给出自己见解) 软件中的漏洞和弱点很常见:84%的软件漏洞都是利用应 ...
