HanLP — 感知机(Perceptron)

感知机(Perceptron)是一个二类分类的线性分类模型，属于监督式学习算法。最终目的： 将不同的样本分本

感知机饮食了多个权重参数，输入的特征向量先是和对应的权重相乘，再加得到的积相加，然后将加权后的特征值送入激活函数，最后得到输出



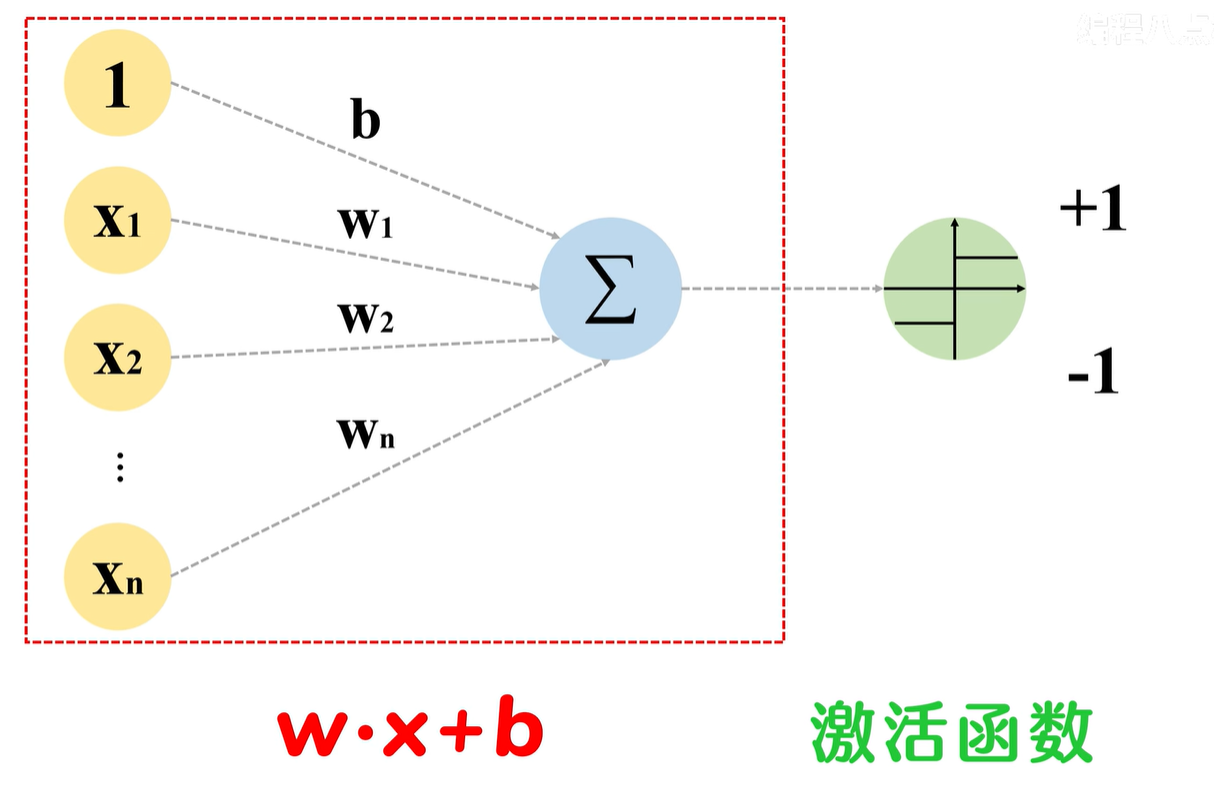
激活函数的前面部分，是线性方程 wx+b

线性方程输出的是连续的值，但对于分类来说，最终需要的类别信息是离散的值，这时候，激活函数就派上用场了，激活函数的存在，是将连续回归值，转变成1 -1 这样的离散值，从而实现类别划分

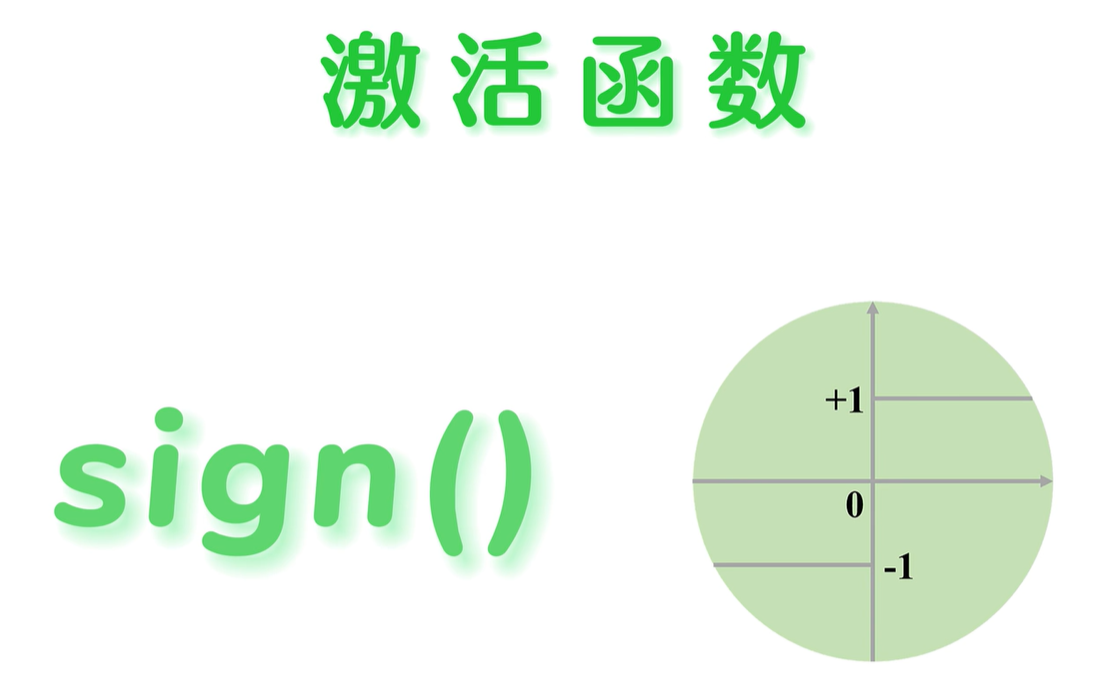
激活函数

激活函数有很多种，在深度学习中，有着非常重要的作用，在感知机中使用的激活函数是 sin(),

假如输入到模型中的是一个二维的特征向量(x1,x2),则整个过程可以表示为如下：



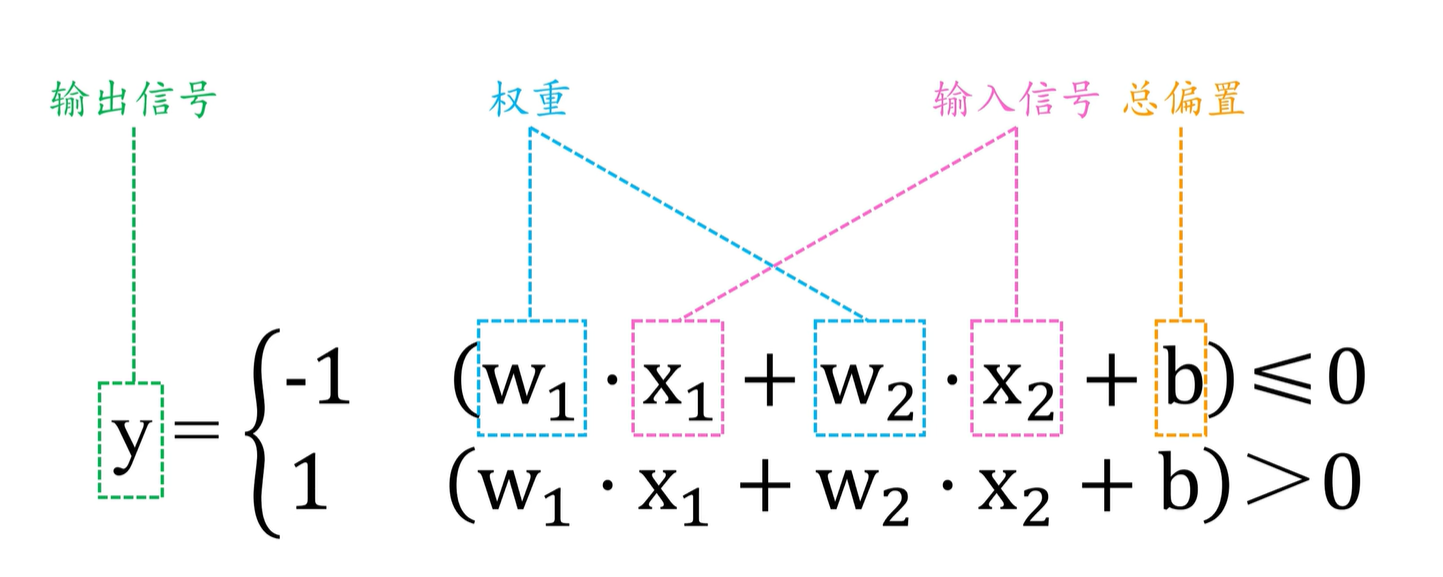
输入的特征向量（x1,x2)先分别和权重(w1,w2)相乘，再将两者相加，最后加上偏置 b ，最终得到的值，和阈值 0 做比较，如果值大于0 则输出1，否则则输出 -1

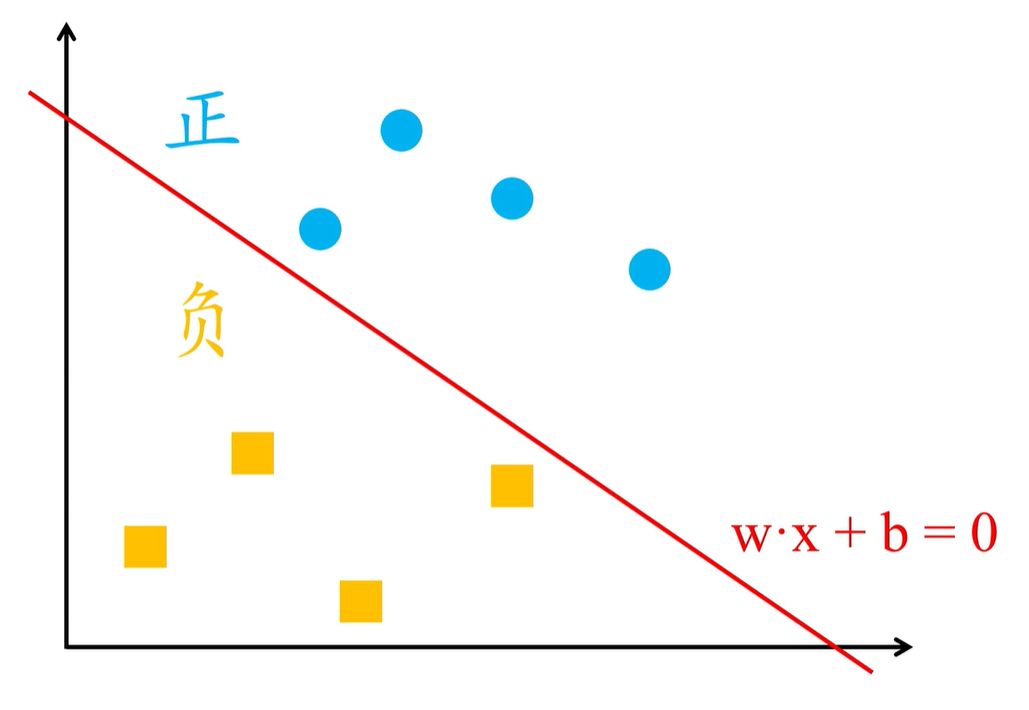
这样一来，就会划分到了线性方程 wx+b=0 两侧的样本，就分成了正、负两类，用感知机进行二分类，需要先找到能够将正、负样本完全区分开的决策函数 wx+b=0，如下图

因此就需要确定一个学习策略，也就是定义一个损失函数，再通过训练样本，通过减小损失值，不断迭代模型参数，最终找到最优参数 w 和 b ，

损失函数的作用： 用来衡量模型的输出结果，和真实结果之间的偏差，然后根据偏差，修正模型，

回归任务



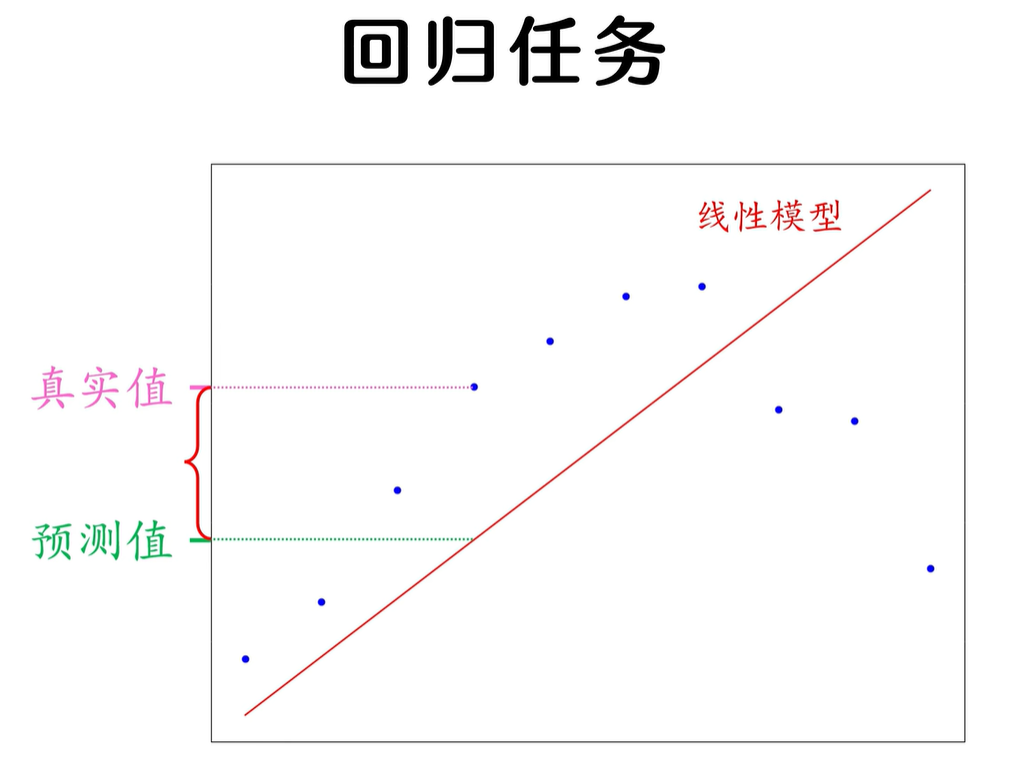
在回归任务中，标签和模型输出都是连续的数值，很容易就能衡量出二者之间的差异。

可对于感知机的分类问题来说，我们又该如何衡量差异呢？一个直观的想法，就是去统计误分类样本的个数作为损失值，误分类的样本个数越多，说明这个该样本空间下的表现越差，但是这样的函数是非连续的，对 w 和 b 不可导，所以我们无法使用这样的损失函数来更新 w 和 b.

为了得到连续可导的损失函数，感知机选择用误分类样本到决策函数的距离，来衡量偏差



这里是单个样本点到决策函数的距离公式

\(\frac {1}{||w||} |w*x_0+b|\)

其中 \(x_0\) 表示样本点的输入 \(||w||\)等于权重向量 \(w\) 的模长 \(||w|| = \sqrt{(w_1^2 + w_2^2 + ... + w_n^2)}\)

对于感知机分类问题来说，可以用 \(-y_0(w*x_0+b)\) 来代替 \(|w*x_0+b|\)

\(y_0\) 表示样本点 \(x_0\) 对应的标签值。

为什么可以这样代替呢？

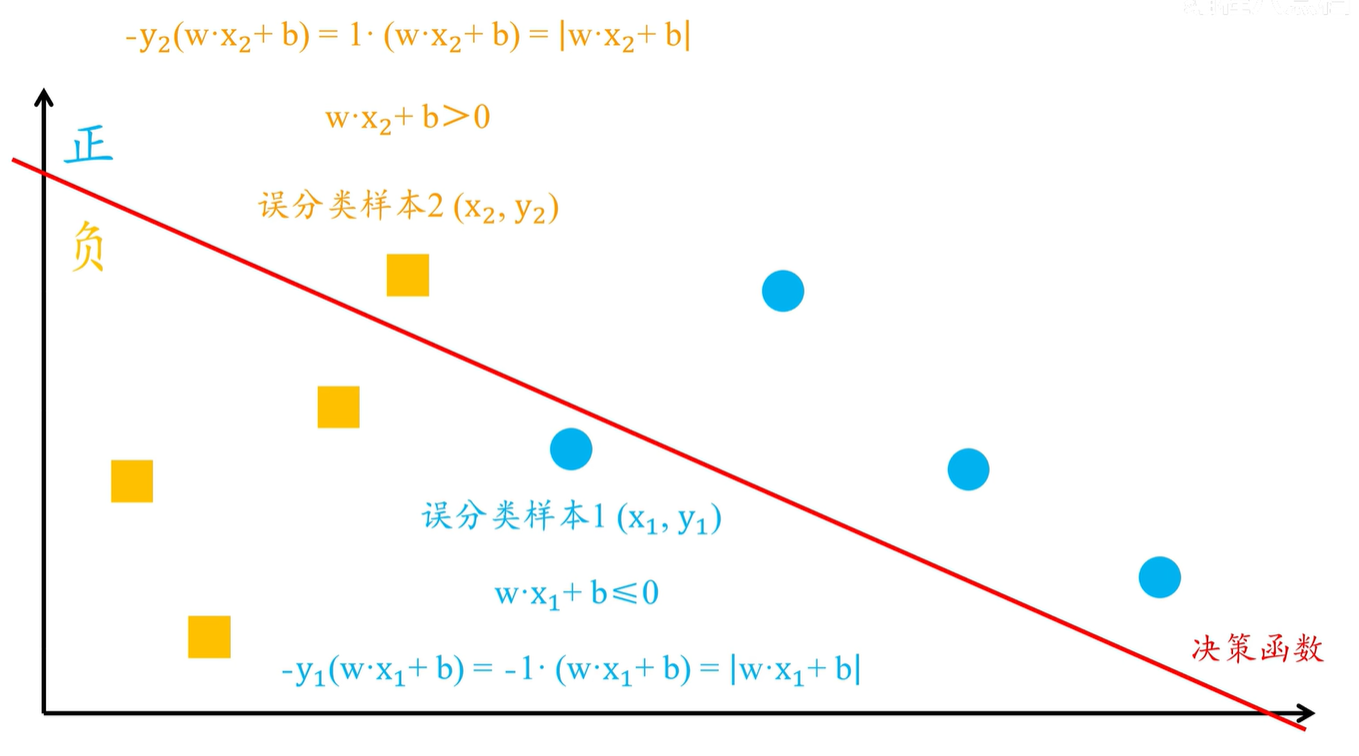
假设有两个误分类样本

样本1 \((x_1,y_1)\) 样本2 $(x_2,y_2) \(，
样本1 的真实类别为正样本，即：\)y_1 = 1$，但是在模型中，样本1 却被误分类为了负样本，也就是计算得到的 \(wx1+b \leq 0\)，那么 \(-y_1(w*x_1+b)=-1(w*x_1+b)\) 最终的结果变成了正值，大小等于 \(|w*x_1+b|\)

样本2 的真实类别为负样本，\(y_2=-1\) 即在模型中被误分类为了正样本。也就是计算得到的 \(w*x_2+b > 0\)，那么 \(-y_2(w*x_2+b)\) 就等于 \(1(w*x_2+b)\) ，结果仍为正值，大小等于 \(|w*x_2+b|\)

因此：所有误分类的样本到决策函数的距离和就可以表示为如下

感知机所关心的，是怎么能将两类样本正确地区分开，对样本点到决策函数距离的大小并不关心，如下图，红线和绿线都能将两类样本正确地区分开，所以对感知机来说，这两条线的分类效果是一样的



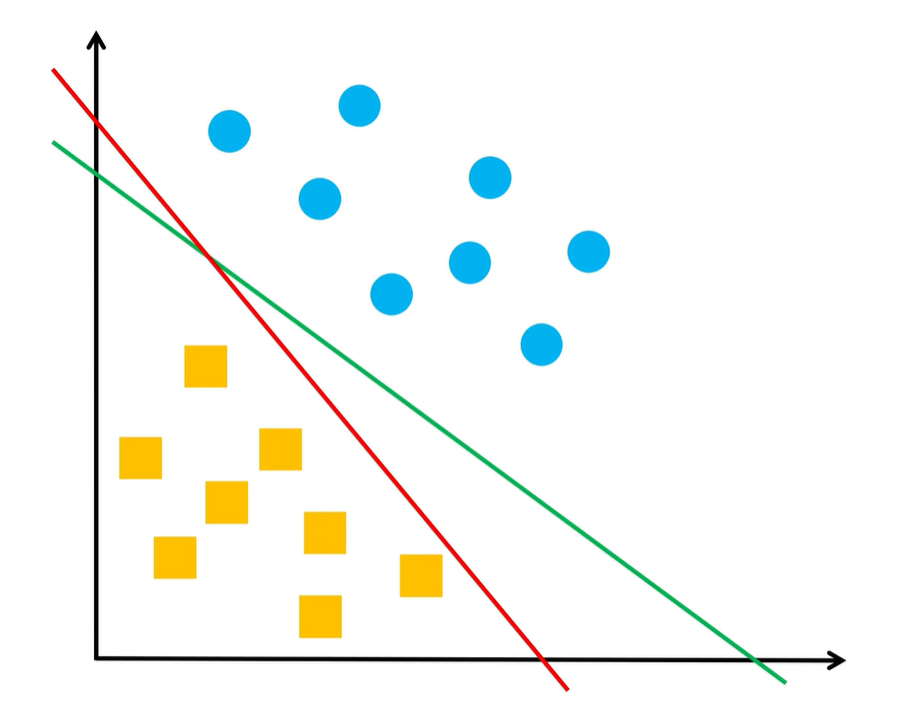
因此，可以把\(\frac {1}{||w||}\) 去掉



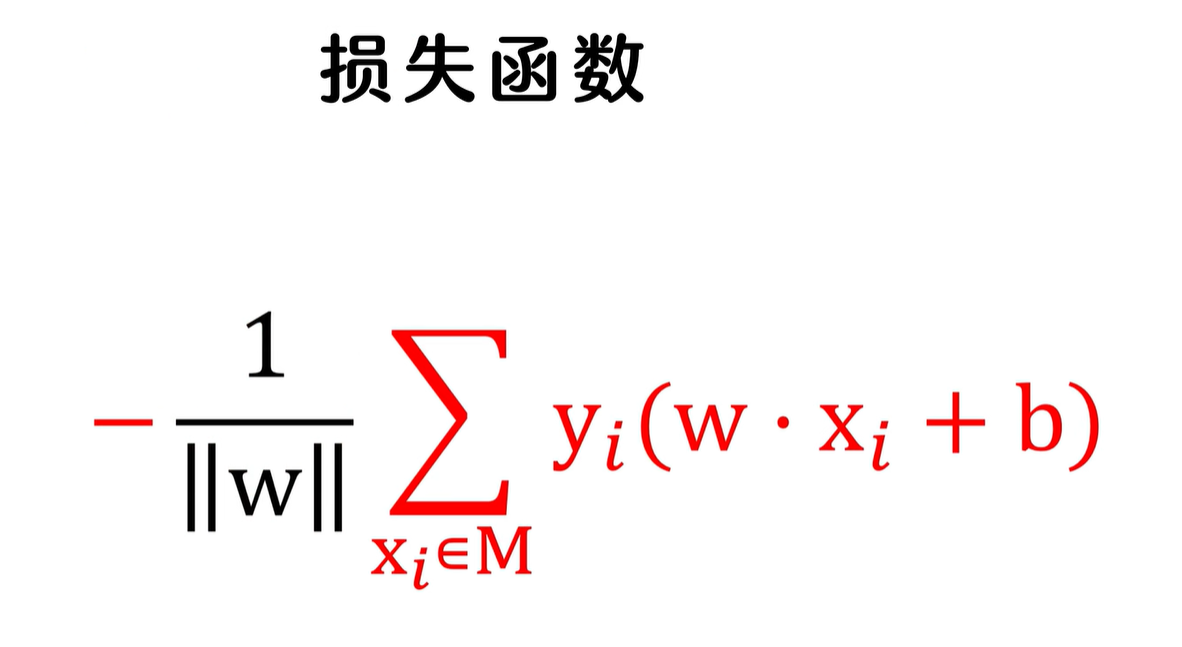
最终，感知机的函数就是 $$ L(w,b) = - \sum_{x_i{\in}M}y_i(w*x_i+b) $$

感知机适用于样本特征简单，且线性可分的二分类问题，因为运算简单，所以计算效率高。

不过在复杂的场景中，感知机往往不能胜任，所以我们在感知机的基础上，又诞生了多层感知机和神经网络

https://www.bilibili.com/video/BV19h4y1w7WL