动物园 $[APIO \ 2007]$

· 题意：

新建的圆形动物园是亚太地区的骄傲。圆形动物园坐落于太平洋的一个小岛上，包含一大圈围栏，每个围栏里有一种动物。如下图所示：

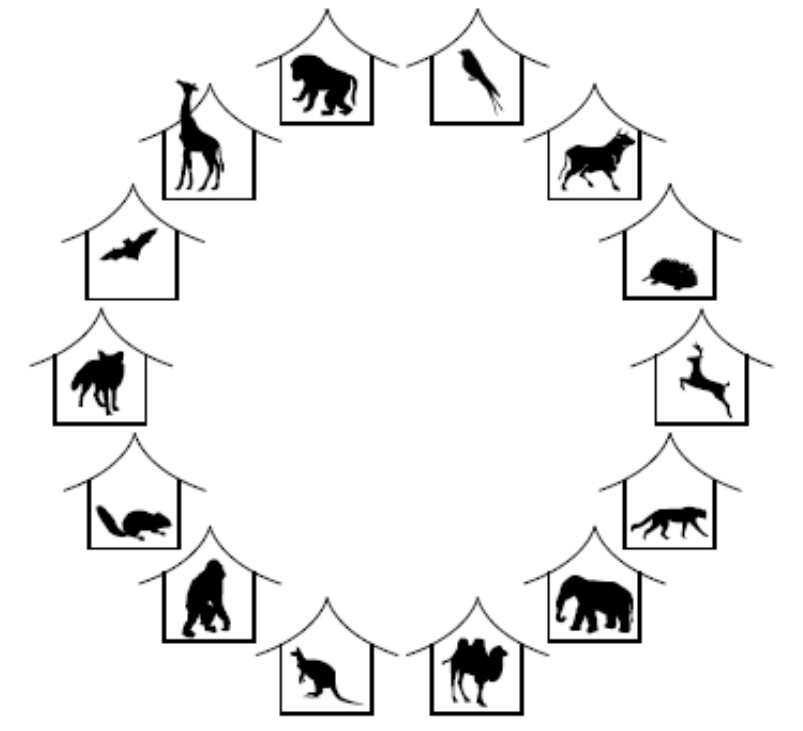
你是动物园的公关主管。你要做的是，让每个参观动物园的游客都尽可能高兴。今天有一群小朋友来到动物园参观，你希望能让他们在动物园度过一段美好的时光。但这并不是一件容易的事.有些小朋友喜欢某些动物，而有些小朋友则害怕某些动物。例如， Alex 喜欢可爱的猴子和考拉，而害怕拥有锋利牙齿的狮子。而 Polly 会因狮子有美丽的鬃毛而喜欢它，但害怕有臭味的考拉。

你可以选择将一些动物从围栏中移走以使得小朋友不会害怕。但你移走的动物也不能太多，否则留给小朋友们观赏的动物就所剩无几了。

每个小朋友站在大围栏圈的外面，可以看到连续的

个围栏。你得到了所有小朋友喜欢和害怕的动物信息。当下面两处情况之一发生时，小朋友就会高兴：

至少有一个他害怕的动物被移走；
至少有一个他喜欢的动物没被移走。

例如，考虑下图中的小朋友和动物：

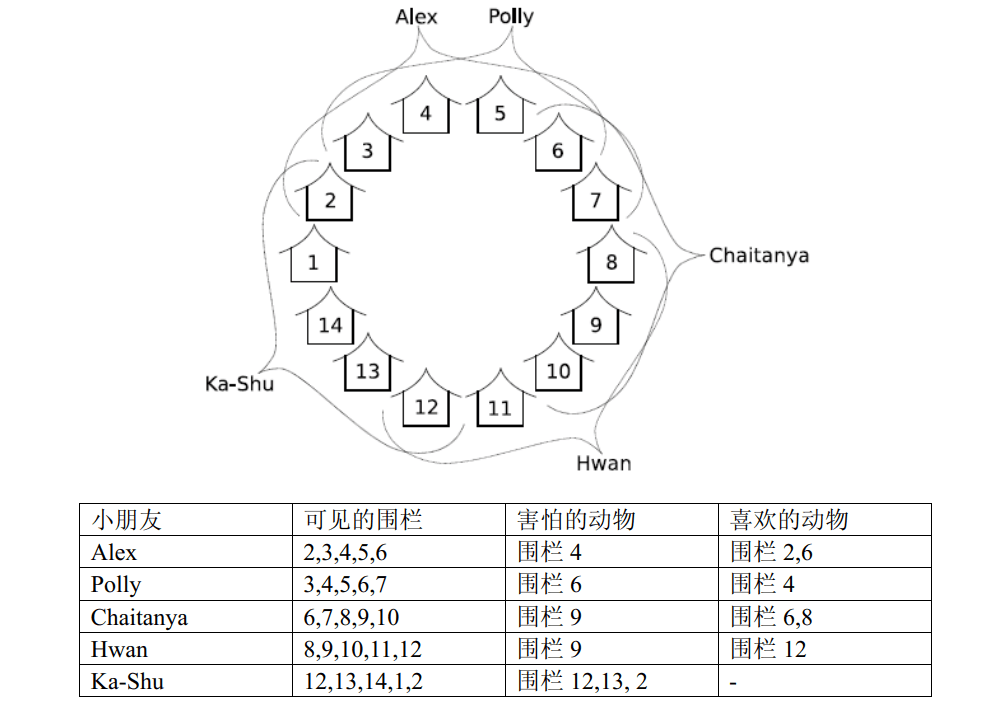
假如你将围栏 $4$ 和 $12$ 的动物移走。Alex 和 Ka-Shu 将很高兴，因为至少有一个他们害怕的动物被移走了。这也会使 Chaitanya 高兴，因为他喜欢的围栏 $6$ 和 $8$中的动物都保留了。但是，Polly 和 Hwan 将不高兴，因为他们看不到任何他们喜欢的动物，而他们害怕的动物都还在。这种安排方式使得三个小朋友高兴。

现在换一种方法，如果你将围栏 $4$ 和 $6$ 中的动物移走，Alex 和 Polly 将很高兴，因为他们害怕的动物被移走了。Chaitanya 也会高兴，虽然他喜欢的动物 $6$ 被移走了，他仍可以看到围栏 $8$ 里面他喜欢的动物。同样的 Hwan 也会因可以看到自己喜欢的动物

而高兴。唯一不高兴的只有 Ka-Shu。

如果你只移走围栏 $13$

中的动物，Ka-Shu 将高兴，因为有一个他害怕的动物被移走了，Alex, Polly, Chaitanya 和 Hwan 也会高兴，因为他们都可以看到至少一个他们喜欢的动物。所以有个小朋友会高兴。这种方法使得了最多的小朋友高兴。

你要求出：最多可以满足的小朋友的数量。

·数据范围

$N \leq 10^4 , C \leq 5 \times 10 ^ 4 $

·输入格式

输入的第一行包含两个整数 $N , C$ ，用空格分隔。 $N$ 是围栏数， $C$ 是小朋友的个数。围栏按照顺时针的方向编号为$1,2,3\dots , N $。

接下来的 $C$行，每行描述一个小朋友的信息，以下面的形式给出：

$E,F,L,X_1,\dots X_n , Y_1,\dots,Y_n$。

其中： $E$ 表示这个小朋友可以看到的第一个围栏的编号，换句话说，该小朋友可以看到的围栏为 $E_1 \dots E_5$ 。注意，如果编号超过 $ n $ 将继续从 $ 1 $ 开始算。

$F$ 表示该小朋友害怕的动物数。

$L$ 表示该小朋友喜欢的动物数。

围栏 $X_i$中包含该小朋友害怕的动物。围栏 $Y_i$中包含该小朋友喜欢的动物。

$X_i , Y_i $ 是两两不同的整数，而且所表示的围栏都是该小朋友可以看到的。

小朋友已经按照他们可以看到的第一个围栏的编号从小到大的顺序排好了（这样最小的 $E$ 对应的小朋友排在第一个，最大的 $E$ 对应的小朋友排在最后一个）。

注意可能有多于一个小朋友对应的 $E$ 是相同的。

·输出格式

仅输出一个数，表示最多可以让多少个小朋友高兴。

·题解

· $DP$

这个题 $GS$ 就 $GS$ 在环上了。

如果以小朋友为基准进行 $DP$ , 由于其并不连续，所以你并没有方法处理环。（其实这里的不可以，意思是 $T$ ）

那么就想一个能处理环还不 $T$ 的算法。

那你的 $DP$ 数组肯定是要开两维，那上面那种情况已经被否决了。

那么你可以这么定义这个 $DP$ :

$DP_{ i , j }$ : $ i $ 表示目前枚举到第 $i$ 个栅栏，其后面的，包括其自身的 $5$ 个数的状态压缩一下成为 $j$ .

那么先挂一下方程：

\[dp_{ i , j } = \max \{ dp_{ i - 1 , ( ( ( 1 << 4 ) - 1 ) \& j ) << 1 } , dp_{ i - 1 , ( ( ( 1 << 4 ) - 1 ) \& j ) << 1 | 1 } \} + b_{ i , j }
\]

这个 $ b_{ i , j } $ 的意思是，在从 $i$ 开始， $j$ 为状态下，可以让多少个小朋友高兴。存在之的充分必要条件是此点上有小朋友的观察。

那么这个一堆的下标是表示什么的呢？

显然，$ 2 ^ 4 - 1 $ 是 $\left(1111\right)_2$ 你拿目前的状态 $\&$ 这个，相当于未保存第五位的数，即你因为 $i$ 比 $i-1$ 多 $1$ 而末位多出的一位。

你现在左移一位，那么就使 $j$ 的第四位，变成了最高位。

其实仔细的想一想，其实很有道理。你从 $ i $ 从左往右数的第 $ 4 $ 个，不就是 $ i - 1 $ 从左往右选的第 $ 5 $ 个数。

在最低位 $ 0 $ $| \ 1 $ , 就是 $ i - 1 $ 是 $ 1 $ , 不动就是 $ 0 $ .

在原来状态得到的最大值，加上此位置小盆友的快乐数，即此状态下的最大答案。

子问题 $1$ ：如何预处理 $b$ 数组

因为只有当 $ i $ 上有小朋友的观察时才有 $b$ 的值 .

那么就好说了，在输入小朋友时，你用两个变量；

喜欢的，用 $love$ 或起来；害怕的也是，用 $ fear $ 。

枚举一遍状态 $ j $ , 当：

$ j 按位与 love $ 为真或 $ ( $ $ \ j取反 \ 按位与 \ fear )$ 为真，即可累计答案。

（这个地方好想一些，挺巧妙的）。

子问题 $2$ ：如何处理环

考虑什么情况下可以使答案合法：

$n$ 的状态的后四位和 $1$ 的状态的前四位相同时。

那么如何处理得到这种情况呢？

我们可以定义一个 $n$ 的镜像点，视为 $dp_{ 0 , j }$ 。表示第 $n$ 个点 $j$ 状态。

使从此点开始 $DP$ ，那么使其他的 $dp_{ 0 , k } ( k \in A = \{ 1, \dots , 31 | k \ne j \} )$

均为负无穷，此时对于后面的加减，可以抵消其作用。

最后输出 $dp_{ n , j }$ 的最大值即可。

· $code$

有些东西没有用，可以恰当的删一下。

点击查看代码

#include<bits/stdc++.h>

const int C = 5e4 + 100 ;

const int N = 1e4 + 100 ;

const int State = ( 1 << 5 ) - 1 ;

using namespace std ;

int n , m ;

class node

{

    public:

        int left , right ;

        int num_fond , num_afraid ;

        int fondations[ 10 ] , afraid[ 10 ] ;

} a[ C ] ;

int dp[ N ][ State + 1 ] ;

int b[ N ][ State + 1 ] ;

int papa = 0 , aiai = 0 ;

signed main ( )

{

    ios::sync_with_stdio( 0 ) ;

    cin.tie( 0 ) ; cout.tie( 0 ) ;

    cin >> n >> m ;

    for ( int i = 1 ; i <= m ; ++ i )

    {

        cin >> a[ i ].left ;

        papa = 0 ; aiai = 0 ;

        cin >> a[ i ].num_afraid >> a[ i ].num_fond ;

        for ( int j = 1 ; j <= a[ i ].num_afraid ; ++ j )

        {

            cin >> a[ i ].afraid[ j ] ;

            int pp = ( a[ i ].afraid[ j ] - a[ i ].left + n ) % n ;

            papa |= ( 1 << pp ) ;

        }

        for ( int j = 1 ; j <= a[ i ].num_fond ; ++ j )

        {

            cin >> a[ i ].fondations[ j ] ;

            int pp = ( a[ i ].fondations[ j ] - a[ i ].left + n ) % n ;

            aiai |= ( 1 << pp ) ;

        }

        for ( int j = 0 ; j <= State ; ++ j )

        {

            if( ( j & papa ) || ( ( ~ j ) & aiai ) )

            {

                b[ a[ i ].left ][ j ] ++ ;

            }

        }

    }

    int ans = -114514 ;

    for ( int kala = 0 ; kala <= State ; ++ kala )

    {

        memset( dp[ 0 ] , 128 , sizeof ( dp[ 0 ] ) ) ;

        dp[ 0 ][ kala ] = 0 ;

        for ( int i = 1 ; i <= n ; ++ i )

        {

            for ( int j = 0 ; j <= State ; ++ j )

            {

                dp[ i ][ j ] = max ( dp[ i - 1 ][ ( ( j & ( 15 ) ) << 1 ) ] , dp[ i - 1 ][ ( ( j & ( ( 15 ) ) ) << 1 | 1 ) ] ) + b[ i ][ j ] ;

            }

        }

        ans = max( ans , dp[ n ][ kala ] ) ;

    }

    cout << ans ;

}

·结尾撒花 $\color{pink}✿✿ヽ(°▽°)ノ✿$