CF1271E Common Number

数学+二分

连续打了3场$codeforces$，深深的被各种模拟贪心分类讨论的$C$，$D$题给恶心到了

还有永远看到题一脸懵的$B$题

---

首先考虑画出不同函数值迭代转移的关系，要注意考虑连边是否能成立，也就是满不满足函数的定义域

 

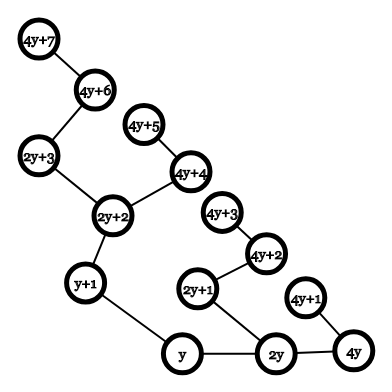
首先观察上图，可以发现如果$y$是偶数，节点$y$的左子树存在

但如果$y$是奇数，节点$y$的左子树不存在，因为$y+1$是偶数，不满足$f(x)=x-1$的定义域

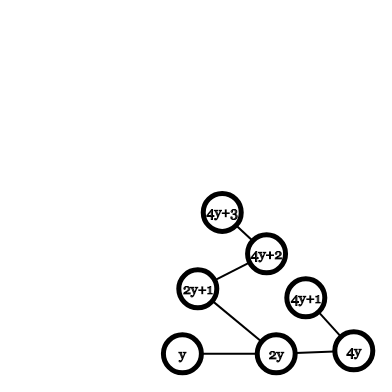
并且右子树的所有节点都存在，因为都是奇数，如下图

那么现在统计一个定值$y$在$1-n$中经过$y$的$path$数，就是以y为根这棵树结点值小于等于n的节点数

观察可以发现，这些节点的值有规律

对于$2^{k}y$级别，树上的范围为$2^{k}y$到$2^{k}y+2^{k+1}-1$

那么可以在$log$的时间求出来

奇数的也是同理，$2^{k}y$到$2^{k}y+2^{k}-1$

但题目要求的是最大的$y$

那么可以分奇数偶数分别二分求解

 1 #include <bits/stdc++.h>
 2 #define ll unsigned long long
 3 #define inf (int)1e9
 4 #define m_k make_pair
 5 using namespace std;
 6 ll n,k,z[63],ans;
 7 bool check(ll mid)
 8 {
 9     if (mid==1)
10       return 1;
11     ll cnt=0;
12     if (mid%2==1)
13     {
14         for (int i=0;i<=62;i++)
15         {
16             if (z[i]*mid>n)
17               break;
18             if (z[i]*mid+z[i]-1<n)
19               cnt+=z[i];
20             else
21             {
22                 cnt+=n-z[i]*mid+1;
23                 break;
24             }
25         }
26     }
27     else
28     {
29         for (int i=0;i<=62;i++)
30         {
31             if (z[i]*mid>n)
32               break;
33             if (z[i]*mid+z[i+1]-1<n)
34               cnt+=z[i+1];
35             else
36             {
37                 cnt+=n-z[i]*mid+1;
38                 break;
39             }
40         }
41     }
42     if (cnt>=k)
43       return 1;
44     else
45       return 0;
46 }
47 int main()
48 {
49     scanf("%lld%lld",&n,&k);
50     if (k==n)
51     {
52         printf("1\n");
53         return 0;
54     }
55     z[0]=1;
56     for (int i=1;i<=62;i++)
57       z[i]=z[i-1]*2;
58     ll l,r;
59     l=0;r=(n-1)/2;
60     while (l<r)
61     {
62         ll mid=l+((r-l+1)>>1);
63         if (check(2*mid+1))
64           l=mid;
65         else
66           r=mid-1;
67     }
68     ans=2*l+1;
69     l=0;r=n/2;
70     while (l<r)
71     {
72         ll mid=l+((r-l+1)>>1);
73         if (check(2*mid))
74           l=mid;
75         else
76           r=mid-1;
77     }
78     ans=max(ans,2*l);
79     printf("%lld\n",ans);
80 }