贝塞尔曲线在Unity中的应用

前言：国庆放假后基本整个人的散掉了。加之种种原因，没时间没心情写博客。最近研究了一下3d的一些效果。其中有类似翻书撕纸的操作，可是一个panel怎么由平整的变成弯曲的呢？

两点可以确定一条直线，三点可以实现一条曲线。其实曲线按照更小的长度来看的话，也是很多段直线构成的。那么三点确定一条曲线的插值运算，就是贝塞尔曲线。今天用Unity实现一阶贝塞尔和二阶贝塞尔。顺便谈谈Unity的Mesh。

一阶贝塞尔：

Unity新建三个cube，摆放在同一个平面内（xy，xz，yz）都行，然后位置不同即可。编写脚本Beizer

public class Beizer : MonoBehaviour
{
    public Transform p0, p1, p2;
    [Range(0,1)]
    public float t;
    // Start is called before the first frame update
    void OnValidate()
    {
        Vector3 temp = p0.position + (p1.position - p0.position) * t;
        p2.position = temp;
    }

    private void Start()
    {

    }

    // Update is called once per frame
    void Update()
    {
        Vector3 temp = p0.position + (p1.position - p0.position) * t;
        p2.position = temp;

    }
}

当t的值为1时，p2的位置为p1的位置（重合了）；

当t的值为0时，p2的位置在p0的位置上（重合了）；

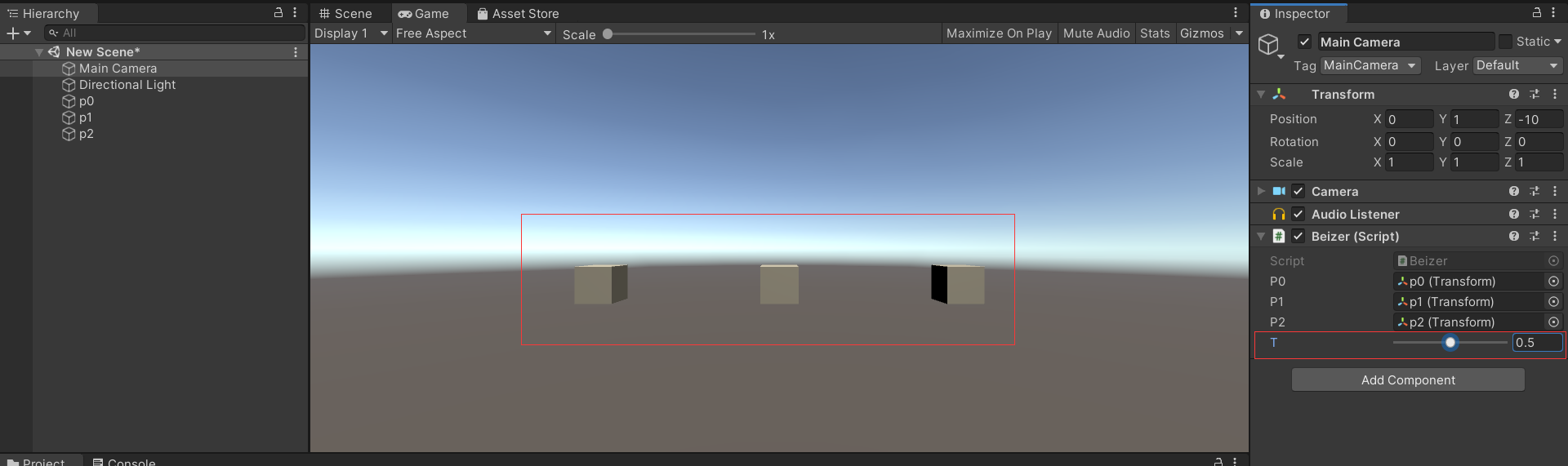
当t的值为0.5时，p2的位置在p0与p1的中间；以上就是一阶贝塞尔的内容。其公式为：B(t)=p0+(p1-p0)*t；

二阶贝塞尔：

Unity同样使用刚刚的场景。只不过p2的位置可以调整下y轴，然后使用LineRender来可视化。

public class Beizer2 : MonoBehaviour
{
    public Transform p0, p1, p2;
    public LineRenderer line;

    public int posCount;

    private void OnValidate()
    {
        line.startWidth = 1;
        line.endWidth = 1;
        line.startColor = Color.red;
        line.endColor = Color.red;
        line.positionCount = posCount;
        Draw();
    }
    // Start is called before the first frame update
    void Start()
    {
        line.startWidth = 1;
        line.endWidth = 1;
        line.startColor = Color.red;
        line.endColor = Color.red;
        line.positionCount = posCount;
    }

    // Update is called once per frame
    void Update()
    {
        Draw();
    }

    void Draw()
    {
        for (int i = 0; i < posCount; i++)
        {
            float tempT = (1f / (float)posCount) * i;
            Vector3 temp = Calculate(tempT, p0.position, p1.position, p2.position);
            line.SetPosition(i, temp);
        }
    }

    Vector3 Calculate(float tValue,Vector3 v0,Vector3 v1,Vector3 v2)
    {
        return Mathf.Pow(1 - tValue, 2) * v0 + 2 * tValue * (1 - tValue) * v1 + Mathf.Pow(tValue, 2) * v2;
    }
}

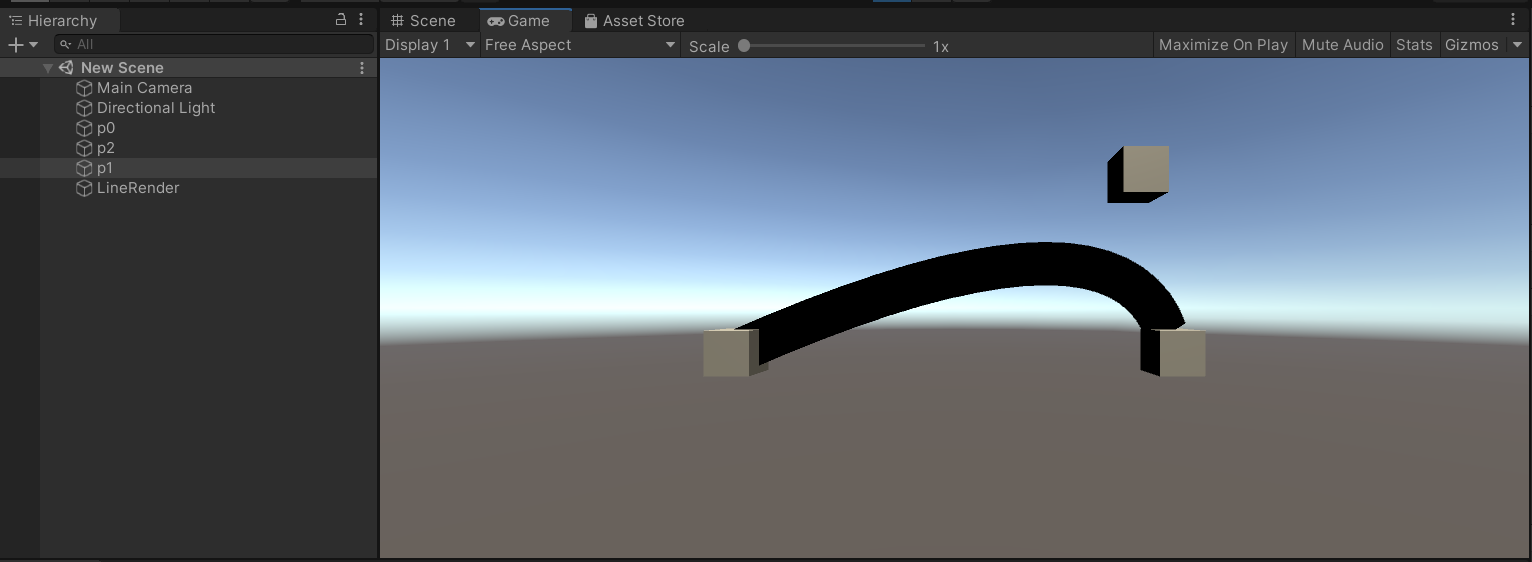
尝试拖动中间那个Cube，可以看见这条曲线也会随之发生变化。

二阶贝塞尔公式：B2(t)=(1 - t)^2 * p0 + 2 * t * (1 - t) * p1 + (t) ^2* p2;

上面说完，就说说开头提到的问题，如何让一个panel变成弯曲的？刚开始我直接傻掉了。后来才知道可以改变Mesh，自定义mesh，再渲染。mesh的各个顶点是用一个Vecter3数组保存的，如果我们直接修改各个顶点的位置信息，再渲染，就会改变mesh的形状，从而显示出各种形状。我们把mesh数组的每一行开头看作是一个点，那么合起来就是一条线，只需把每行的y轴用贝塞尔曲线公式算出就行了。xz轴不用改变，这样就是弯曲的了。我还做了一个翻动动画，整个过程的弯曲程度是通过贝塞尔曲线插值运算出来的。

mesh这个东西很奇妙，主要包括顶点、三角片、uv，完全可以定义出自己想要的mesh。后来的无限分割模型其实也是这个思路，重新生成mesh，只不过这个就很难了，我用的是Unity商城里的切割插件。（其实我不太能搞懂mesh，目前只会用，所以不能再细说下去了）