【LeetCode动态规划#05】背包问题的理论分析（基于代码随想录的个人理解，多图）

背包问题

问题描述

背包问题是一系列问题的统称，具体包括：01背包、完全背包、多重背包、分组背包等（仅需掌握前两种，后面的为竞赛级题目）

下面来研究01背包

实际上即使是最经典的01背包，也不会直接出现在题目中，一般是融入到其他的题目背景中再考察

因为是学习原理，所以先跳过最原始的问题模板来学。

01背包的原始题意是：（标准的背包问题）

有n件物品和一个最多能背重量为 w 的背包。第 i 件物品的重量是 weight[i] ，得到的价值是 value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

（01背包问题可以使用暴力解法，每一件物品其实只有两个状态，取或者不取，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是O(2^n)，这里的n表示物品数量。因为暴力搜索的时间复杂度是指数级别的，所以才需要通过dp来进行优化）

根据上面的描述可以举出以下例子

二维dp数组01背包

背包最大重量为4。

物品为：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

问背包能背的物品最大价值是多少？

五部曲分析一波

五步走

1、确定dp数组含义

该问题中的dp数组应该是二维的，所以先定义一个dp[i][j]

该数组的含义是什么？

含义：任取编号（下标）为[0, i]之间的物品放进容量为j的背包里

2、确定递推公式

确定递推公式之前，要明确dp[i][j]可以由哪几个方向推导出

当前背包的状态取决于放不放物品i，下面分别讨论

（1）不放物品i

dp[i - 1][j]

（2）放物品i

dp[i - 1][j - weight[i]] + value[i] （物品i的价值）

我来解释一下上面的式子是什么意思

先回顾一下dp[i][j]的含义：从下标为[0, i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

那么可以有上述两个方向推出来dp[i][j]

情况1：不放物品i。此时我们已经认为物品i不会被放到背包中，那么根据dp[i][j]的定义，任取物品的范围应该变成[0, i-1]

也就是从下标为[0, i-1]的物品里任意取，放进容量为j的背包，价值总和最大是多少，即dp[i - 1][j]

再看情况2：放物品i。因为要放物品i，那就不需要再遍历到i了（相当于已经放入背包的东西下次就不遍历了）

根据dp[i][j]的定义，任取物品的范围也应该变成[0, i-1]

但是，因为情况2是要将物品i放入背包，此时背包的容量也要发生变化

根据dp[i][j]的定义，背包的容量应该要减去物品i的重量 weight[i] ，即dp[i - 1][j - weight[i]]

此时dp[i - 1][j - weight[i]]只是做好了准备放入物品i的工作，实际上物品i并没有放入，因此该式子的含义是：背包容量为j - weight[i]的时候不放物品i的最大价值

所以要再加上物品i本身的价值 value[i] ，才能求出背包放物品i得到的最大价值

即：dp[i - 1][j - weight[i]] + value[i]

根据dp[i][j]的定义，我们最后要求价值总和最大物品放入方式

因此递推公式应该是： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

从不放物品i和放物品i两个方向往dp[i][j]推，取最后结果最大的那种方式（即最优的方式）

3、确定dp数组初始化方式

可以把dp数组试着画出来，然后假设要求其中一个位置，思考可以从哪个方向将其推出，而这些方向最开始又是由哪些方向推得的，进而确定dp数组中需要初始化的部分

将本题的dp数组画出来如下：

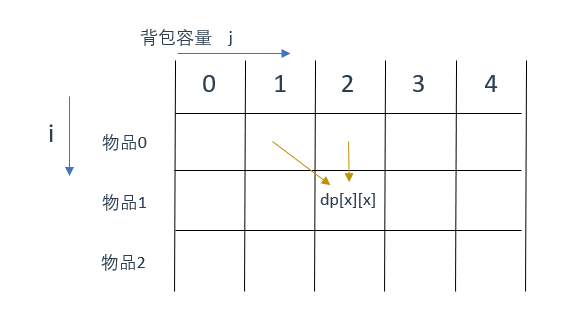
假设有一个要求的元素dp[x][x]，根据前面对递推公式的讨论可知，该元素一定是由两个方向推过来求得的。

也就是情况1、情况2，那么对应到图中就是从上到下推过来的，是情况1（dp[i - 1][j]）

情况2（dp[i - 1][j - weight[i]]）在图中体现得不是十分确定，但是大致方向是从左上角往下推过来的

这两个方向的源头分别指向绿色区域和橙色区域

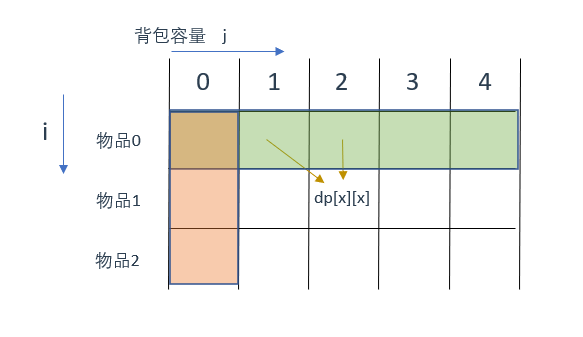
那么这两个区域就是要初始化的区域，怎么初始化呢？

先说橙色区域，从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。

所以橙色区域区域需要初始化为0

再说绿色区域，状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出 i 是由 i-1 推导出来，那么 i 为 0 的时候就一定要初始化

dp[0][j]，即：i 为0，存放编号0 的物品的时候，各个容量的背包所能存放的最大价值。

很明显当 j < weight[0]的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小。

当j >= weight[0]时，dp[0][j] 应该是 value[0] ，因为背包容量放足够放编号0物品。

两个区域的初始化情况对应到图中如下：

初始化代码：

for (int j = 0 ; j < weight[0]; j++) { //橙色区域

    dp[0][j] = 0;

}

// 正序遍历

for (int j = weight[0]; j <= bagweight; j++) {//绿色区域

    dp[0][j] = value[0];

}

以上两个区域实际上属于“含0下标区域”，其他的“非0下标区域”也需要初始化（没想清楚为什么有时要初始化完整个dp数组，有时又不用）

“非0下标区域”初始化为任何值都可以

还是拿前面的图来看

以dp[x][x]这个位置为例，其初始化成100、200都无所谓，因为这个位置的dp值是由其上面和左上两个方向上的情况推导出来的，只取决于这里个方向最开始的初始化值。

（例如dp[x][x]这里初始化为100，我从上面推导下来之后会用推导值将100覆盖）

4、确定遍历方式

该问题中dp数组有两个维度：物品、背包容量，先遍历哪个呢？

直接说结论，都行，但是先遍历物品更好理解

（具体看代码随想录解释）

两种过程的图如下：

（这里需要重申一下背包问题的条件：每个物品只能用一次，要求的是怎么装背包里的价值最大）

先遍历物品再遍历背包容量（固定物品编号，遍历背包容量）

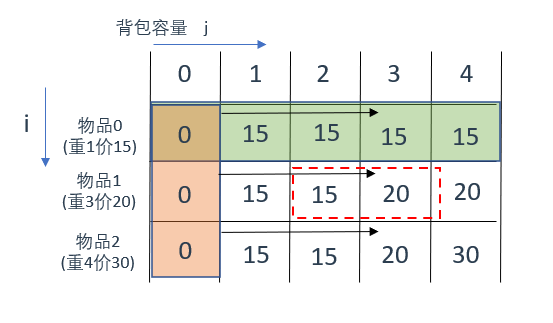
挑一个节点来说一下（图中的红框部分），此时的遍历顺序是先物后包，物品1(重3价20)在0~4种容量中放置的结果如图所示

因为固定了物品1，此时背包容量为0、1、2的情况都是放不下物品1的（又也放不下物品3），所以只能放物品0（此为最佳选择）

当遍历到背包容量为3时，可以放下物品1了，那此处的最佳选择就是放一个物品1，所以此处的dp数组值变为20

其余位置分析方法同理

先遍历背包容量再遍历物品（固定背包容量，遍历物品编号）

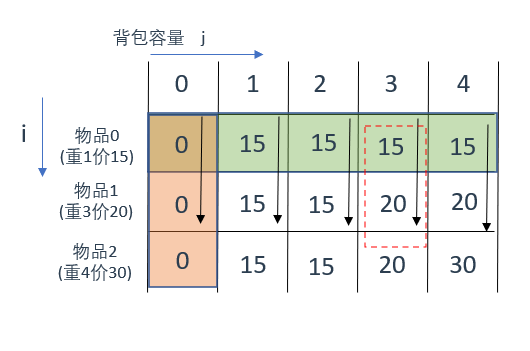
有了前面的例子，这里就很好理解了，就是从上往下遍历，固定住当前背包的容量，遍历物品，看看能不能放入，能放的话最优选择应该放哪个

还是拿红框部分来说，此时背包容量固定为3

第一次遍历，物品0可以装下，此时最优选择就是放物品0，背包总价是15；

第二次遍历，物品1可以装下，此时最优选择就是放物品1，背包总价是20；

第二次遍历，物品2装不下，此时最优选择就是放物品1，背包总价还是20；

其余位置分析方法同理

完整c++测试代码（卡哥）

void test_2_wei_bag_problem1() {

    vector<int> weight = {1, 3, 4};

    vector<int> value = {15, 20, 30};

    int bagweight = 4;

    // 二维数组

    vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));

    // 初始化

    for (int j = weight[0]; j <= bagweight; j++) {

        dp[0][j] = value[0];

    }

    // weight数组的大小 就是物品个数

    for(int i = 1; i < weight.size(); i++) { // 遍历物品

        for(int j = 0; j <= bagweight; j++) { // 遍历背包容量

            if (j < weight[i]) dp[i][j] = dp[i - 1][j];

            else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

        }

    }

    cout << dp[weight.size() - 1][bagweight] << endl;

}

int main() {

    test_2_wei_bag_problem1();

}