【LeetCode练习题】Unique Paths

Unique Paths

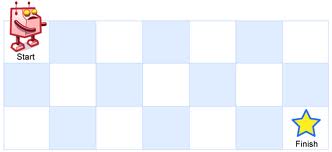
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

Above is a 3 x 7 grid. How many possible unique paths are there?

Note:m and n will be at most 100.

计算从起点到终点的最短距离。

（动态规划的题目，没错我开始学DP了……）

解题思路：

因为题目中提到了每一次只能向右或者向下移动，所以以终点为例，记为C（3,7），则能到达终点的点分别是A（3,6）和B（2,7），即从起点到达终点的路径数等于从起点到达A点和B点路径数量的和。C = A + B。

有了这一点，接下来就很好想了。

这一题说起来是动态规划，其实还是算挺简单的，他有好几种做法。

首先我刚刚看到这一题的时候，想法是这样的：

动态创建一个m行n列的数组p，存储每一个位置到起点的路径数量。

因为所有与起点start同一行上的点和同一列上的点到起点的路径只有一条，就是一条直线。所以p[0][0~n-1]和p[0~m-1][0]全部置为1。然后根据每一个位置等于它左边的值与上边的值的和就很好计算了。

比较好的一点是，这种看起来低端不上档次的方法还避免了动态规划方法的重复计算问题。

代码如下：

class Solution {
public:
    int uniquePaths(int m, int n) {
        if(m ==  || n == )
            return ;
        //动态创建二维数组
        int **p;
        p = new int*[m];
        for(int i = ; i < m; i++){
            p[i] = new int[n];
        }
        for(int i = ; i < m; i++)
            for(int j = ; j < n;j++)
                p[i][j] = ;

        //初始化第一行为1
        for(int i = ; i < n; i++){
            p[][i] = ;
        }
        //初始化第一列为1
        for(int i = ; i < m; i++){
            p[i][] = ;
        }
        //从第二行第二列开始计算每一格
        for(int i = ; i < m; i++){
            for(int j = ; j < n; j++){
                p[i][j] = p[i][j-] + p[i-][j];
            }
        }

        int ret = p[m-][n-];

        for(int i = ; i < m; i++)
            delete[] p[i];
        delete[] p;

        return ret;
    }
};

接下来就是高端大气上档次滴采用递归的动态规划的解法了。或者叫做回溯法。

如果是这样子写：

class Solution {
public:
    int uniquePaths(int m, int n) {
        if(m ==  || n == )
            return ;
        return uniquePaths(m,n-)+uniquePaths(m-,n);
    }
};

那么提交上去……

显示 超时 ！

原因很简单，因为存在大量的重复计算！

所以我们还是需要维护一个二维数组来避免同一个位置的值重复计算。当某个值已经被计算出来，下次再用到这个值时，直接取就可以不用再去计算了。

所以代码变成了这样子：

const int M_MAX = ;
const int N_MAX = ;

class Solution {

public:
    int uniquePaths(int m, int n) {
        int mat[M_MAX+][N_MAX+];
        for(int i = ; i < M_MAX+; i++){
            for(int j = ; j < N_MAX+; j++){
                mat[i][j] = -;
            }
        }
        return backtrack(m,n,mat);
    }

    int backtrack(int m,int n,int mat[][N_MAX+]){
        if(m ==  || n == )
            return ;
        if(mat[m][n-] == -)
            mat[m][n-] = backtrack(m,n-,mat);
        if(mat[m-][n] == -)
            mat[m-][n] = backtrack(m-,n,mat);
        return mat[m][n-] + mat[m-][n];
    }
};

我们知道以上的空间复杂度是 O(m * n)。

接下来的这种动态规划的空间复杂度是O(min(m , n))。

非常有意思。

public static int uniquePathsDP(int m, int n){
    int x = Math.min(m, n);
    int y = Math.max(m, n);
    int[] ret = new int[x];

    for(int i = ; i < x; i++)
        ret[i] = ;

    for(int i = ; i < y; i++)
        for(int j = ; j < x; j++)
        {
            ret[j] += ret[j - ];
        }

    return ret[x - ];
}

注：

动态创建二维数组的代码，因为我总是记不住，就此记录：

char **a;
a = new char* [m];//分配指针数组
for(int i=; i<m; i++)
{
    a[i] = new char[n];//分配每个指针所指向的数组
}

printf("%d\n", sizeof(a));//4，指针
printf("%d\n", sizeof(a[]));//4，指针

for(i=; i<m; i++)
    delete[] a[i];
delete[] a;