机器学习实战笔记-11-Apriori与FP-Growth算法

Apriori算法

1. 优点：易编码实现；缺点：大数据集上较慢；适用于：数值型或标称型数据。

2. 关联分析：寻找频繁项集(经常出现在一起的物品的集合)或关联规则(两种物品之间的关联关系)。

3. 概念：支持度：数据集中包含某项集的记录所占的比例P(A)；可信度(置信度)：对某个关联规则\(A\rightarrow B\)，\(\frac{P\left( \text{AB} \right)}{P(A)}\)表示。
   
   
   
   

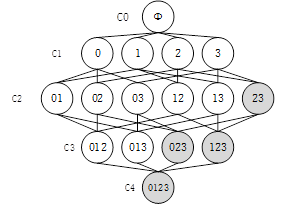
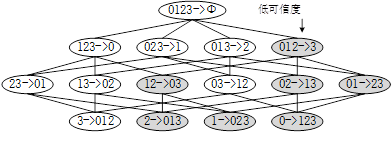
4. Apriori原理：频繁项集的子集一定是频繁项集，非频繁项集的超集一定是非频繁项集。

   Apriori算法(目的:发现频繁项集)，辅助函数”检查是否频繁项集”伪代码：

   对数据集中每条交易记录transaction：
   对每个候选项集can：
       检查can是否是tran的子集：
       如果是，则增加can项集的计数值
   对每个候选项集can：
       如果支持度不低于最小值(参数),则保留该项集
   返回所有频繁项集列表，支持度词典
   

   Apriori算法(目的:发现频繁项集),伪代码：

   生成C1项集(只有1个元素的项集)
   利用辅助函数过滤掉C1的非频繁项集
   当项集列表$C_{k - 1}$中项集的个数大于0时：
       构建候选项集的列表$C_{k}$(用$C_{k - 1}$构建$C_{k}$：$C_{k -1}$中项集两两比较，如果前$k -2$个元素均一样，则可以合并为一个大小为$k$的项集)
       检查数据集以确认每个$C_{k}$的项集均为频繁的
       保存该频繁项集列表$C_{k}$
       K++
   

5. FP-growth算法(Frequency
   
   Pattern-Growth)：较Apriori更快，但实现较之困难，适用于标称型。

   第一次遍历数据集统计每个元素项的频率>>去掉小于最小支持度的元素项>>按频率(从大到小)对元素项进行排序>>按该顺序对数据集中各条数据进行排序>>|构建FP树|读入每个项集并将其添加到一条已存在的路径中，如果该路径不存在，则创建一条新路径>>抽取条件模式基(以所查元素为结尾的路径的集合)>>以条件模式基为每一个元素项创建一个条件FP树(每步进行最小支持度的检查)>>在该条件FP树中的两两组合项集挖掘条件FP树，即重复以上两步直到条件树没有元素为止。