ODEINT 求解常微分方程(3）

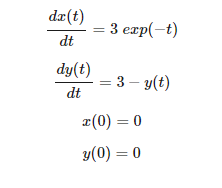
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# function that returns dz/dt
def model(z,t):
    dxdt = 3.0 * np.exp(-t)
    dydt = -z[1] + 3
    dzdt = [dxdt,dydt]
    return dzdt

# initial condition
z0 = [0,0]

# time points
t = np.linspace(0,5)

# solve ODE
z = odeint(model,z0,t)

# plot results
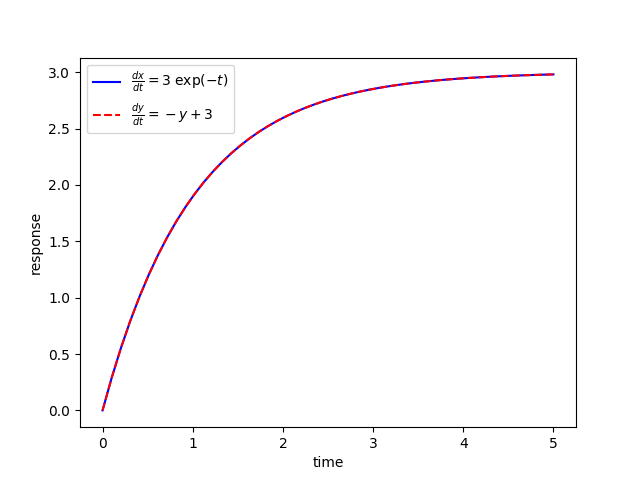
plt.plot(t,z[:,0],'b-',label=r'$\frac{dx}{dt}=3 \; \exp(-t)$')
plt.plot(t,z[:,1],'r--',label=r'$\frac{dy}{dt}=-y+3$')
plt.ylabel('response')
plt.xlabel('time')
plt.legend(loc='best')
plt.show()