CTR学习笔记&代码实现1-深度学习的前奏LR->FFM

CTR学习笔记系列的第一篇，总结在深度模型称王之前经典LR，FM, FFM模型，这些经典模型后续也作为组件用于各个深度模型。模型分别用自定义Keras Layer和estimator来实现，哈哈一个是旧爱一个是新欢。特征工程依赖feature_column实现，这里做的比较简单在后面的深度模型再好好搞。

问题定义

CTR本质是一个二分类问题，$X \in R^N $是用户和广告相关特征, $Y \in (0,1)$是每个广告是否被点击，基础模型就是一个简单的Logistics Regression

\[P(Y=1) = \frac{1}{1+ exp{(w_0 + \sum_{i=1}^Nw_ix_i)}}
\]

考虑在之后TF框架里logistics可以简单用activation来表示，我们把核心的部分简化为以下

\[y(x) = w_0 + \sum_{i=1}^Nw_ix_i
\]

## LR模型
2010年之前主流的CTR模型通常是最简单的logistics regression，模型可解释性强，工程上部署简单快捷。但最大的问题是依赖于大量的手工特征工程。

刚接触特征工程的同学可能会好奇为什么需要计算组合特征？

最开始我只是简单认为越细粒度的聚合特征Bias越小。接触了因果推理后，我觉得更适合用Simpson Paradox里的Confounder Bias来解释，不同聚合特征之间可能会相悖，例如各个年龄段的男性点击率均低于女性，但整体上男性的点击率高于女性。感兴趣的可以看看这篇博客因果推理的春天系列序 - 数据挖掘中的Confounding, Collidar, Mediation Bias

如果即想简化特征工程，又想加入特征组合，肯定就会想到下面的暴力特征组合方式。这个也被称作POLY2模型

\[y(x) = w_0 + \sum_{i=1}^N w_ix_i + \sum_{i=1}^N \sum_{j=i+1}^N w_{i,j} x_ix_j
\]

但上述$w_{i,j}$需要学习$\frac{n(n-1)}{2}$个参数，一方面复杂度高，另一方面对高维稀疏特征会出现大量$w_{i,j}$是0的情况，模型无法学到样本中未曾出现的特征组合pattern，模型泛化性差。

于是降低复杂度，自动选择有效特征组合，以及模型泛化这三点成为后续主要的改进的方向。

GBDT+LR模型

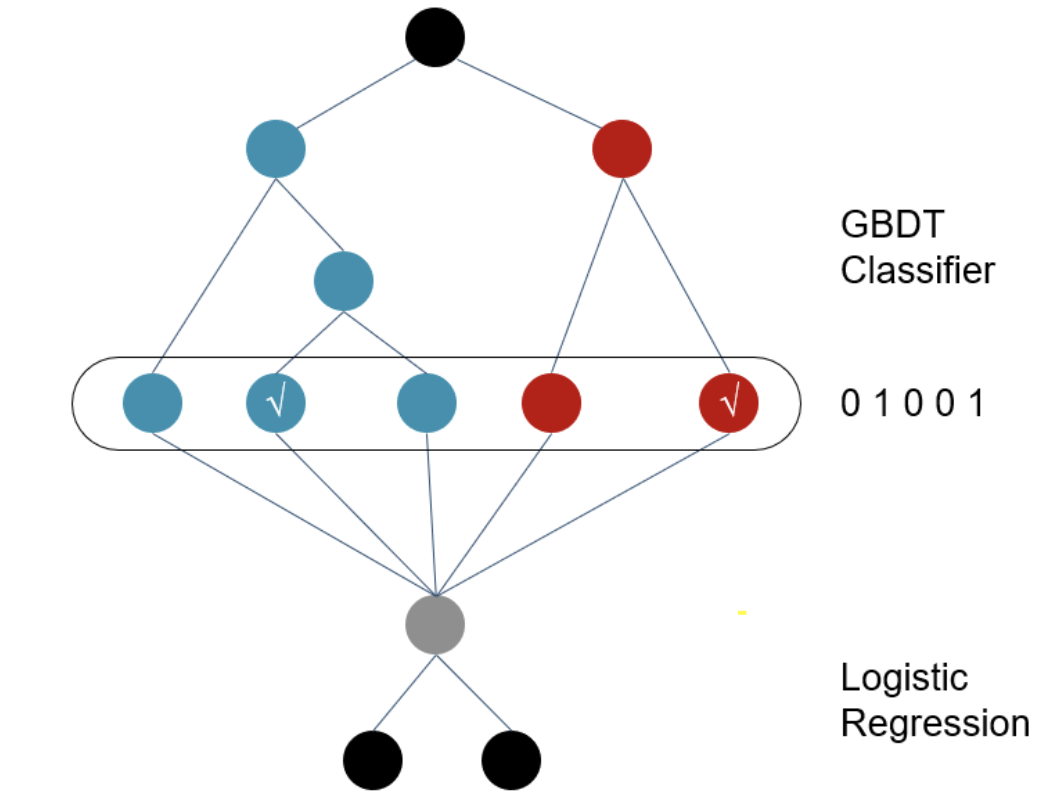
2014年Facebook提出在GBDT叠加LR的方法，敲开了特征工程模型化的大门。GBDT输出的不是预测概率，而是每一个样本落在每一颗子树哪个叶节点的一个0/1矩阵。在只保留和target相关的有效特征组合的同时，避免了手工特征组合需要的业务理解和人工成本。

相较特征组合，我更喜欢把GBDT输出的特征向量，理解为根据target，对样本进行了聚类/降维，输出的是该样本所属的几个特定人群组合，每一棵子树都对应一种类型的人群组合。

但是！GBDT依旧存在泛化问题，因为所有叶节点的选择都依赖于训练样本，并且GBDT在离散特征上效果比较有限。同时也存在经过GBDT变换得到的特征依旧是高维稀疏特征的问题。

FM模型

2010年Rendall提出的因子分解机模型(FM)为降低计算复杂度，为增加模型泛化能力提供了思路

原理

FM模型将上述暴力特征组合直接求解整个权重矩$w_ij \in R^{N*N}$，转化为求解权重矩阵的隐向量$V \in R^{N*k}$，这一步会大大增加模型泛化能力，因为权重矩阵不再完全依赖于样本中的特定特征组合，而是可以通过特征间的相关关系间接得到。同时隐向量把模型需要学习的参数数量从$\frac{n(n-1)}{2}$降低到$nk$个

\[\begin{align}
y(x) & = w_0 + \sum_{i=1}^Nw_i x_i + \sum_{i=1}^N \sum_{j=i+1}^N w_{i,j} x_ix_j\\
&= w_0 + \sum_{i=1}^Nw_i x_i + \sum_{i=1}^N \sum_{j=i+1}^N <v_i,v_j> x_ix_j\\
\end{align}
\]

同时FM通过下面的trick,把拟合过程的计算复杂度从$O(n^2k)$降低到线性复杂度$O(nk)$

\[\begin{align}
&\sum_{i=1}^N \sum_{j=i+1}^N<v_i,v_j> x_ix_j \\
= &\frac{1}{2}( \sum_{i=1}^N \sum_{j=1}^N<v_i,v_j> x_ix_j - \sum_{i=1}^N<v_i,v_i>x_ix_i)\\
= &\frac{1}{2}( \sum_{i=1}^N \sum_{j=1}^N\sum_{f=1}^K v_{if}v_{jf} x_ix_j - \sum_{i=1}^N\sum_{f=1}^Kv_{if}^2x_i^2)\\
= &\frac{1}{2}\sum_{f=1}^K( \sum_{i=1}^N \sum_{j=1}^N v_{if}v_{jf} x_ix_j - \sum_{i=1}^Nv_{if}^2x_i^2)\\
= &\frac{1}{2}\sum_{f=1}^K( (\sum_{i=1}^N v_{ij}x_i)^2 - \sum_{i=1}^Nv_{if}^2x_i^2)\\
= &\text{square_of_sum} -\text{sum_of_square}
\end{align}
\]

代码实现-自定义Keras Layer

class FM_Layer(Layer):

    """

    Input:

        factor_dim: latent vector size

        input_shape: raw feature size

        activation

    output:

        FM layer output

    """

    def __init__(self, factor_dim, activation = None, **kwargs):

        self.factor_dim = factor_dim

        self.activation = activations.get(activation) # if None return linear, else return function of identifier

        self.InputSepc = InputSpec(ndim=2) # Specifies input layer attribute. one Inspec for each input

        super(FM_Layer,self).__init__(**kwargs)

    def build(self, input_shape):

        """

        input:

            tuple of input_shape

        output:

            w: linear weight

            v: latent vector

            b: linear Bias

        func:

            define all the necessary variable here

        """

        assert len(input_shape) >=2

        input_dim = int(input_shape[-1])

        self.w = self.add_weight(name = 'w0', shape = (input_dim, 1),

                                  initializer = 'glorot_uniform',

                                  trainable = True)

        self.b = self.add_weight(name = 'bias', shape = (1, ),

                                  initializer = 'zeros',

                                  trainable = True)

        self.v = self.add_weight(name = 'hidden_vector', shape = (input_dim, self.factor_dim),

                                 initializer = 'glorot_uniform',

                                  trainable = True)

        super(FM_Layer, self).build(input_shape)# set self.built=True

    def call(self, x):

        """

        input:

            x(previous layer output)

        output:

            core calculation of the FM layer

        func:

            core calculcation of layer goes here

        """

        linear_term = K.dot(x, self.w) + self.b

        # Embedding之和，Embedding内积： (1, input_dim) * (input_dim, factor_dim) = (1, factor_dim)

        sum_square = K.pow(K.dot(x, self.v),2)

        square_sum = K.dot(K.pow(x, 2), K.pow(self.v, 2))

        # (1, factor_dim) -> (1)

        quad_term = K.mean( (sum_square - square_sum), axis=1, keepdims = True) #

        output = self.activation((linear_term+quad_term))

        return output

    def compute_output_shape(self, input_shape):

        # tf.keras回传input_shape是tf.dimension而不是tuple, 所以要cast成int

        return (int(input_shape[0]), self.output_dim)

FM和MF的关系

Factorizaton Machine 和Matrix Factorization听起来就很像，MF也确实是FM的一个特例。MF是通过对矩阵进行因子分解得到隐向量，但因为只适用于矩阵所以特征只能是二维，常见的是(user_id, item_id)组合。而同样是得到隐向量，FM将矩阵展平把离散特征都做one-hot,因此支持任意数量的输入特征。

FM和Embedding的关系

Embedding最常见于NLP中，把词的高维稀疏特征映射到低维矩阵embedding中，然后用交互函数，例如向量内积来表示词与词之间的相似度。而实际上FM计算的隐向量也是一种Embedding 的拟合方法，并且限制了只用向量内积作为交互函数。上述$X*V \in R^{K}$得到的就是Embedding向量本身。

FFM

2015年提出的FFM模型在FM的基础上加入了Field的概念

原理

上述FM学到的权重矩阵V是每个特征对应一个隐向量，两特征组合通过隐向量内积的形式来表达。FFM提出同一个特征和不同Field的特征组合应该有不同的隐向量，因此$V \in R^{N*K}$变成 $V \in R^{N*F*K}$其中F是特征所属Field的个数。以下数据中country,Data,Ad_type就是Field$(F=3)$

FM两特征交互的部分被改写为以下，因此需要学习的参数数量从nk变为nf*k。并且在拟合过程中无法使用上述trick因此复杂度从FM的$O(nk)$上升为$O(kn^2)$。

\[\begin{align}
\sum_{i=1}^N \sum_{j=i+1}^N<v_i,v_j> x_ix_j \to &\sum_{i=1}^N \sum_{j=i+1}^N<v_{i,f_j},v_{j,f_i}> x_ix_j
\end{align}
\]

代码实现-自定义model_fn

def model_fn(features, labels, mode, params):

    """

    Field_aware factorization machine for 2 classes classification

    """

    feature_columns, field_dict = build_features()

    field_dim = len(np.unique(list(field_dict.values())))

    input = tf.feature_column.input_layer(features, feature_columns)

    input_dim = input.get_shape().as_list()[-1]

    with tf.variable_scope('linear'):

        init = tf.random_normal( shape = (input_dim,2) )

        w = tf.get_variable('w', dtype = tf.float32, initializer = init, validate_shape = False)

        b = tf.get_variable('b', shape = [2], dtype= tf.float32)

        linear_term = tf.add(tf.matmul(input,w), b)

        tf.summary.histogram( 'linear_term', linear_term )

    with tf.variable_scope('field_aware_interaction'):

        init = tf.truncated_normal(shape = (input_dim, field_dim, params['factor_dim']))

        v = tf.get_variable('v', dtype = tf.float32, initializer = init, validate_shape = False)

        interaction_term = tf.constant(0, dtype =tf.float32)

        # iterate over all the combination of features

        for i in range(input_dim):

            for j in range(i+1, input_dim):

                interaction_term += tf.multiply(

                    tf.reduce_mean(tf.multiply(v[i, field_dict[j],: ], v[j, field_dict[i],:])) ,

                    tf.multiply(input[:,i], input[:,j])

                )

        interaction_term = tf.reshape(interaction_term, [-1,1])

        tf.summary.histogram('interaction_term', interaction_term)

    with tf.variable_scope('output'):

        y = tf.math.add(interaction_term, linear_term)

        tf.summary.histogram( 'output', y )

    if mode == tf.estimator.ModeKeys.PREDICT:

        predictions = {

            'predict_class': tf.argmax(tf.nn.softmax(y), axis=1),

            'prediction_prob': tf.nn.softmax(y)

        }

        return tf.estimator.EstimatorSpec(mode = tf.estimator.ModeKeys.PREDICT,

                                          predictions = predictions)

    cross_entropy = tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits( labels=labels, logits=y ))

    if mode == tf.estimator.ModeKeys.TRAIN:

        optimizer = tf.train.AdamOptimizer(learning_rate = params['learning_rate'])

        train_op = optimizer.minimize(cross_entropy,

                                     global_step = tf.train.get_global_step())

        return tf.estimator.EstimatorSpec(mode, loss = cross_entropy, train_op = train_op)

    else:

        eval_metric_ops = {

            'accuracy': tf.metrics.accuracy(labels = labels,

                                            predictions = tf.argmax(tf.nn.softmax(y), axis=1)),

            'auc': tf.metrics.auc(labels = labels ,

                                  predictions = tf.nn.softmax(y)[:,1]),

            'pr': tf.metrics.auc(labels = labels,

                                 predictions = tf.nn.softmax(y)[:,1],

                                 curve = 'PR')

        }

        return tf.estimator.EstimatorSpec(mode, loss = cross_entropy, eval_metric_ops = eval_metric_ops)

完整代码在这里 https://github.com/DSXiangLi/CTR

参考资料

S. Rendle, “Factorization machines,” in Proceedings of IEEE International Conference on Data Mining (ICDM), pp. 995–1000, 2010
Yuchin Juan，Yong Zhuang，Wei-Sheng Chin，Field-aware Factorization Machines for CTR Prediction。
盘点前深度学习时代阿里、谷歌、Facebook的CTR预估模型
前深度学习时代CTR预估模型的演化之路：从LR到FFM
推荐系统召回四模型之：全能的FM模型
主流CTR预估模型的演化及对比
深入FFM原理与实践