整数拆分-dp问题

Integer Partition

In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing nas a sum of positive integers.

Two sums that differ only in the order of their summands are considered the same partition. For example, 4 can be partitioned in five distinct ways:

4
3 + 1
2 + 2
2 + 1 + 1
1 + 1 + 1 + 1

The order-dependent composition 1 + 3 is the same partition as 3 + 1, while the two distinct compositions 1 + 2 + 1 and 1 + 1 + 2 represent the same partition 2 + 1 + 1.

input：4

output：5

思路：

1.不考虑新加入的数，达到总和N的的种数n1

2.考虑新加入的数，达到总和N的的种数n2

3.output=n1+n2

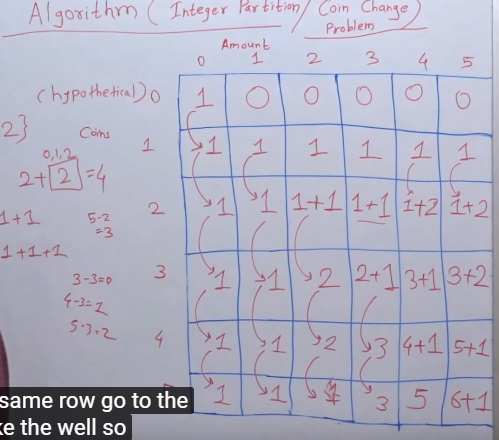
代码：

/**
 * @param {number} number
 * @return {number}
 */
export default function integerPartition(number) {
  // Create partition matrix for solving this task using Dynamic Programming.
  const partitionMatrix = Array(number + ).fill(null).map(() => {
    return Array(number + ).fill(null);
  });
  for (let numberIndex = ; numberIndex <= number; numberIndex += ) {
    partitionMatrix[][numberIndex] = ;
  }
  for (let summandIndex = ; summandIndex <= number; summandIndex += ) {
    partitionMatrix[summandIndex][] = ;
  }

  // Now let's go through other possible options of how we could form number m out of
  // summands 0, 1, ..., m using Dynamic Programming approach.
  for (let summandIndex = ; summandIndex <= number; summandIndex += ) {//行-被加数
    for (let numberIndex = ; numberIndex <= number; numberIndex += ) {//input代表的列
      if (summandIndex > numberIndex) {
        // If summand number is bigger then current number itself then just it won't add
        // any new ways of forming the number. Thus we may just copy the number from row above.
        partitionMatrix[summandIndex][numberIndex] = partitionMatrix[summandIndex - ][numberIndex];
      } else {
        /*
         * The number of combinations would equal to number of combinations of forming the same
         * number but WITHOUT current summand number PLUS number of combinations of forming the
         * <current number - current summand> number but WITH current summand.
         *
         * Example:
         * Number of ways to form 5 using summands {0, 1, 2} would equal the SUM of:
         * - number of ways to form 5 using summands {0, 1} (we've excluded summand 2)
         * - number of ways to form 3 (because 5 - 2 = 3) using summands {0, 1, 2}
         * (we've included summand 2)
        */
        const combosWithoutSummand = partitionMatrix[summandIndex - ][numberIndex];
        const combosWithSummand = partitionMatrix[summandIndex][numberIndex - summandIndex];

        partitionMatrix[summandIndex][numberIndex] = combosWithoutSummand + combosWithSummand;
      }
    }
  }

  return partitionMatrix[number][number];
}