【机器学习实战学习笔记(1-2)】k-近邻算法应用实例python代码

文章目录

• 1.改进约会网站匹配效果
• 1.1 准备数据：从文本文件中解析数据
• 1.2 分析数据：使用Matplotlib创建散点图
• 1.3 准备数据：归一化特征
• 1.4 测试算法：作为完整程序验证分类器
• 1.5 使用算法：构建完成可用系统
• 2.手写识别系统
• 2.1 准备数据：将图像转换为测试向量
• 2.2 测试算法：使用k-近邻算法识别手写数字

在上一篇文章中我们得到了基于欧式距离、多数表决规则，实现方法采用线性搜索法的k-近邻法classify0(inX, dataSet, labels, k)，现在用这个函数来做一些应用k-近邻法的分类应用实例。

1.改进约会网站匹配效果

训练样本数据集为约会样本数据，即datingTestSet2.txt。文件中每个样本数据占据一行，共有1000行。

数据集的部分示例如下图所示：



该样本分别包括以下三种特征：

• 每年获得的飞行常客里程数
• 玩视频游戏所耗时间百分比
• 每周消费的冰淇淋公升数

样本标签有三类：

• 不喜欢的人(1)
• 魅力一般的人(2)
• 极具魅力的人(3)

1.1 准备数据：从文本文件中解析数据

## 将文本记录解析为classify0中需要的dataSet, labels的形式
def file2matrix(filename):
    # 得到文件行数
    with open(filename) as f:
        arrayOLines = f.readlines()
    numberOfLines = len(arrayOLines)
    # 创建返回的NumPy矩阵(dataSet, labels)
    returnMat = zeros((numberOfLines,3))
    classLabelVetor = []
    index = 0
    # 解析文件数据到列表
    for line in arrayOLines:
        line = line.strip()
        listFromLine = line.split('\t')
        returnMat[index,:] = listFromLine[0:3]
        classLabelVetor.append(int(listFromLine[-1]))
        index += 1
    return returnMat,classLabelVetor

1.2 分析数据：使用Matplotlib创建散点图

import matplotlib.pyplot as plt

datingDataMat,datingLabels = file2matrix('datingTestSet2.txt')

plt.rcParams['font.sans-serif'] = ['SimHei']
fig = plt.figure(figsize=(12,10))
ax = fig.add_subplot(221)
ax.set_xlabel("玩视频游戏所耗时间百分比")
ax.set_ylabel("每周消费的冰淇淋公升数")
ax.scatter(datingDataMat[:,1], datingDataMat[:,2], s=15.0*array(datingLabels), c=15.0*array(datingLabels))#根据样本类别，绘制不同颜色，不同大小的散点

ax1 = fig.add_subplot(222)
ax1.set_xlabel("每年获取的飞行常客里程数")
ax1.set_ylabel("每周消费的冰淇淋公升数")
ax1.scatter(datingDataMat[:,0], datingDataMat[:,2], s=15.0*array(datingLabels), c=15.0*array(datingLabels))

ax2 = fig.add_subplot(212)
ax2.set_xlabel("每年获取的飞行常客里程数")
ax2.set_ylabel("玩视频游戏所耗时间百分比")
ax2.scatter(datingDataMat[:,0], datingDataMat[:,1], s=15.0*array(datingLabels), c=15.0*array(datingLabels))

plt.show()

绘制出的散点图如下所示：



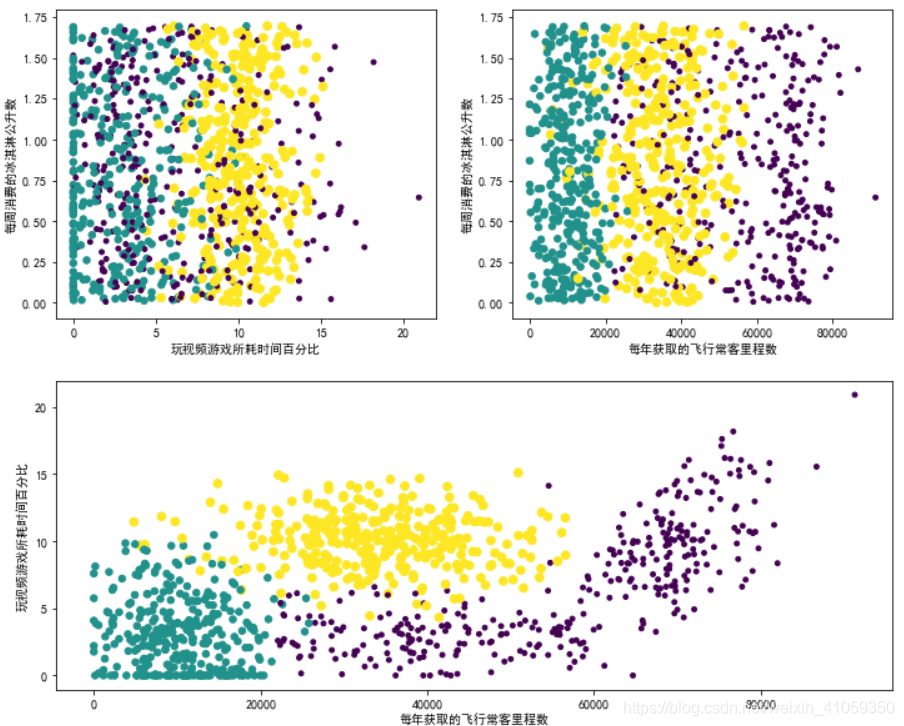
从上述图片可以看出，datingDataMat矩阵第一列和第二列属性，即“玩视频游戏所耗时间百分比”、“每年获取的飞行常客里程数”，得到了较好的展示效果，图中清晰地表示了三个不同的样本分类区域，即这两个特征更容易区分数据点从属的类别。

1.3 准备数据：归一化特征

先来计算训练样本中两条样本之间的距离：

(20000−32000)2+(0−67)2+(1.1−0.1)2\sqrt{(20000-32000)^2+(0-67)^2+(1.1-0.1)^2}(20000−32000)2+(0−67)2+(1.1−0.1)2​

很容易看出，上面方程中数字差值最大的属性对计算结果的影响最大，也就是说“每年获取的飞行常客里程数”对于计算结果的影响远远大于其他两个特征，但是实际上这三种特征是同等重要的，即三个等权重特征。

因此应进行特征归一化，将各特征归一化到一个类似的取值范围内，如[0,1]或者[-1,1]。这里我们选择将特征归一化到[0,1]：

newValue=(oldValue−min)(max−min)newValue = \frac{(oldValue-min)}{(max-min)}newValue=(max−min)(oldValue−min)​

# 归一化特征值
def autoNorm(dataSet):
    minVals = dataSet.min(0) # 从列中选取最小值
    maxVals = dataSet.max(0)
    ranges = maxVals - minVals
    normDataSet = zeros(shape(dataSet))
    m = dataSet.shape[0]
    normDataSet = dataSet - tile(minVals, (m,1))
    normDataSet = normDataSet/tile(ranges, (m,1)) # 矩阵对应位置相除，矩阵除法用linalg.solve(matA,matB)
    return normDataSet, ranges, minVals

1.4 测试算法：作为完整程序验证分类器

这里用训练数据集10% 的数据来做测试。

需要说明的一点：10%的测试数据应该是随机选择的，由于这里用到的数据并没有按照特定目的排序，也没有规律，所以我们可以随意选择10%数据而不影响其随机性。

# 分类器针对约会网站的测试代码
def datingClassTest():
    hoRation = 0.10
    datingDataMat,datingLabels = file2matrix('/datingTestSet2.txt')
    normMat, ranges, minVals = autoNorm(datingDataMat)
    m = normMat.shape[0]
    numTestVecs = int(m*hoRation)
    errorCount = 0.0
    for i in range(numTestVecs):
        classifierResult = classify0(normMat[i,:], normMat[numTestVecs:m,:], datingLabels[numTestVecs:m], 3)
        #print("the classifier came back with: %d, the real answer is: %d" %(classifierResult,datingLabels[i]))
        if (classifierResult != datingLabels[i]): errorCount += 1.0
    print("the total error rate is: %f" %(errorCount/float(numTestVecs)))

输出：

the total error rate is: 0.050000，分类器处理约会数据集的错误率为5%，还不错。

1.5 使用算法：构建完成可用系统

# 约会网站测试函数
def classifyPerson():
    resultList = ['not at all', 'in small doses', 'in large doses']
    percentTats = float(input("percentage of time spent playing video games?"))
    ffMiles = float(input("frequent flier miles earned per year?"))
    iceCream = float(input("liters of ice cream consumed per year?"))
    datingDataMat, datingLabels = file2matrix('datingTestSet2.txt')
    normMat, ranges, minVals = autoNorm(datingDataMat)
    inArr = array([ffMiles, percentTats, iceCream])
    classifierResult = classify0((inArr-minVals)/ranges,normMat,datingLabels,3)
    print("You will probably like this person:",resultList[classifierResult - 1])

2.手写识别系统

训练样本数据集部分示例如下所示：

文件名0_1表示该文件是第1个0的表示，32*32

2.1 准备数据：将图像转换为测试向量

# 将32*32的二进制图像转为1*1024的向量
def img2vector(filename):
    returnVect = zeros((1,1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVect[0, 32*i+j] = int(lineStr[j])
    fr.close()
    return returnVect

2.2 测试算法：使用k-近邻算法识别手写数字

from os import listdir
#listdir 列出给定目录的文件名

# 手写数字识别系统测试
def handwritingClassTest():
    hwLabels = []
    trainingFileList = listdir('trainingDigits')
    m = len(trainingFileList)
    trainingMat = zeros((m,1024))
    for i in range(m):
        fileNameStr = trainingFileList[i]
        fileStr = fileNameStr.split('.')[0]
        classNumStr = int(fileStr.split('_')[0])
        hwLabels.append(classNumStr)
        trainingMat[i,:] = img2vector('trainingDigits/%s' % fileNameStr)
    testFileList = listdir('testDigits')
    errorCount = 0.0
    mTest = len(testFileList)
    for i in range(mTest):
        fileNameStr = testFileList[i]
        fileStr = fileNameStr.split('.')[0]
        classNumStr = int(fileStr.split('_')[0])
        vectorUnderTest = img2vector('testDigits/%s' % fileNameStr)
        classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3)
        #print("the classifier came back with %d, the real answer is %d" % (classifierResult, classNumStr))
        if (classifierResult != classNumStr): errorCount += 1.0
    print('\n the total number of errors is: %d' % errorCount)
    print('\n the total error rate is: %f' % (errorCount/float(mTest)))

输出：

the total number of errors is: 10

the total error rate is: 0.010571

在运行这个手写数字识别系统测试函数的时候可以明显感觉到我们前面说的，基于线性搜索法的k-近邻法执行效率并不高，抽时间学一下k决策树的实现再来补上代码。