推荐系统之矩阵分解（MF）

一、矩阵分解

1.案例

我们都熟知在一些软件中常常有评分系统，但并不是所有的用户user人都会对项目item进行评分，因此评分系统所收集到的用户评分信息必然是不完整的矩阵。那如何跟据这个不完整矩阵中已有的评分来预测未知评分呢。使用矩阵分解的思想很好地解决了这一问题。

假如我们现在有一个用户-项目的评分矩阵R（n，m）是n行m列的矩阵，n表示user个数，m行表示item的个数



那么，如何根据目前的矩阵R（5,4）如何对未打分的商品进行评分的预测（如何得到分值为0的用户的打分值）？

——矩阵分解的思想可以解决这个问题，其实这种思想可以看作是有监督的机器学习问题（回归问题）。

矩阵分解的过程中，,矩阵R可以近似表示为矩阵P与矩阵Q的乘积：

矩阵P(n,k)表示n个user和k个特征之间的关系矩阵，这k个特征是一个中间变量，矩阵Q(k,m)的转置是矩阵Q(m,k)，矩阵Q(m,k)表示m个item和K个特征之间的关系矩阵，这里的k值是自己控制的，可以使用交叉验证的方法获得最佳的k值。为了得到近似的R(n,m)，必须求出矩阵P和Q，如何求它们呢？

2.推导步骤

1.首先令：

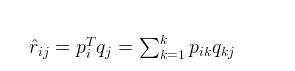
2。对于式子1的左边项，表示的是r^ 第i行，第j列的元素值，对于如何衡量，我们分解的好坏呢，式子2，给出了衡量标准，也就是损失函数，平方项损失，最后的目标，就是每一个元素(非缺失值)的e(i,j)的总和最小值

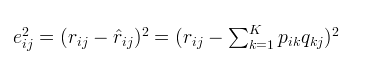
3.使用梯度下降法获得修正的p和q分量：

• 求解损失函数的负梯度

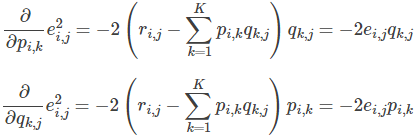
• 根据负梯度的方向更新变量：

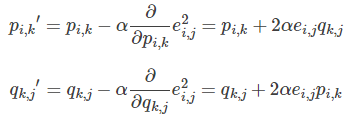
4.不停迭代直到算法最终收敛（直到sum(e^2) <=阈值，即梯度下降结束条件：f(x)的真实值和预测值小于自己设定的阈值）

5.为了防止过拟合，增加正则化项

3.加入正则项的损失函数求解

1.通常在求解的过程中，为了能够有较好的泛化能力，会在损失函数中加入正则项，以对参数进行约束，加入正则L2范数的损失函数为：

对正则化不清楚的，公式可化为：

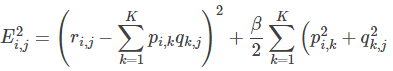
2.使用梯度下降法获得修正的p和q分量：

• 求解损失函数的负梯度：

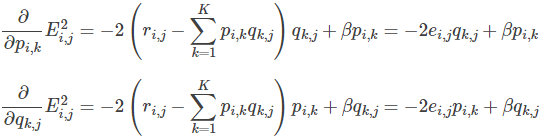
• 根据负梯度的方向更新变量：

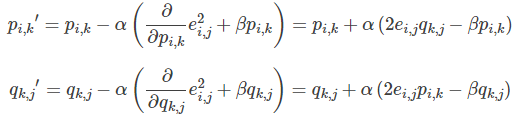
4.预测

预测利用上述的过程，我们可以得到矩阵和，这样便可以为用户 i 对商品 j 进行打分：

二、代码实现

import numpy as np
import matplotlib.pyplot as plt

def matrix(R, P, Q, K, alpha, beta):
    result=[]
    steps = 1
    while 1 :
    #使用梯度下降的一步步的更新P,Q矩阵直至得到最终收敛值
        steps = steps + 1
        eR = np.dot(P,Q)
        e=0
        for i in range(len(R)):
            for j in range(len(R[i])):
                if R[i][j]>0:
                    # .dot(P,Q) 表示矩阵内积,即Pik和Qkj k由1到k的和eij为真实值和预测值的之间的误差,
                    eij=R[i][j]-np.dot(P[i,:],Q[:,j])
                    #求误差函数值，我们在下面更新p和q矩阵的时候我们使用的是化简得到的最简式，较为简便，
                    #但下面我们仍久求误差函数值这里e求的是每次迭代的误差函数值，用于绘制误差函数变化图
                    e=e+pow(R[i][j] - np.dot(P[i,:],Q[:,j]),2)
                    for k in range(K):
                        #在上面的误差函数中加入正则化项防止过拟合
                        e=e+(beta/2)*(pow(P[i][k],2)+pow(Q[k][j],2))

                    for k in range(K):
                        #在更新p,q时我们使用化简得到了最简公式
                        P[i][k]=P[i][k]+alpha*(2*eij*Q[k][j]-beta*P[i][k])
                        Q[k][j]=Q[k][j]+alpha*(2*eij*P[i][k]-beta*Q[k][j])
        print('迭代轮次:', steps, '   e:', e)
        result.append(e)#将每一轮更新的损失函数值添加到数组result末尾

        #当损失函数小于一定值时，迭代结束
        if eij<0.00001:
            break
    return P,Q,result

R=[
   [5,3,1,1,4],
   [4,0,0,1,4],
   [1,0,0,5,5],
   [1,3,0,5,0],
   [0,1,5,4,1],
   [1,2,3,5,4]
   ]

R=np.array(R)

alpha = 0.0001 #学习率
beta = 0.002 

N = len(R) #表示行数
M = len(R[0]) #表示列数
K = 3 #3个因子

p = np.random.rand(N, K) #随机生成一个 N行 K列的矩阵
q = np.random.rand(K, M) #随机生成一个 M行 K列的矩阵

P, Q, result=matrix(R, p, q, K,  alpha, beta)
print("矩阵Q为：\n",Q)
print("矩阵P为：\n",P)
print("矩阵R为：\n",R)
MF = np.dot(P,Q)
print("预测矩阵：\n",MF)

#下面代码可以绘制损失函数的收敛曲线图
n=len(result)
x=range(n)
plt.plot(x, result,color='b',linewidth=3)
plt.xlabel("generation")
plt.ylabel("loss")
plt.show()