自己实现一个 DFA 串模式识别器

前言

这是我编译原理课程的实验。希望读完这篇文章的人即便不知道 NFA，DFA 和正规表达式是什么，也能够对它们有一个简单的理解，并能自己去实现一个能够识别特定模式的串模式识别器。它可能会像是这样：

输入一个正规表达式：(s.f.l*.e)|(a*.b*)

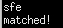
输入：“sfe”

输出：matched！

输入：“sflea”

输出：failed！

注：'.' （点字符）表示连接运算

文章分为两部分，理论背景：介绍相关概念和原理；程序实现：使用 C++ 实现一个 DFA 串模式识别器。

理论背景

引入

我比较喜欢将任何理论和技术从自己能应用和理解的最低点开始阐述，因为这样往往可以将新的知识与过往的知识体系相联结。同时在一定的场景下思考它如何被应用，以切实的实现将所学流畅的抵达所用。这篇文章亦是如此。

首先我们要处理一个简单的问题，给出如下串：

例一：

ab,abab,ababab,abababab,...

a,aa,aaa,aaaa,...

aab,aabaab,aabaabaab,...

对于第一行给出的这些字符串，请问你是否能够编写简单程序，识别出给定的一个字符串 S 是否属于第一行中的某一个字符串？如 ab 属于第一行，abab 属于第一行，但 aab 不属于。我相信有过一定编程经验的人都可以通过简单的分支-循环逻辑，或者是一些字符串算法来写出一个判别程序。对于第二、三行也是如此。因为我们发现它们都具有一定的规律性,或者也可以称为遵循一定的模式。当情况很简单时我们并不用思考太多，只是不断的复杂化、堆叠我们的逻辑代码，希望代码逻辑能够捕获特定模式下所有的串。不过有时情况会很复杂，以至于我们非常困难去设计一个逻辑来实现判别（捕获模式）。比如下面这个串：

例二：

abb,aabb,babb,ababb,aaaaaaabb,bbbbbbbbabb,aababbababbbabbabb,

ababababaaaaaaabbbbbbbaaaaaaabbbbbaababbbabababbabbbbaabb,...

你可能会觉得这些串完全没有任何逻辑和规律可言嘛！没错，单凭对已给出的这些串很难发现规律。但是它确实有自己的模式，而且我可以提前告诉你，它们是由我根据正则（规）表达式：(a|b)*abb 产生的。如果你没有了解过正则（规）表达式也不必担心,先跳过它。

注：在某些不严格情况下，不区分正规表达式和正则表达式

模式串和正规表达式

在前文中，我重复了很多次模式这个词。其实我们之前看到的每一组串都是遵循特定的模式。非正式的，我们可以说一组字符串构成的集合由一个与该组相关的称为模式的规则来描述。并且这个模式被说成匹配该集合中的每个字符串。

注：这里的模式特指串的模式

可以以例一为例介绍模式。非正式的表示：

例一的第一行的模式为：由 a、b 交替出现组成的串

第二行模式为：由若干个 a 组成的串

第三行模式为：由若干个 abb 组成的串

我们可以用自然语言描述简单的模式，但是无法去描述复杂的模式。所以就需要一种形式化的表示方法，来帮助我们表达。这就是正规表达式。正规表达式是表示模式的一种重要方法。每个模式匹配一个字符串集。简单来说，正规表达式需要一个字母表，其中字母表上的字符串是该字母表中符号的有穷序列。和定义在其上的一些运算。通过归纳已有的模式串，我们可以提出以下几种运算：

连接运算：以英文 '.' 表示。如：a.b 表示串 ab

或运算：以英文 '|' 表示。如：a|b 表示串 a 或串 b

克林闭包运算：以英文 '*' 表示。如：a* 表示串：$\epsilon$ ，a，aa，aaa，...

注：1. $\epsilon$ 表示空串 2. 为了我的程序方便处理，我将连接运算设置成了英文的点。

需要注意的是，运算并不止上述三种，但是我们主要讨论他们，并且很多运算可以通过它们复合得到。如：

正闭包：以英文：'+' 表示，当字母表只有 a 时 a+ 等价于 a.a*

? 运算：以英文：'?' 表示，当字母表只有 a 时 a? 等价于 (a|$\epsilon$)

指数运算等

现在我们将例二中的正规表达式重新书写为：(a|b)*a.b.b 。参照上述运算的含义，我想你应该可以理解这个模式所代表的串的集合会是什么样的。

注意，正规表达式所能描述的模式是有限的。它只能表示固定次数的重复或给定结构没有指定次数的重复。它不能用于描述均衡或者嵌套结构。如具有括号配对的符号串集合正规文法无法描述，但是可以通过更复杂的上下文无关文法来描述。关于文法不作多描述。

出于篇幅考虑和更好的阅读体验，本文将分成三个部分，欢迎继续阅读余下篇章。下一篇内容是正规表达式的实现原理，涉及 NFA、DFA 的概念和相关算法。

作者：Skipper

出处：https://www.cnblogs.com/backwords/p/12726258.html

本博客中未标明转载的文章归作者 Skipper 和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。