2019ICPC南京网络赛A题 The beautiful values of the palace(三维偏序)

2019ICPC南京网络赛A题

The beautiful values of the palace

https://nanti.jisuanke.com/t/41298

Here is a square matrix of n * nn∗n, each lattice has its value (nn must be odd), and the center value is n * nn∗n. Its spiral decline along the center of the square matrix (the way of spiral decline is shown in the following figure:)

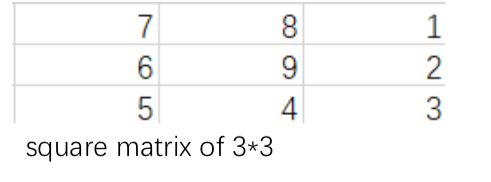
The grid in the lower left corner is (1,1) and the grid in the upper right corner is (n , n)

Now I can choose mm squares to build palaces, The beauty of each palace is equal to the digital sum of the value of the land which it is located. Such as (the land value is 123213123213,the beautiful values of the palace located on it is 1+2+3+2+1+3=121+2+3+2+1+3=12) (666666 -> 1818) (456456 ->1515)

Next, we ask pp times to the sum of the beautiful values of the palace in the matrix where the lower left grid(x_1,y_1x1,y1), the upper right square (x_2,y_2x2,y2).

Input

The first line has only one number TT.Representing TT-group of test data (T\le 5)(T≤5)

The next line is three number: n \ m \ pn m p

The mm lines follow, each line contains two integers the square of the palace (x, y )(x,y)

The pp lines follow, each line contains four integers : the lower left grid (x_1,y_1)(x1,y1) the upper right square (x_2,y_2)(x2,y2)

Output

Next, p_1+p_2...+p_Tp1+p2...+p**T lines: Represent the answer in turn(n \le 10^6)(m , p \le 10^5)(n≤106)(m,p≤105)

样例输入复制

1
3 4 4
1 1
2 2
3 3
2 3
1 1 1 1
2 2 3 3
1 1 3 3
1 2 2 3

样例输出复制

5
18
23
17

思路：

三维偏序的题目

首先根据推公式可以把每一个点在螺旋矩阵中对应的数值求出。

然后我们把m个点当做成m个加点操作，

p个询问，每一个询问分解为4个子询问，对同一个答案计算贡献。

因为根据容斥原理，我们可以把求二维前缀和分解为4个以左下角点为（0，0）的4个前缀和来处理。，

然后对x，y进行排序，

坐标相同时，一定要加点的操作排在询问前面。

然后用树桩数组来维护偏序问题即可。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
#define du3(a,b,c) scanf("%d %d %d",&(a),&(b),&(c))
#define du2(a,b) scanf("%d %d",&(a),&(b))
#define du1(a) scanf("%d",&(a));
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) {a %= MOD; if (a == 0ll) {return 0ll;} ll ans = 1; while (b) {if (b & 1) {ans = ans * a % MOD;} a = a * a % MOD; b >>= 1;} return ans;}
void Pv(const vector<int> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%d", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
void Pvl(const vector<ll> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%lld", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}

inline void getInt(int *p);
const int maxn = 1000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/

ll tree[maxn];
int lowbit(int x)
{
    return -x & x;
}
ll ask(int x)
{
    ll res = 0ll;
    while (x) {
        res += tree[x];
        x -= lowbit(x);
    }
    return res;
}
void add(int x, ll val)
{
    while (x < maxn) {
        tree[x] += val;
        x += lowbit(x);
    }
}
ll re_val(ll x)
{
    ll sum = 0;
    while (x > 0) {
        sum += x % 10;
        x /= 10;
    }
    return sum;
}
long long index(long long y, long long x, long long n)
{
    long long mid = (n + 1) / 2;
    long long p = max(abs(x - mid), abs(y - mid));
    long long ans = n * n - (1 + p) * p * 4;
    long long sx = mid + p, sy = mid + p;
    if (x == sx && y == sy) {
        return ans;
    } else {
        if (y == sy || x == sx - 2 * p) {
            return ans + abs(x - sx) + abs(y - sy);
        } else {
            return ans + 8 * p - abs(x - sx) - abs(y - sy);
        }
    }
}
int tot;
struct node {
    int type;
    int id;
    ll k;
    ll x, y;
    ll val;
    node() {}
    node(int tt, int idd, ll kk, ll xx, ll yy, ll vv)
    {
        id = idd;
        type = tt;
        k = kk;
        x = xx;
        y = yy;
        val = vv;
    }
} a[maxn];
bool cmp(node aa, node bb)
{
    if (aa.y != bb.y) {
        return aa.y < bb.y;
    } else if (aa.x != bb.x) {
        return aa.x < bb.x;
    } else {
        return aa.type < bb.type;
    }
}
ll ans[maxn];
void solve()
{
    repd(i, 1, tot) {
        if (a[i].type) {
            ans[a[i].id] += a[i].k * ask(a[i].x);
        } else {
            add(a[i].x, a[i].val);
        }
    }
}
int main()
{
    //freopen("D:\\code\\text\\input.txt","r",stdin);
    //freopen("D:\\code\\text\\output.txt","w",stdout);
    int t;
    du1(t);
    while (t--) {
        int n, m, p;
        du3(n, m, p);
        MS0(tree);
        tot = 0;
        repd(i, 1, m) {
            int x, y;
            du2(x, y);
            ll val = re_val(index(x, y, n));
            a[++tot] = node(0, 0, 1ll, x, y , val);
        }
        repd(i, 1, p) {
            ans[i] = 0ll;
            int lx, ly, rx, ry;
            du3(lx, ly, rx); du1(ry);
            a[++tot] = node(1, i, 1ll, rx, ry , 0);
            a[++tot] = node(1, i, 1ll, lx - 1, ly - 1 , 0);
            a[++tot] = node(1, i, -1ll, rx, ly - 1 , 0);
            a[++tot] = node(1, i, -1ll, lx - 1, ry , 0);
        }
        sort(a + 1, a + 1 + tot, cmp);
        solve();
        repd(i, 1, p) {
            printf("%lld\n", ans[i] );
        }
    }
    return 0;
}

inline void getInt(int *p)
{
    char ch;
    do {
        ch = getchar();
    } while (ch == ' ' || ch == '\n');
    if (ch == '-') {
        *p = -(getchar() - '0');
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 - ch + '0';
        }
    } else {
        *p = ch - '0';
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 + ch - '0';
        }
    }
}