最小生成树之Prim Kruskal算法（转）

最小生成树

首先，生成树是建立在无向图中的，对于有向图，则没有生成树的概念，所以接下来讨论的图均默认为无向图。对于一个有n个点的图，最少需要n-1条边使得这n个点联通，由这n-1条边组成的子图则称为原图的生成树。一般来说，一个图的生成树并不是唯一的（除非原图本身就是一棵树）。

现在考虑带权图G，即图的边带权，则最小生成树就是在G中权值和最小的一颗生成树，显然最小生成树也不是唯一的，但是其权值唯一。有很多应用需要用到最小生成树的概念，比较直观的一个应用就是：有n个村庄，现在要在这些村庄之间修一些路，其中村庄i和村庄j之间的距离是Dij，现在要修最短的路使得所有村庄连接起来。

显然，这个问题可以直接套用最小生成树模型，找出最小生成树即找到了一个方案。

下面举一个最小生成树的例子：

对于如何寻找一个带权图的最小生成树，已经有了专门的求解方法，在具体讲解这些算法之前，我们这里先来挖掘一下最小生成树的一些特性，即一颗生成树要成为最小生成树，需要满足什么条件。

MST性质：

设一个带权无向图G（V,E,W）（V代表点集，E代表边集，W代表权值集），且T为Ｇ的一颗生成树，对于Ｅ中任意一条不属于Ｔ的边ｅ，将其加入Ｔ中，会产生一条环（否则T不连通），如果e始终是环中权值最大的一条边，那么说明T满足MST性质。

以上是MST性质的定义，其中MST就是最小生成树的意思，但是现在并没有证明这个性质和最小生成树有什么关系，接下来将要证明，一颗生成树是最小生成树，当且仅当它满足MST性质。

引理1：对于图Ｇ（V,E,W）的两颗生成树T1和T2，若它们都满足MST性质，则它们的权值和相同。

证明：运用数学归纳法证明当有k条边在T1中而不在T2中时（0<=k<=n-1，同样的，这是也有k条边在T2中而不在T1中），T1的权值和等于T2的权值和。

1：首先，当k=0时，说明T1和T2的所有边都一样，则T1和T2是同一颗生成树，显然它们的权值和相等。

2：现在设当k<x时，T1和T2的权值和相等，现在要证明当k=x时，T1，T2权值和依然相等。考虑这样的边集S，它们在T1或T2中，但是不同时存在于T1和T2。在S中，取权值最小的那条边，设为e（u，v），不妨认为它在T1中（在T2中同理）。e连接了图中u，v两点。考虑T2中u到v之间的路径，设为E1,E2......Em(m>1)，其中一定存在若干条边不在T1中（否则T1中存在环），设e'为这些边中的一条。

（1）e’和e都属于S，所以e'的权值不小于e。

（2）由于T2满足MST性质，且e不属于T2，那么可知e'的权值不大于e。

综上所述，e的权值和e'的权值相等，所以，将T2的边e'去掉，换成e，变成T2'，显然，T2'和T2的权值和相等，又T2'与T1只有x-1条边不同（即有x-1条边在T1中而不在T2中）。由归纳法可知T2'和T1的权值和相等，所以T2和T1的权值和相等。

证毕。

有了引理1，那么MST性质和最小生成树的关系就很容易证明了。

定理1：一颗生成树T是最小生成树，当且仅当它满足MST性质。

证明：

1：最小生成树->满足MST性质

设Ｔ是Ｇ（V,E,W）的最小生成树，采用反证法，如果T不满足MST性质，那么说明存在一条边e，其不存在与T中，将其加入T中后，它不是环中权值最大的边，设环中比e还大的边为e',那么我们将T中的e'去掉，换成e,得到的生成树T'将会拥有更小的权值和，这和T是最小生成树矛盾，所以，如果T是最小生成树，则Ｔ一定满足ＭＳＴ性质。

２：满足MST性质->最小生成树

设T是G(V,E,W)的生成树，其满足MST性质。由1我们知道，G的最小生成树满足MST性质，再由引理1，我们知道，两颗满足MST性质的生成树权值和相等，所以T的权值和与最小生成树相等，所以Ｔ是Ｇ的一颗最小生成树。

证毕。

以上证明了最小生成树的一个关键性质，下面是时候讲解求解最小生成树的具体算法了。求解最小生成树有两个经典算法。Prim算法和Kruskal算法。下面分别介绍这两个算法的步骤和正确性证明。

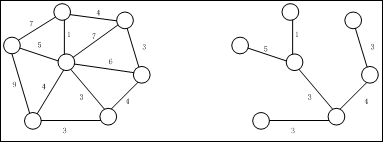
Prim算法:

Prim算法基于一种贪心的思想，通过局部最优策略，每次将一条边加入所构建的生成树中，加完n-1条边后，保证最后所得的生成树是整体最优的，即最小生成树。下面简单说明下Prim算法的步骤：

Prim算法将图中的每个点分成三种状态：

第一种tree点，表示该点已经在所构造的生成树中。

第二种fringe点，表示还没在树中，但是和Tree点相邻（有一条边直接相连），是即将要加入生成树中的候选点。

第三种unseen点，其他的点，表示还没有检测到的点。

那么Prim算法步骤为：

1：初始时将所有点初始化成unseen，并且随机将一个点S设为tree点（如1号点）。

2：将所有与S相邻的点设为fringe。

3：如果图中还存在fringe点，则到4，否则到6。

4：在所有连接一个fringe点和一个tree点的边中，取权值最小的边e（u，v），不妨设u为tree点，v为fringe点，将v点设为tree点。

5：将所有与v相邻的unseen点设为fringe，并将e加入到构建的生成树中。转到3。

6 : 如果图中所有点均为tree点，则图的一个最小生成树找到。否则原图不存在最小生成树。

7：算法结束。

根据所给算法描述，很容易得到算法的代码实现，算法实现需要用到堆优化，不熟悉堆的朋友可以自行上网查询，这里不再赘述：

//Prim
struct edge{
int to,len,next;
}e[maxm];
int box[maxn],cnt,used[maxn];
void init(int n){
for(int i=0;i<=n;i++)box[i]=-1;
cnt=0;
}
void add(int from,int to,int len){
e[cnt].to=to;
e[cnt].len=len;
e[cnt].next=box[from];
box[from]=cnt++;
}
struct node{
int v,len;
node(){}
node(int x,int y):v(x),len(y){}
bool operator<(const node &x)const{
return len>x.len;
}
};
priority_queue<node> pq;
int Prim(int n,int m){
memset(used,0,sizeof(used));//初始化所有点，设状态为unseen
int num=0,sum=0,now=1;
do{
used[now]=1;
for(int t=box[now];t+1;t=e[t].next){
int v=e[t].to,len=e[t].len;
if(!used[v])pq.push(node(v,len));
}
while(!pq.empty()){
node tmp=pq.top();pq.pop();
int v=tmp.v,len=tmp.len;
if(used[v])continue;
now=v;
sum+=len;
break;
}
num++;
}while(num<n);
return sum;
}

//Prim

struct edge{

    int to,len,next;

}e[maxm];

int box[maxn],cnt,used[maxn];

void init(int n){

    for(int i=0;i<=n;i++)box[i]=-1;

    cnt=0;

}

void add(int from,int to,int len){

    e[cnt].to=to;

    e[cnt].len=len;

    e[cnt].next=box[from];

    box[from]=cnt++;

}

struct node{

    int v,len;

    node(){}

    node(int x,int y):v(x),len(y){}

    bool operator<(const node &x)const{

        return len>x.len;

    }

};

priority_queue<node> pq;

int Prim(int n,int m){

    memset(used,0,sizeof(used));//初始化所有点，设状态为unseen

    int num=0,sum=0,now=1;

    do{

        used[now]=1;

        for(int t=box[now];t+1;t=e[t].next){

            int v=e[t].to,len=e[t].len;

            if(!used[v])pq.push(node(v,len));

        }

        while(!pq.empty()){

            node tmp=pq.top();pq.pop();

            int v=tmp.v,len=tmp.len;

            if(used[v])continue;

            now=v;

            sum+=len;

            break;

        }

        num++;

    }while(num<n);

    return sum;

}

现在来看看为什么Prim算法是正确的。

首先，如果一个图存在最小生成树，那么由上面的算法得到的一定是一颗生成树。因为当算法结束时，所有的点均为tree点，说明所有点都连通。并且得到的子图不会存在环，因为我们增加一条边时，这条边连接的一定是一个tree点和一个finge点，只有连接两个tree点时才会产生环。

前面的定理1告诉我们，一颗生成树是最小生成树，那么当且仅当它满足MST性质，那么我们只要证明Prim算法得到的生成树满足MST性质即可。

定理2：设带全图G(V,E,W)存在最小生成树，那么Prim算法得到的生成树就是G的最小生成树。

证明：我们只要证明，Prim算法得到的生成树满足MST性质即可，这可由归纳法证明。下面证明，当加入第k个点时（1<=k<=n），Prim算法得到生成树满足MST性质：

1：当k=1时，只有一个点，显然满足MST性质。

2：当k>1时，我们假设当1k<x时，均满足，当k=x时，假设当前所加入的边为e(u,v),同样地，设u为tree点，v为fringe点，未加入x前的生成树为T。我们假设T+e=T'得到的生成树不满足MST性质。既然不满足MST性质，那么一定存在一条边e'（x,y），加入T'后，产生的环中存在权值大于e'的边。

如果x，y都不等于v，那么加入e'产生的环存在于T中，但是T满足MST性质（因为T中只有x-1个点）,所以x,y中一定有一个是v。不妨设y=v。

那么如下图：

如上图，设u到x之间的路径为W1......Wa,Wa+1.....Wb-1,Wb.......Wp,其中W1为u，Wp为x，设边WaWa+1是路径中第一条权值大于e'的边，

Wb-1Wb是最后一条权值大于e'的边（有可能这两条边是同一条）。不妨设WaWa+1先于Wb-1Wb加入到T中，那么由Prim算法的步骤，知W1W2,W2W3.......Wa-1Wa均会先于WaWa+1加入到T'中，进一步由于e先于e’加入到Ｔ中，所以有|e|<=|e'|<|Wb-1Wb|，所以e和e'均会先于WaWa+1加入到T'中，但是事实是，e'并不在T'中，而且它比WaWa+1要晚加入T'中，所以矛盾。所以T'加入e'后，所产生的环中e'的权值最大，满足MST性质。那么当k=n的时候，也就是算法完成的时候，所得到的生成树就是整个图G的生成树，它满足MST性质，由定理1可知，它是最小生成树。证毕。

Kruskal算法：

Kruskal算法同样是基于贪心策略，但是它和Prim算法不同的是，在算法过程中它并不维护一个连通的分量，而是将多个连通分量合并到一起得到一颗生成树。个人觉得Kruskal算法的思想比它算法本身要重要，能够解决很多其他问题，至少是在ACM比赛中吧。

下面描述一下Kruskal算法的步骤：

首先将图中的所有的边按照其权值从小到大排序，然后从小到大枚举边。设需要构造的生成树为T。

1：初始时，Ｔ中没有变，所有点看成是一个单独的集合。

2：如果枚举完最后一条边，则到4，否则到３。

3：设当前枚举的边为e(u,v)，如果u,v不在同一个集合中，则将e加入到T中，并且将u和v合并到一个集合中，否则，忽略e。转到2.

4：如果T中含有n-1条边，则说明找到原图的最小生成树，否则说明原图没有最小生成树。算法结束。

算法的实现需要一些额外的知识，首先是要从小到大枚举边，这里可以用快速排序直接将边集排序，或者可以用小顶堆来初始化边集。

然后是要判断两个点是否在统一集合中，还需要将两个集合合并到一个集合中。这里要用到并查集这一数据结构。这方面的知识请自行参考相关资料。

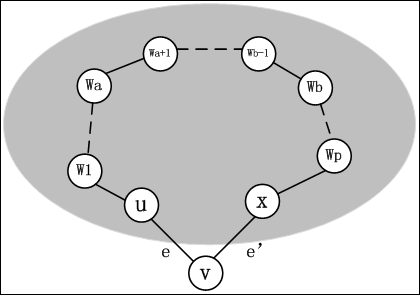
下面是利用快速排序和并查集实现的Kruskal算法。

#define maxn 110
#define maxm 10010
using namespace std;
int uf[maxn];
struct edge{
int u,v,len;
}e[maxm];
bool cmp(const edge &x,const edge &y){
return x.len<y.len;
}
void init(int n){//初始化并查集
for(int i=0;i<=n;i++)uf[i]=i;
}
int find(int x){
if(x==uf[x])return x;
return uf[x]=find(uf[x]);
}
int Union(int x,int y){//合并两个集合（如果x,y在同一集合，返回0，否则返回1）
x=find(x),y=find(y);
if(x!=y){
uf[x]=y;
return 1;
}
return 0;
}
int Kruskal(int n,int m){//n个点，m条边
sort(e,e+m,cmp);//排序
int sum=0;//最小生成树的权值和
for(int i=0;i<m;i++){//从小到大枚举边
int u=e[i].u,v=e[i].v,len=e[i].len;
sum+=len*Union(u,v);
}
return sum;//返回权值和
}

#define maxn 110

#define maxm 10010

using namespace std;

int uf[maxn];

struct edge{

    int u,v,len;

}e[maxm];

bool cmp(const edge &x,const edge &y){

    return x.len<y.len;

}

void init(int n){//初始化并查集

    for(int i=0;i<=n;i++)uf[i]=i;

}

int find(int x){

    if(x==uf[x])return x;

    return uf[x]=find(uf[x]);

}

int Union(int x,int y){//合并两个集合（如果x,y在同一集合，返回0，否则返回1）

    x=find(x),y=find(y);

    if(x!=y){

        uf[x]=y;

        return 1;

    }

    return 0;

}

int Kruskal(int n,int m){//n个点，m条边

    sort(e,e+m,cmp);//排序

    int sum=0;//最小生成树的权值和

    for(int i=0;i<m;i++){//从小到大枚举边

        int u=e[i].u,v=e[i].v,len=e[i].len;

        sum+=len*Union(u,v);

    }

    return sum;//返回权值和

}

Kruskal算法的正确性

同Prim算法正确性证明一样，我们只要证明Kruskal算法得到的生成树满足MST性质即可。首先，如果G存在最小生成树，那么Kruskal算法得到肯定是一颗生成树。这点就不证明了，用反证法可以很容易证明。

定理3：设带全图G(V,E,W)存在最小生成树，那么Kruskal算法得到的生成树就是G的最小生成树。

证明：设Kruskal算法结束时得到的生成树为T，假设T不满足MST性质，那么存在一条边e（u，v），它不属于T，将e加入T中后，得到一个环。设环中存在一条（可能是多条）边e'，其权值大于e。那么由Kruskal算法的步骤，可知，e在e'之前枚举。当枚举e'之前，可知u,v一定不在同一个集合中，否则e'就不会在T中了。那么既然在e'加入之前，u，v不在同一个集合中，那么枚举e时(e在e'加入前被枚举),根据Kruskal算法的步骤3，可知e一定在T中，但是e并不在T中，矛盾，所以加入e后，所得到的环中e的权值最大。这就表示T满足MST性质。从而由定理1，可知T是Ｇ的一颗最小生成树。证毕。

总结：到此为止，最小生成树的总结就写完了，介绍的两个算法都是基于贪心思想的应用。个人觉得学习算法一定不能仅仅记住算法的代码实现，一定还要理解其中的思想和正确性。只有这样才能真正了解一个算法的精髓。就算是忘了代码的实现，理解了思想也能自己推出来。这应该才是学习的不二法门吧。