第二十六章 hystrix-dashboard + turbine

一、使用turbine的意义

引入多个hystrix stream：

1、使用hystrix-dashboard的可以添加多个stream的功能

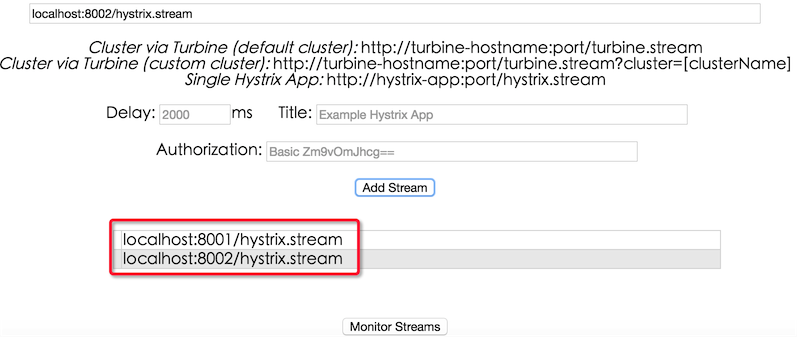
图中添加的两个stream会在真正monitor的时候分开展示，这样的话，假设两个stream都引用了同一个方法a，那么方法a会分开展示两次，如下：

实际上我们只需要统计a的处理能力，与谁调用无关，所以希望在整个dashboard下只有一个a的展示，那么我们就需要通过turbine将这些所有a的展示汇聚起来。

注意：

• turbine的汇聚也是实时的

2、使用turbine进行汇聚

turbine介绍：附7 turbine

turbine部署：第二章 部署war包到tomcat

二、总体图

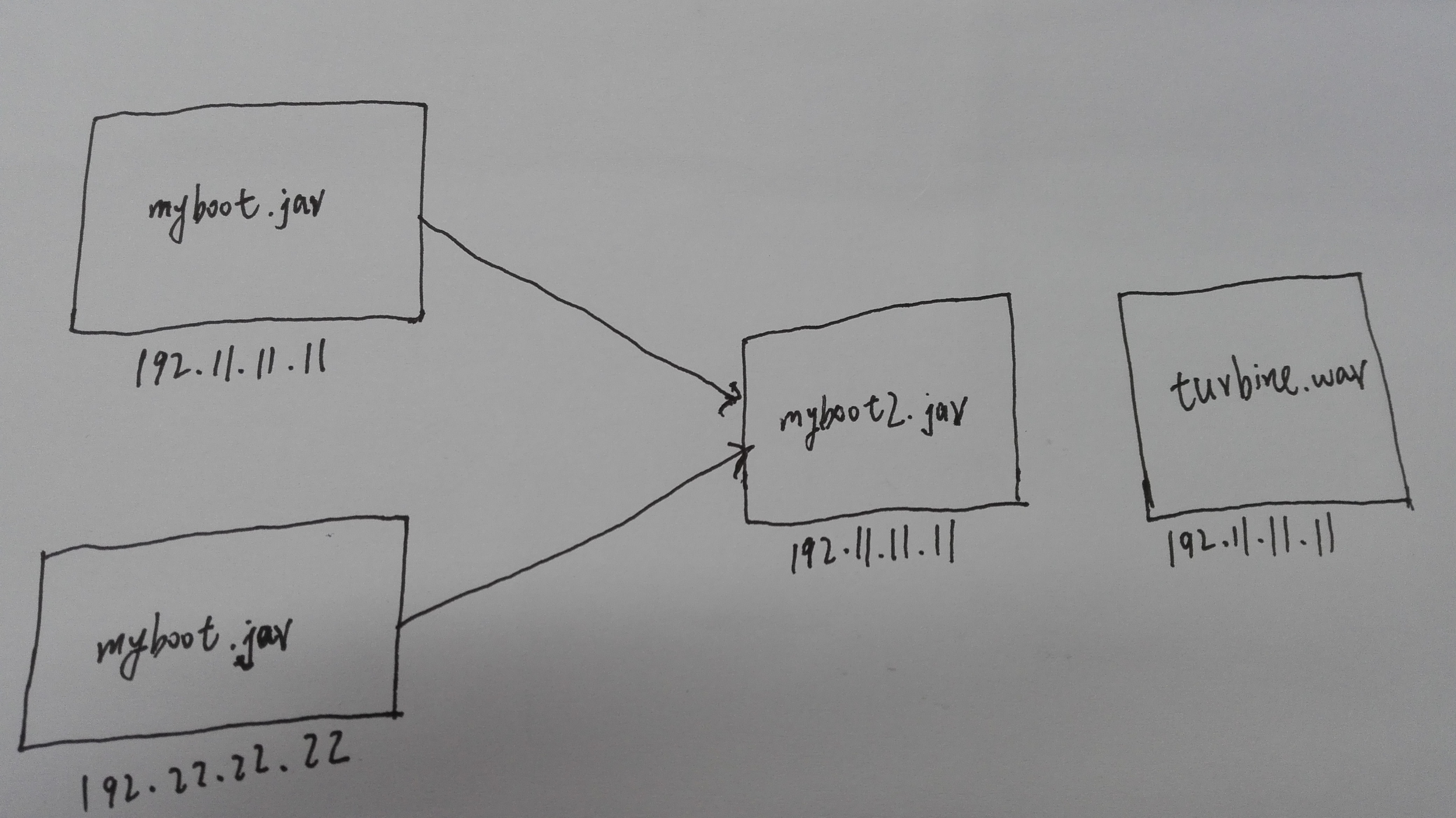
前提：

• 假设有两个服务A/B分别布在两台机器上（这里为了简单，使用一个服务myboot来代替），A、B都访问myboot2的两个接口getHotelInfo和getHotelInfo2（这两个接口也是commandKey的名字）；
• 同时在一台机器上部署了turbine.war。

测试：

• A、B对两个接口getHotelInfo和getHotelInfo2能否分别聚合。

三、操作

1、分别将myboot项目在两台机器上启动

• 会用到的命令：scp myboot.jar root@192.22.22.22:~/zjg/service（将本地的myboot.jar拷贝到远程机器的~/zjg/service目录下）

2、启动myboot2.jar

3、配置tomcat的webapps下的turbine/WEB-INF/classes/config.properties

InstanceDiscovery.impl=com.netflix.turbine.discovery.ConfigPropertyBasedDiscovery
#cluster
turbine.aggregator.clusterConfig=default
#turbine.aggregator.clusterConfig=myboot
turbine.instanceUrlSuffix=:8001/hystrix.stream
turbine.ConfigPropertyBasedDiscovery.default.instances=192.11.11.11,192.22.22.22

说明：配置了一个cluster为default，原因及其他配置见 附7 turbine

4、启动turbine

• 如果需要tomcat的关闭过程可能不会关闭干净，使用ps -ef | grep tomcat，之后进行kill就好。

5、分别启动两台机器上的hystrix-dashboard

6、浏览器输入

• "192.11.11.11:7979/hystrix-dashboard"并添加"192.11.11.11:8001/hystrix.stream"进行monitor
• "192.22.22.22:7979/hystrix-dashboard"并添加"192.22.22.22:8001/hystrix.stream"进行monitor
• "192.11.11.11:7979/hystrix-dashboard"（重新打开一个页面）并添加"192.11.11.11:8080/turbine/turbine.stream"进行monitor

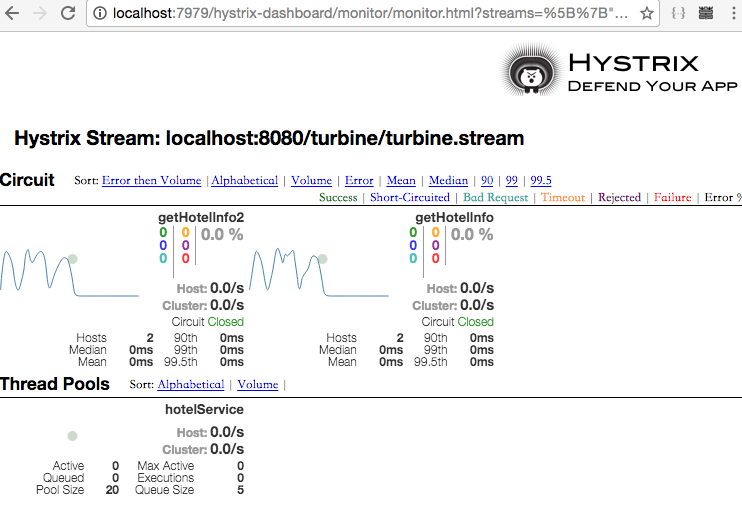
7、使用swagger分别访问myboot调用myboot2的两个接口getHotelInfo和getHotelInfo2，查看3个monitor页面，会发现turbine.stream会是前两个hystrix.stream的聚合结果

四、turbine结果