Luogu 4438 [HNOI/AHOI2018]道路

$dp$。

这道题最关键的是这句话：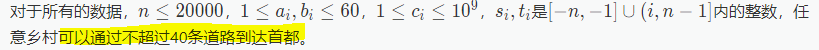

跳出思维局限大胆设状态，设$f_{x, i, j}$表示从$x$到根要经过$i$条公路，$j$条铁路的代价，那么对于一个叶子结点，有$f_{x, i, j} = c_x * (a_x + i) * (b_x + j)$，对于内部结点，有转移：

　　$f_{x, i, j} = min(f_{lson(x), i + 1, j} + f_{rson(x), i, j}, f_{lson(x), i, j}) + f_{rson(x), i, j + 1}$。

然后$40000 * 40 * 40$就快$512MB$了，然后最后一个点就光荣$MLE$了。

所以要写成记搜的，就可以省掉一半$f$数组的空间。

时间复杂度上界是$O(n * 40 * 40)$。

Code：

#include <cstdio>
#include <cstring>
using namespace std;
typedef long long ll;

const int N = ;
const int M = ;
const ll inf = 0x3f3f3f3f3f3f3f3f;

int n, son[N][], a[N], b[N], c[N];
ll f[N][M][M];

template <typename T>
inline void read(T &X) {
    X = ; char ch = ; T op = ;
    for(; ch > ''|| ch < ''; ch = getchar())
        if(ch == '-') op = -;
    for(; ch >= '' && ch <= ''; ch = getchar())
        X = (X << ) + (X << ) + ch - ;
    X *= op;
}

template <typename T>
inline T min(T x, T y) {
    return x > y ? y : x;
}   

ll dfs(int x, int i, int j) {
    if(x >= n)
        return 1LL * c[x - n + ] * (a[x - n + ] + i) * (b[x - n + ] + j);
    if(f[x][i][j] != inf) return f[x][i][j];
    return f[x][i][j] = min(dfs(son[x][], i + , j) + dfs(son[x][], i, j), dfs(son[x][], i, j) + dfs(son[x][], i, j + ));
}

int main() {
//    freopen("road20.in", "r", stdin);

    read(n);
    for(int lc, rc, i = ; i < n; i++) {
        read(lc), read(rc);
        if(lc < ) lc = n -  - lc;
        if(rc < ) rc = n -  - rc;
        son[i][] = lc, son[i][] = rc;
    }

    for(int i = ; i <= n; i++)
        read(a[i]), read(b[i]), read(c[i]);

    memset(f, 0x3f, sizeof(f));
    printf("%lld\n", dfs(, , ));
    return ;
}