BWT (Burrows–Wheeler_transform)数据转换算法

1.什么是BWT

　　压缩技术主要的工作方式就是找到重复的模式，进行紧密的编码。

　　BWT(Burrows–Wheeler_transform)将原来的文本转换为一个相似的文本，转换后使得相同的字符位置连续或者相邻，之后可以使用其他技术如：Move-to-front transform 和 游程编码 进行文本压缩。

2.BWT原理

2.1 BWT编码

　　(1)首先，BWT先对需要转换的文本块，进行循环右移，每次循环一位。可以知道长度为n的文本块，循环n次后重复，这样就得到看n个长度为n的字符串。如下图中的“Rotate Right”列。（其中‘#’作为标识符，不在文本块的字符集中，这样保证n个循环移位后的字符串均布相同。并且定义'#'小于字符集中的任意字符）。

　　 (2)对循环移位后的n个字符串按照字典序排序。如下图中的“Sorted (M)”列。

　　 (3)记录下“Sorted (M)”列中每个字符串的最后一个字符，组成了“L”列。(其中"F"列是“Sorted (M)”列中每个字符串的前缀)

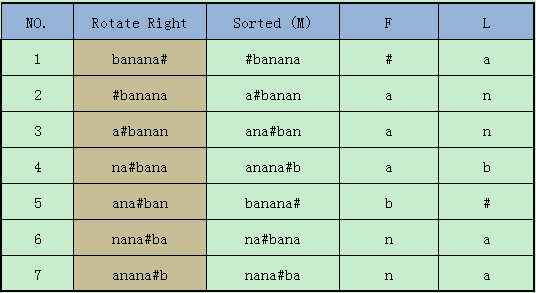
　　这样，原来的字符串“banana#”就转换为了“annb#aa”。在某些情况下，使用L列进行压缩会有更好的效果。“L”列就是编码的结果。

2.2 BWT解码

　　因为进行的是循环移位，且是循环左移注意下面的性质：

    　　1、L的第一个元素是Text中的最后一个元素

    　　2、对于M中的每一行（第一行除外）第一个元素都是最后一个元素的下一个元素。

　　　　  也就是说，对于文本块而言，同一行中F是L的下一个元素，L是F的前一个元素。

 

　　这样，就需要

　　(1)通过"F"列中的元素，找到他前面的字符，就是对应的同一行“L”列；

　　(2)通过“L”列中的元素，找到他在“F”列中的对应字符位置。但是“L”中有3个字符a，如何对应F中的3个a呢？因为L是F的前一个元素，多个具有相同前缀的字符串排序，去掉共同前缀后相对次序没有变化。所有遇到多个相同的字符，相对位置不变；

　　(3)转到(1)，直到结束。

　　因为F列是已经排序的，可以从L列获得，所有只需要保存L列就可以。从L列中的字符获取在F列中的位置时，需要：

　　(1)前缀和数组，记录小于当前字符的字符数个数。

　　(2)count计数，计算L中从开始位置到当前字符位置等于该字符的字符数。(保证多个相同字符下"L"到“F”的相对位置不变)。

3.BWT文本块编码、解码实例

 #include <iostream>
 #include <string>
 #include <algorithm>
 #include <string.h>
 using namespace std;
 
 ///编码，生成last数组
 int getLastArray(char *lastArray,const string &str){    ///子串排序
     int len=str.size();
     string array[len];
 
     for(int i=;i<len;i++){
         array[i] = str.substr(i);
     }
     sort(array,array+len);
     for(int i=;i<len;i++){
         lastArray[i] = str.at((*len-array[i].size()-)%len);
     }
     return ;
 }
 
 int getCountPreSum(int *preSum,const string &str){
     memset(preSum,,*sizeof(int));
     for(int i=;i<str.size();i++){
         if(str.at(i) == '#')
             preSum[]++;
         else
             preSum[str.at(i)-'a'+]++;
     }
 
     for(int i=;i<;i++)
         preSum[i] += preSum[i-];
     return ;
 }
 
 ///解码，使用last数组，恢复原来的文本块
 int regainTextFromLastArray(char *lastArray,char *reGainStr,int *preSum){
     int len=strlen(lastArray);
     int pos=;
     char c;
     for(int i=len-;i>=;){
         reGainStr[i] = lastArray[pos];
         c = lastArray[pos];
         pos = preSum[c-'a']+count(lastArray,lastArray+pos,c);
         i--;
     }
     return ;
 }
 
 int main (){
     string str("sdfsfdfdsdfgdfgfgfggfgdgfgd#");
     int preSum[];
     int len=str.size();
 
     char *lastArray = new char[len+];
     char *reGainStr = new char[len+];
     lastArray[len]='\0';
     reGainStr[len]='\0';
 
     getCountPreSum(preSum,str);
     getLastArray(lastArray,str);
     regainTextFromLastArray(lastArray,reGainStr,preSum);
 
     cout<<"       str: "<<str<<endl;
     cout<<"lastArray : "<<lastArray<<endl;
     cout<<"reGainStr : "<<reGainStr<<endl;
 
     delete lastArray;
     delete reGainStr;
     return ;
 }

代码执行输出：

参考：

http://en.wikipedia.org/wiki/Burrows%E2%80%93Wheeler_transform

http://emily2ly.iteye.com/blog/742869

额外阅读：

MTF(Move-to-front transform)数据转换

基于统计的压缩算法：游程编码