CF735D Taxes 哥德巴赫猜想\判定素数 \进一步猜想

http://codeforces.com/problemset/problem/735/D

题意是。。一个数n的贡献是它的最大的因子，这个因子不能等于它本身

然后呢。。现在我们可以将n拆成任意个数的整数相加，每个数最小只能拆成2,

单独计算每个数的贡献，然后加起来使他的贡献最小。。那么我们肯定是拆成质数最赚

因为质数对答案的贡献是1...

所以现在这个问题变成了把一个数拆成最少个数的质数

那么我们不知道最少能拆成多少个质数啊。。
我一开始想的是你每次找最接近这个数的质数。。一直找下去应该是可以的。。但是我不知道最后剩下一个合数怎么办

也不知道这种情况会不会发生

到这里我没有探索也没有画图就放弃了。。因为我发现。。预处理2e9的素数好像不太可能啊。。不过这里有个隐藏的前提

那就是如果预处理2e9的素数是必须的话。。那我们无法做到。。那么就不用做这个题了。。但是我们现在并不确定题目的

解法是一定需要这个预处理的。。所以我们可以选择继续探索

Tip：当你无法解决手头的问题。。那么你可以去找一道相似的题目或者分解成一些子问题去一道一道地做

先解决其他的题目

对于2，本身就是质数不用分解

对于3，本身就是质数不用分解

对于4，可以分解成2,2 因为题目要求最小是2，这里如果忘记不回顾的话。。很炸，要习惯性地检查题目的条件

对于5，可以分解成2,3

对于6，可以分解成3,3

对于7，可以分解成3,2,2

对于8，可以分解成5,3

对于9，可以分解成2,7

对于10，可以分解成5,5

这样枚举很累的。。我们写程序打一个表

打表的程序如下所示

#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
bool check(int x){
    int i;//小心爆int
    for(i=;i*i<=x;++i){
        if(x%i==) return false;
    }
    return true;
}
int rec[];
int cur;
bool fnd;
void dfs(int x,int dep){
    int i;
    if(x==) return;
    if(x==){
        printf("val:%d--",cur);
         for(i=;i<dep;++i){
             printf("%d ",rec[i]);
         }
         printf("\n");
         fnd=true;
         return;
    }
    for(i=x;i>=&&!fnd;--i){
        rec[dep]=i;
        if(i==||check(i))
        dfs(x-i,dep+);
    }
}
int n;
int main(){
    scanf("%d",&n);
    int i;
    for(i=;i<=n;++i){
        fnd=false;
        cur=i;
        dfs(i,);
    }
    return ;
}

打表之后我们发现了一个很大的问题。。

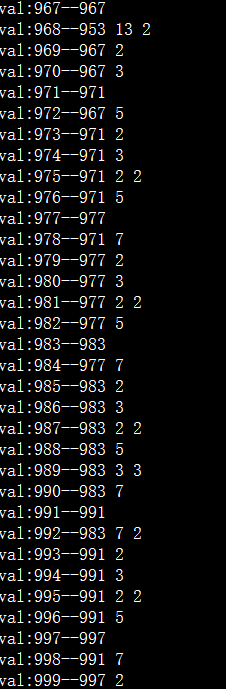
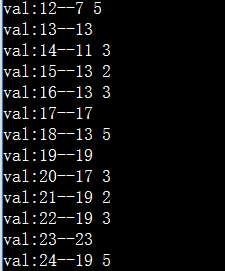
最多不超过3个数。。

我们再观察一下奇偶性。。然后就能发现。。偶数总是能分解成两个质数

从表中看出。。这些质数距离不太固定。。因此你每次找最近的质数。。应当是不太对的哦

既然偶数总是能分解成两个质数，不相信的话我们可以专门打一个表啊

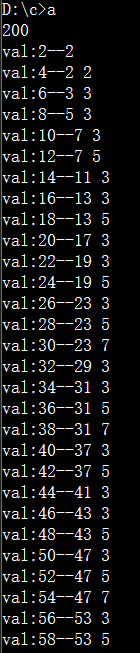
全部是两项。。

那么对于偶数。。特判2就可以得到结果了

但是对于奇数呢。。由于最小的项为2。。。我们不能

考虑-1，然后分解一个偶数。。

我们要考虑-2之后是一个什么情况。。奇数减去2之后仍然是一个奇数

如果这时它是一个质数。。那么我们就已经成功地把这个数分解成了两个质数

如果这时它不是一个质数。。那么我们仍然把它看成奇数。。分出一个1来。。剩下的一个偶数就能分解成两个质数

分出来的这个1和减去的2合并成3,哈哈。。正好3也是一个质数。。要不然说不定要构造一个质数呢

3是一个质数。。而剩下的那个偶数可以分解成两个质数。。一共三个质数

最后我们还要考虑不用分解的情况。。它本身就是一个质数你还分解它干什么。。

通过这个题我们可以看出来打表看规律是解决数论问题的一个非常重要的手段

并且我们要熟悉快速打表。。而且打表也不是一定正确的。。对于我们发现的一个偶数一定能分解成两个质数这个结论

他是一个哥德巴赫猜想。。我们可以认为在ll内它都是正确的。。并且根据群巨打表的情况在ll范围内。。相邻两个

素数的最大距离gap大概是778...所以说暴力找的话也是很好找的

代码虽然简单。。但是思路却要开阔，敢于探索。。不能太笨纯手推。。答案来之不易啊