混沌数学之Duffing(杜芬)振子
杜芬振子 Duffing oscillator是一个描写强迫振动的振动子,由非线性微分方程表示
杜芬方程列式如下:

其中
- γ控制阻尼度
- α控制韧度
- β控制动力的非线性度
- δ驱动力的振幅
- ω驱动力的圆频率
杜芬方程没有解析解,但可用龙格-库塔法求得数值解。
当γ>0,杜芬振子呈现极限环振动;
相关软件:混沌数学及其软件模拟
相关代码:
//http://wenku.baidu.com/view/d51372a60029bd64783e2cc0.html?re=view
class DuffingEquation : public DifferentialEquation
{
public:
DuffingEquation()
{
m_StartX = 1.0f;
m_StartY = 1.0f;
m_StartZ = 0.0f; m_ParamA = 2.09f;
m_ParamB = 0.1f;
m_ParamC = 0.5f; m_StepT = 0.002f;
} void Derivative(float x, float y, float z, float& dX, float& dY, float& dZ)
{
dX = y;
dY = m_ParamA*cosf(m_ParamC*m_ParamT) - m_ParamB*y + x - x*x*x;
dZ = 0.0f;
} bool IsValidParamA() const {return true;}
bool IsValidParamB() const {return true;}
bool IsValidParamC() const {return true;}
bool IsValidParamT() const {return true;}
};
相关截图:
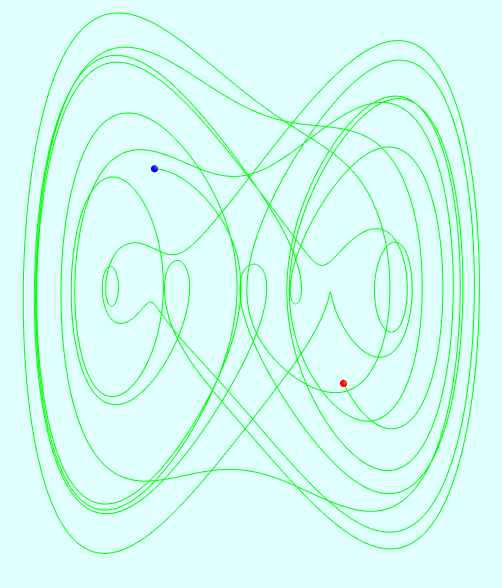
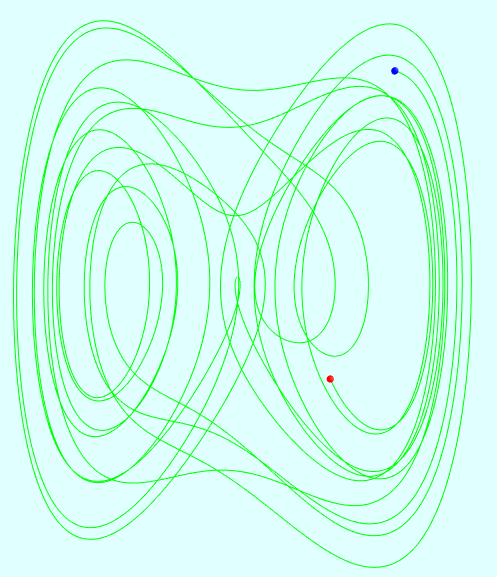



混沌数学之Duffing(杜芬)振子的更多相关文章
- 混沌数学之Lorenz(洛伦茨)吸引子
洛伦茨吸引子是洛伦茨振子(Lorenz oscillator)的长期行为对应的分形结构,以爱德华·诺顿·洛伦茨的姓氏命名. 洛伦茨振子是能产生混沌流的三维动力系统,是一种吸引子,以其双纽线形状而著称. ...
- 混沌数学之Chua's circuit(蔡氏电路)
蔡氏电路(英语:Chua's circuit),一种简单的非线性电子电路设计,它可以表现出标准的混沌理论行为.在1983年,由蔡少棠教授发表,当时他正在日本早稻田大学担任访问学者[1].这个电路的制作 ...
- 混沌数学之logistic模型
logistic回归又称logistic回归分析,主要在流行病学中应用较多,比较常用的情形是探索某疾病的危险因素,根据危险因素预测某疾病发生的概率. 相关DEMO参见:混沌数学之离散点集图形DEMO ...
- 混沌数学之Henon吸引子
Henon吸引子是混沌与分形的著名例子. 相关软件:混沌数学及其软件模拟相关代码: // http://wenku.baidu.com/view/d51372a60029bd64783e2cc0.ht ...
- 混沌数学之拉比诺维奇-法布里康特方程(Rabinovich-Fabrikant equations)
拉比诺维奇-法布里康特方程(Rabinovich-Fabrikant equations)是 1979年苏联物理学家拉比诺维奇和法布里康特提出模拟非平衡介 质自激波动的非线性常微分方程组: dot{x ...
- 混沌数学之Rössler(若斯叻)吸引子
若斯叻吸引子(Rössler attractor)是一组三元非线性微分方程: frac{dx(t)}{dt} = -y(t)-z(t) frac{dy(t)}{dt} = x(t)+a*y(t) fr ...
- 混沌数学之ASin模型
相关软件:混沌数学之离散点集图形DEMO 相关代码: class ASinEquation : public DiscreteEquation { public: ASinEquation() { m ...
- 混沌数学之Kent模型
相关软件:混沌数学之离散点集图形DEMO 相关代码: // http://wenku.baidu.com/view/7c6f4a000740be1e650e9a75.html // 肯特映射 clas ...
- 混沌数学之Feigenbaum模型
1975年,物理学家米切尔·费根鲍姆(Mitchell Feigenbaum)发现,一个可用实验加以测 量的特殊数与每个周期倍化级联相联系.这个数大约是4.669,它与π并列成为似乎在数学 ...
随机推荐
- 1021 Deepest Root (25)(25 point(s))
problem A graph which is connected and acyclic can be considered a tree. The height of the tree depe ...
- python ftp操作脚本&常用函数
需求:快速进行ftp上传 ,下载,查询文件 原来直接在shell下操作: 需要[连接,输用户名,输密码,单文件操作,存在超时限制] 太过于繁琐,容易操作失败 脚本改进: 一句命令,搞定多文件上传,下载 ...
- Hibernate与Mybatis对比
Hibernate与Mybatis对比 两者相同点 Hibernate与MyBatis都可以是通过SessionFactoryBuider由XML配置文件生成SessionFactory,然后由Ses ...
- luoguP3871 [TJOI2010]中位数
题目链接 luoguP3871 [TJOI2010]中位数 题解 平衡树 代码 #include<vector> #include<cstdio> #include<cs ...
- Tomcat CVE-2017-12615 远程上传漏洞复现
漏洞名称:CVE-2017-12615-远程代码执行漏洞 CVE-2017-12615:远程代码执行漏洞 当 Tomcat运行在Windows操作系统时,且启用了HTTP PUT请求方法(例如,将 r ...
- 压缩的问题-----WriteUp
原题:http://ctf5.shiyanbar.com/crypto/winrar/ 526172211A0700CF907300000D0000000000000056947424965E 006 ...
- hdu 5316 Magician(2015多校第三场第1题)线段树单点更新+区间合并
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5316 题意:给你n个点,m个操作,每次操作有3个整数t,a,b,t表示操作类型,当t=1时讲a点的值改 ...
- python调用matlab
官网链接: https://ww2.mathworks.cn/help/matlab/matlab_external/call-user-script-and-function-from-python ...
- 解耦你的HTML,CSS和JAVASRIPT
注:本文为翻译文章,原文<Decoupling Your HTML, CSS, and JavaScript> 今天在web上任何大一点的网站或应用程序都包含大量的html,css和jav ...
- Educational Codeforces Round 13 B. The Same Calendar 水题
B. The Same Calendar 题目连接: http://www.codeforces.com/contest/678/problem/B Description The girl Tayl ...
