TensorFlow.NET机器学习入门【2】线性回归

回归分析用于分析输入变量和输出变量之间的一种关系，其中线性回归是最简单的一种。

设： Y=wX+b，现已知一组X（输入）和Y（输出）的值，要求出w和b的值。

举个例子：快年底了，销售部门要发年终奖了，销售员小王想知道今年能拿多少年终奖，目前他大抵知道年终奖是和销售额（特征量）挂钩的，具体什么规则不清楚，那么他大概有两个方法解决这个问题：

1、去问老板，今年的分配规则是什么。【通过算法解决问题】

2、去向同事打听他们的销售额和奖金情况，然后推算自己能拿多少。【通过数据解决问题】

我们当然选择第二种方法了。通过收集数据，我们得到下面这个表格：

拿到这个数据，我们基本上很快就能推算出两者的对应关系，如果推算不出来，我们也可以绘制下面这张图表：

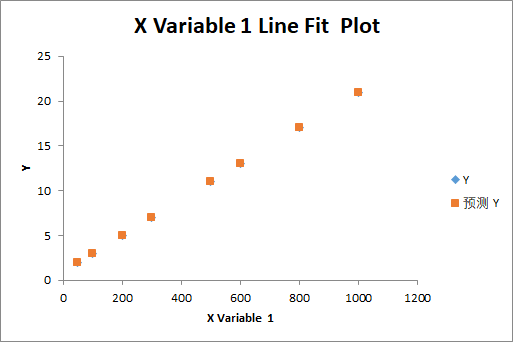
通过图表，我们可以立即看出两者的对应关系了。

以上就是一个典型的线性回归求解的问题，下面我们要用TensorFlow框架解决这个问题。

具体解决思路如下：

1、先设w=1，b=0

2、取得一批训练数据，将X代入函数f(x)=wx+b，计算取得在当前条件下的预测值Y‘

3、计算预测值Y‘和实际值Y的误差

4、根据梯度对w、b进行微调

5、重复上述步骤，直到误差值足够小。

先贴出全部代码，然后再逐一解释。

   public class LinearRegression
    {
        public void Run()
        {
            // Supper Parameters
            float learning_rate = 0.01f;

            var W = tf.Variable<float>(1);
            var b = tf.Variable<float>(0);

            int epochs = 30;
            int steps = 100;
            Tensor loss = null;

            for (int epoch = 0; epoch < epochs; epoch++)
            {
                for (int step = 0; step < steps; step++)
                {
                    int batch_size = 10;
                    (NDArray train_X, NDArray train_Y) = LoadBatchData(batch_size);

                    using (var g = tf.GradientTape())
                    {
                        //通过当前参数计算预测值
                        var pred_y = W * train_X + b;

                        //计算预测值和实际值的误差
                        loss = tf.reduce_sum(tf.pow(pred_y - train_Y, 2)) / batch_size;

                        //计算梯度
                        var gradients = g.gradient(loss, (W, b));

                        //更新参数
                        W.assign_sub(learning_rate * gradients.Item1);
                        b.assign_sub(learning_rate * gradients.Item2);
                    }
                }

                Console.WriteLine($"Epoch{epoch + 1}: loss = {loss.numpy()}; W={W.numpy()},b={b.numpy()}");
            }
        }

        public (NDArray, NDArray) LoadBatchData(int n_samples)
        {
            float w = 0.02f;
            float b = 1.0f;

            NDArray train_X = np.arange<float>(start: 1, end: n_samples + 1);
            NDArray train_Y = train_X * w + b;

            return (train_X, train_Y);
        }
    }

下面对代码进行简单的解释：

首先，我们要读取一批（比如10组 ）训练数据，标记为：train_X和train_Y，然后通过现有的w和b值计算预测值：pred_Y=w*train_X_b，此时train_X、train_Y、pred_Y都是10个数据长度的数组。

然后计算预测数据和时间数据之间的误差，我们采用均方误差公式来计算：

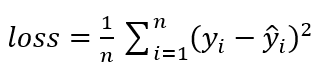
然后开始计算W、b对于loss函数的梯度，梯度表达的就是W、b的变化对计算结果的影响，比如将W增大一点，loss的计算结果是变大还是变小，我们的目标是希望loss的值最小，如果w变大时loss变大（梯度为正数），那么我们下一次就将w变小一点，反之同理。

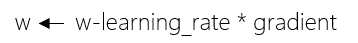
这里的learning_rate表示学习率，表示每次参数进行调整的步进值，就是每次调整一大步，还是一小步。通过多次的循环调整，w和b的值将调整为一个合适的数字，此时loss的值将会很小，线性回归就完成了。以下是运算结果：

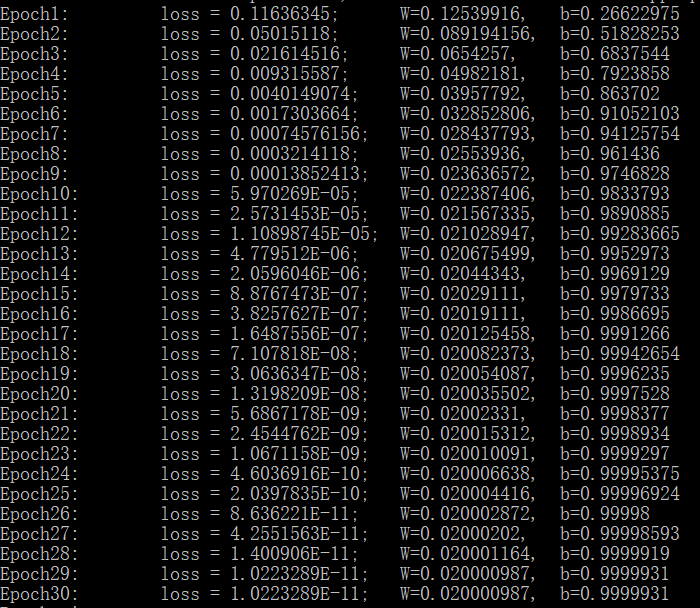
在上述过程中，最难理解的就是梯度，以及如何计算梯度的问题，想要进一步了解的话可以参阅相关参考资料。

【相关资源】

源码：Git: https://gitee.com/seabluescn/tf_not.git

项目名称：LinearRegression

目录：查看TensorFlow.NET机器学习入门系列目录

【参考资料】

《深度学习入门：基于Python的理论与实践（斋藤康毅）》，网上可以找到电子版