Distillation as a Defense to Adversarial Perturbations against Deep Neural Networks

目录

• 概
• 主要内容
  • 算法
  • 一些有趣的指标
    • 鲁棒性定义
    • 合格的抗干扰机制

Nicolas Papernot, Patrick McDaniel, Xi Wu, Somesh Jha, Ananthram Swami, Distillation as a Defense to Adversarial Perturbations against Deep Neural Networks.

概

本文提出一种distillation model, 能够免疫大部分的adversarial attacks, 具有良好的鲁棒性, 同时容易训练.

主要内容

符号	说明
\(F(\cdot)\)	神经网络, 且\(F(X)=\mathrm{softmax^*}(Z(X))\).
\(X \in \mathcal{X}\)	样本
\(Y\)	样本对应的标签
\(F^d\)	distilled network
\(T\)	temperature

注: 这里的\(\mathrm{softmax}^*(z)_i:=\frac{e^{z_i/T}}{\sum_j e^{e_j/T}}, i= 0,\ldots, N-1\);

注: \(F^d\)与\(F\)网络结构一样;

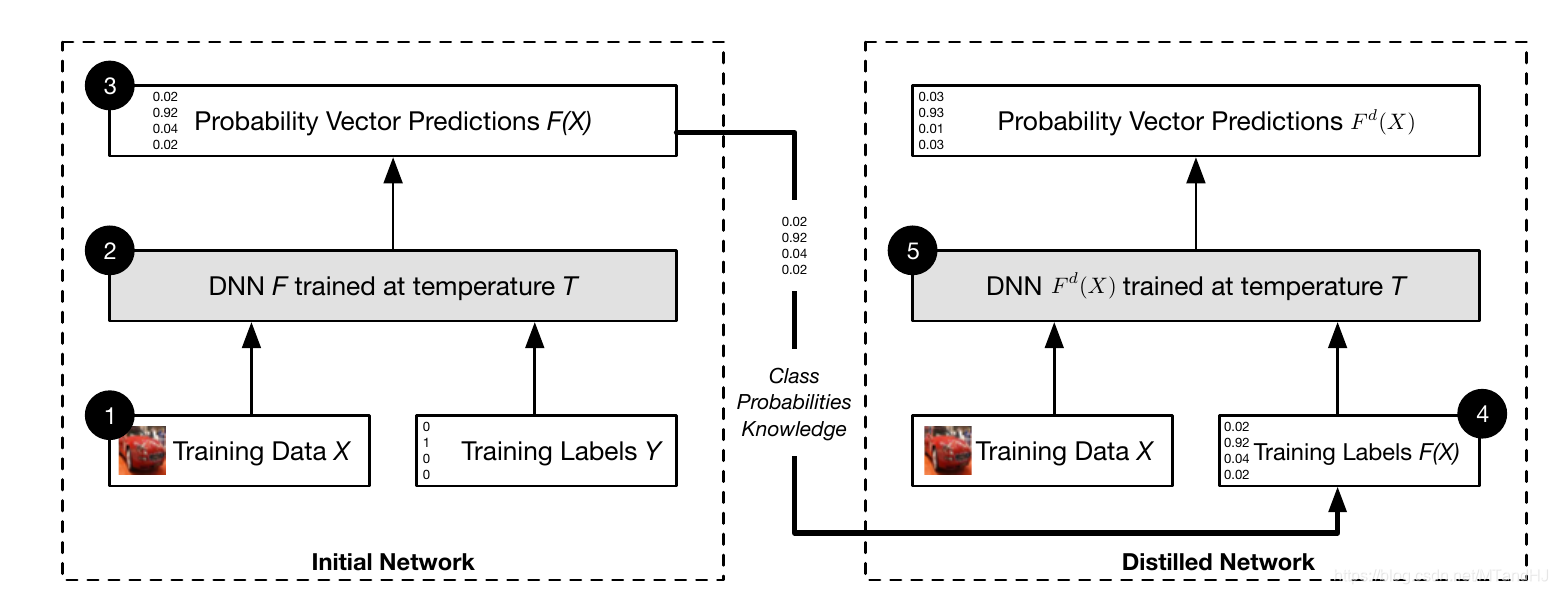
算法

Input: \(T\)，训练数据\((X,Y)\).

• 在训练数据\((X, Y)\)上训练得到\(F\);
• 得到新的训练数据\((X, F(X))\);
• 利用\((X, F(X))\)训练\(F^d\);
• 修改\(F^d\)的最后一层\(T=1\).

Output: \(F^d\).

为什么这个算法是有效的呢?

1. 训练\(F^d\)用的标签是概率向量\(F(X)\), 拿数字举例, 如果写的草一点\(7\)和\(1\)是很相近的, 但如果训练的标签是\((0,0,0,0,0,0,1,0,0,0)\)的话反而不符合实际, 会导致不稳定;
2. 当\(T\)比较大的时候(训练):

\[\frac{\partial F_i(X)}{\partial X_j}|_T = \frac{1}{T}\frac{e^{z_i / T}}{g^2(X)}\big( \sum_{l=1^N}(\frac{\partial z_i}{\partial X_j}-\frac{\partial z_l}{\partial X_j})e^{z_l /T}\big),
\]

会比较小， 其中\(g(X)=\sum_{l=0}^{N-1} e^{z_l(X)/T}\).

3. 在测试的时候, 我们令\(T=1\), 假设\(X\)在原先情况下\(z_1/T\)最大, \(z_2/T\)次大, 则

\[\epsilon=z_2/T-z_1/T= 0 + \mathbf{Tr}(\mathcal{G}^T \delta X) + o(\delta x),
\]

则

\[T\epsilon=z_2-z_1= 0 + T \cdot \mathbf{Tr}(\mathcal{G}^T \delta X) + o(\delta x),
\]

其中\(\mathcal{G}\)为\(z_2-z_1\)在\(X\)处的负梯度.

一些有趣的指标

鲁棒性定义

\[\rho_{adv}(F)= E_{\mu}[\Delta_{adv}(X,F)],
\]

其中\(\mu\)为样本的分布

\[\Delta_{adv}(X,F) = \arg \min_{\delta X} \{ \| \delta X\| : F(X+\delta X) \not = F(X) \}.
\]

可采用下式来实际估计

\[\rho_{adv}(F) \approx \frac{1}{|\mathcal{X}|} \sum_{X \in \mathcal{X}} \min _{\delta X} \|\delta X\|.
\]

合格的抗干扰机制

1. 对原有结构有较少的影响;
2. 网络对干净数据因具有相当的正确率;
3. 较好的训练速度;
4. 对\(\| \delta X\|\)较小的情况能够免疫干扰.

原文还有一个理论分析, 但我认为不重要, 略过.

import torch.nn as nn

class Tsoftmax(nn.Module):

    def __init__(self, T=100):
        super(Tsoftmax, self).__init__()
        self.T = T

    def forward(self, x):
        if self.train():
            return nn.functional.softmax(x / self.T)
        else:
            return nn.functional.softmax(x)