Huffman算法

一、Huffman算法介绍

　　霍夫曼编码（英语：Huffman Coding），又译为哈夫曼编码、赫夫曼编码，是一种用于无损数据压缩的熵编码（权编码）算法。在计算机数据处理中，霍夫曼编码使用变长编码表对源符号（如文件中的一个字母）进行编码，其中变长编码表是通过一种评估来源符号出现几率的方法得到的，出现几率高的字母使用较短的编码，反之出现几率低的则使用较长的编码，这便使编码之后的字符串的平均长度、期望值降低，从而达到无损压缩数据的目的。

　　霍夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。

　　前缀代码表示以一种方式分配代码（位序列），以使分配给一个字符的代码不是分配给任何其他字符的代码的前缀。这就是霍夫曼编码如何确保在解码生成的比特流时没有歧义的地方。

　　让我们通过一个反例来了解前缀代码。假设有四个字符a，b，c和d，它们对应的可变长度代码分别为00、01、0和1。由于分配给c的代码是分配给a和b的代码的前缀，因此这种编码会产生歧义。如果压缩的比特流是0001，则解压缩的输出可以是“ cccd”或“ ccb”或“ acd”或“ ab”。

　　霍夫曼编码主要包括两个主要部分：

　　1）根据输入字符构建霍夫曼树。

　　2）遍历霍夫曼树并将代码分配给字符。

二、构建霍夫曼树的步骤

　　输入是唯一字符及其出现频率的数组，输出是霍夫曼树。

　　1. 为每个唯一字符创建一个叶节点，并为所有叶节点建立一个最小堆（Min Heap用作优先级队列。frequency字段的值用于比较最小堆中的两个节点。最初，把最不频繁的字符作为根）

　　2. 从最小堆中提取频率最小的两个节点。

　　3. 创建一个频率等于两个节点频率之和的新内部节点。使第一个提取的节点为其左子节点，另一个提取的节点为其右子节点。将此节点添加到最小堆中。

　　4. 重复步骤2和3，直到堆仅包含一个节点。其余节点是根节点，树已完成。

　　一个例子：

字符	A	B	C	D	E
频率	1	7	6	5	2

　　步骤1：构建一个包含5个节点的最小堆，其中每个节点代表具有单个节点的树的根。

　　步骤2：从最小堆中提取两个最小频率节点。添加一个频率为1 + 2 = 3的新内部节点。

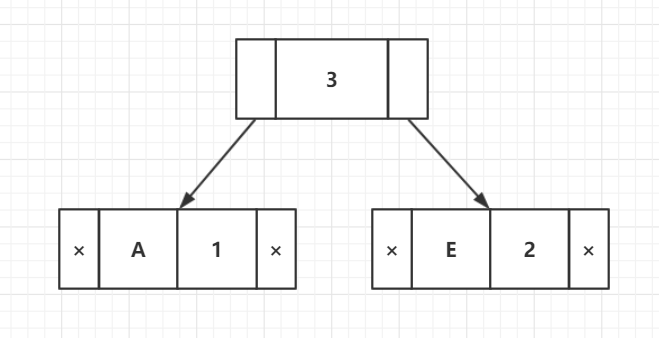
　　现在最小堆包含4个节点，其中3个节点是每个具有单个元素的结点，一个堆节点是具有3个元素。

字符	频率
内部节点	3
D	5
C	6
B	7

　　步骤3：从堆中提取两个最低频率节点。添加频率为12 + 13 = 25的新内部节点

　　现在最小堆包含3个节点，其中2个节点是每个具有单个元素的节点，两个堆节点是具有多个节点的子树。

字符	频率
内部节点	8
C	6
B	7

　　步骤4：提取两个最低频率节点。添加频率为6 + 7 = 13的新内部节点

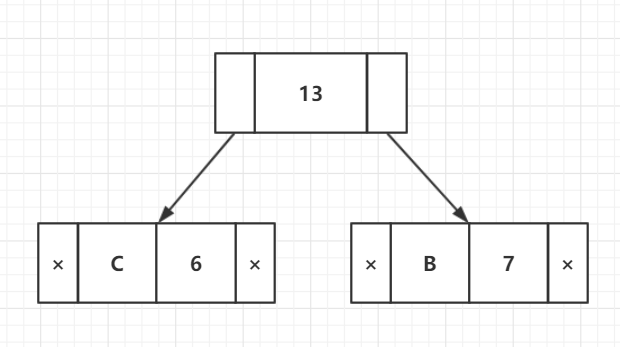
　　现在，最小堆包含2个节点。

字符	频率
内部节点	8
内部节点	13

　　步骤6：提取两个最低频率节点。添加频率为8 + 13 = 21的新内部节点

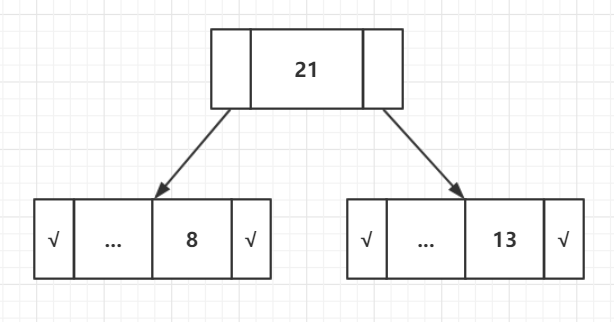
　　现在最小堆中只剩下一个节点，因此算法在此处停止。

　　从霍夫曼树打印代码的步骤：

　　遍历从根开始形成的树。维护一个辅助阵列。当移到左孩子时，将0写入数组。当移动到正确的孩子时，将1写入数组。遇到叶节点时打印阵列。

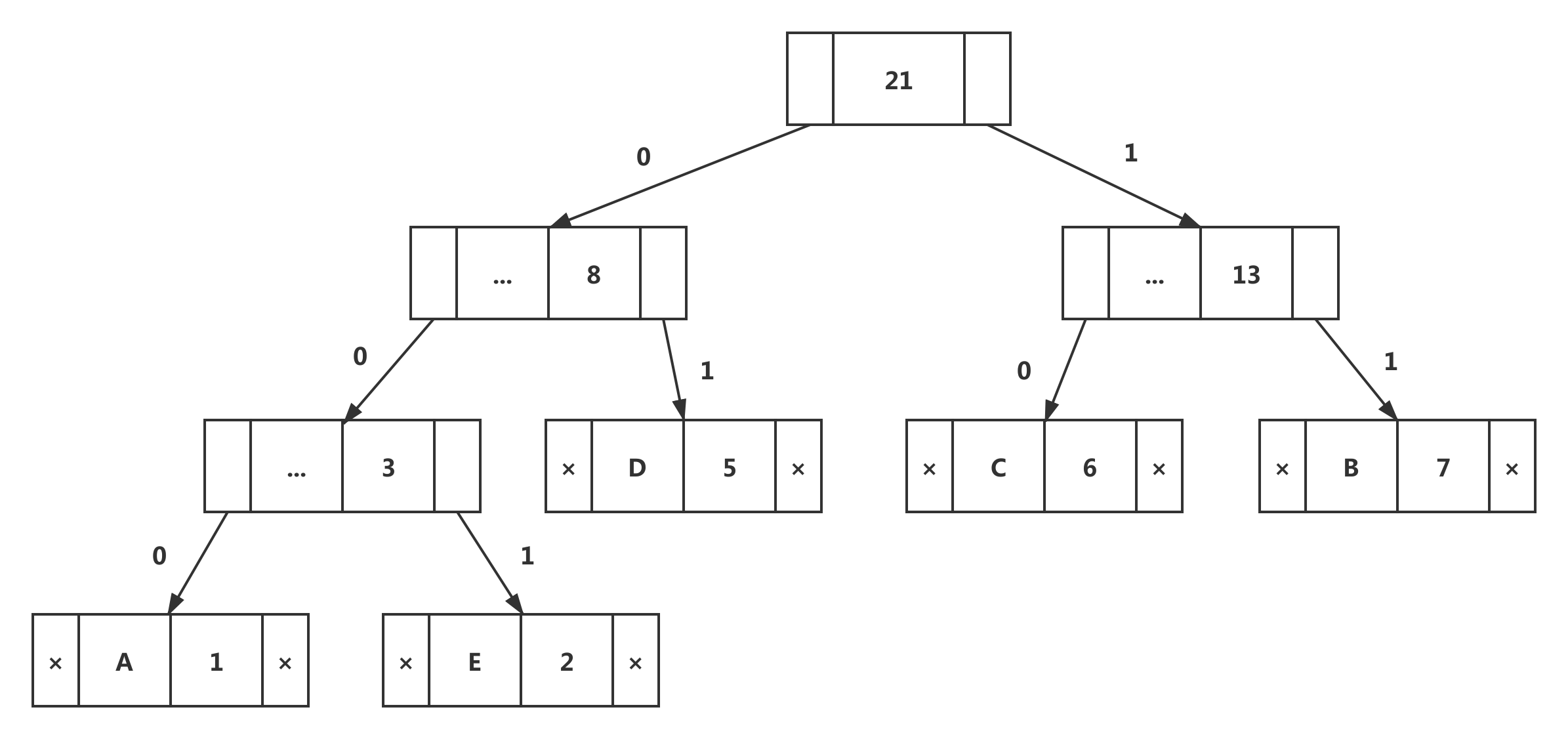
　　输出如下：

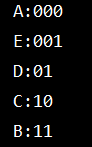
源代码：

  1 package tree;
  2
  3 import java.util.Comparator;
  4 import java.util.PriorityQueue;
  5
  6 /**
  7  * 这是一个哈夫曼树 (Huffman Tree)，用于无损数据压缩的熵编码算法
  8  * 哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。
  9  */
 10 public class HuffmanTree {
 11
 12     /**
 13      * 通过树遍历的霍夫曼代码
 14      * @param root
 15      * @param s
 16      */
 17     public static void printCode(HuffmanNode root, String s) {
 18         /* 如果左右为空，那么这就是一个叶子结点 */
 19         if (root.left == null && root.right == null && Character.isLetter(root.c)) {
 20             System.out.println(root.c + ":" + s);
 21             return;
 22         }
 23         assert root.left != null;
 24         printCode(root.left, s + "0");
 25         printCode(root.right, s + "1");
 26     }
 27
 28     public static void main(String[] args) {
 29
 30         int n = 5;  // 字符数量
 31
 32         /* 下面那个例子的最后结果：
 33             A:000
 34             E:001
 35             D:01
 36             C:10
 37             B:11
 38         */
 39         char[] charArray = {'A', 'B', 'C', 'D', 'E'};
 40         int[] charfreq = {1, 7, 6, 5, 2};
 41
 42         /* 创建优先级队列q，创建一个最低优先级队列（min-heap）。*/
 43         PriorityQueue<HuffmanNode> q = new PriorityQueue<>(n, new MyComparator());
 44
 45         /* 为每个字符创建一个Huffman树的叶子结点，并 */
 46         for (int i = 0; i < n; i++) {
 47             /* 创建一个Huffman节点对象，并将其添加到优先级队列。*/
 48             HuffmanNode hn = new HuffmanNode();
 49
 50             hn.c = charArray[i];
 51             hn.data = charfreq[i];
 52
 53             hn.left = null;
 54             hn.right = null;
 55
 56             q.add(hn);
 57         }
 58
 59         /* 创建一个Huffman根节点 */
 60         HuffmanNode root = null;
 61
 62         while (q.size() > 1) {
 63             /* 提取第一个最小的。*/
 64             HuffmanNode x = q.peek();
 65             q.poll();
 66
 67             /* 提取第二个最小的。*/
 68             HuffmanNode y = q.peek();
 69             q.poll();
 70
 71             /* 新建一个新结点，将两个节点的频率之和分配给f节点 */
 72             HuffmanNode f = new HuffmanNode();
 73             f.data = x.data + y.data;
 74             f.c = '-';
 75
 76             f.left = x;
 77             f.right = y;
 78
 79             root = f;
 80
 81             q.add(f);
 82         }
 83
 84         printCode(root, "");
 85     }
 86 }
 87
 88 /**
 89  * 哈夫曼节点
 90  */
 91 class HuffmanNode {
 92     int data;
 93     char c;
 94
 95     HuffmanNode left;
 96     HuffmanNode right;
 97 }
 98
 99 /**
100  * 用于比较哈夫曼节点值的大小
101  */
102 class MyComparator implements Comparator<HuffmanNode> {
103
104     @Override
105     public int compare(HuffmanNode o1, HuffmanNode o2) {
106         return o1.data - o2.data;
107     }
108 }