NOIP 2017 逛公园 记忆化搜索 最短路 好题

题目描述：

策策同学特别喜欢逛公园。公园可以看成一张N个点MM条边构成的有向图，且没有 自环和重边。其中1号点是公园的入口，N号点是公园的出口，每条边有一个非负权值， 代表策策经过这条边所要花的时间。

策策每天都会去逛公园，他总是从1号点进去，从N号点出来。

策策喜欢新鲜的事物，它不希望有两天逛公园的路线完全一样，同时策策还是一个 特别热爱学习的好孩子，它不希望每天在逛公园这件事上花费太多的时间。如果1号点 到N号点的最短路长为d，那么策策只会喜欢长度不超过d + K的路线。

策策同学想知道总共有多少条满足条件的路线，你能帮帮它吗？

为避免输出过大，答案对P取模。

如果有无穷多条合法的路线，请输出-1。

题解：

话说去年提高组的难度真心大.......

我们一层一层考虑这道题：

1.首先，我们发现 $k<=50$，这个规模是非常小的。

2.由发现一，我们不难列出 dp 状态：$dp[i][j]$ 代表第 $i$ 号点到终点的距离比最短路大 $j$ 的方案数。

对于2的实现，我们考虑将每条边反着连

从N 点开始跑一遍到 1 号点的最短路，求出每个点到 N 号点的最短路。

我们这么做的原因是由于正着做可能会碰到不合法的状态，而逆推则不会碰到非法状态。

因为显然，1 号点的最短路径一定是全局的最短路径，于是可以由 1 号点转移的状态就全部是合法的，依此类推。

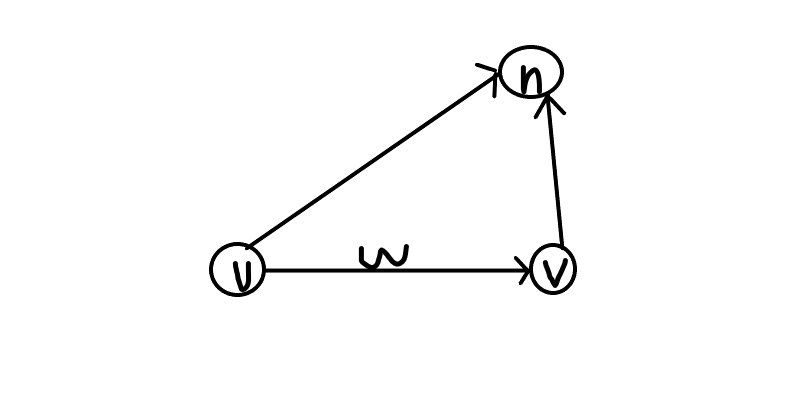
考虑正着进行记忆化搜索，从一个点转移到另一个点时，所需要走的最短路径为 $d[v]+w$。

而原本的最短路径为 $d[u]$，那么这就比 $d[u]$ 多了 $d[v]+w-d[u]$ 的路程。

假设当前的偏移量（即比最短路多出的量）为 $k$。

那么转移到 $v$ 点之后的偏移量就会变成 $k-(d[v]+w-d[u])$

我们这么进行记忆化搜索即可。

不过我们还要判一下 0 环。 开一个 $vis[i][k]$ 数组即可。

发现该状态再一次被访问且 $vis[i][k]=true$ 就说明出现 0 环，直接输出 -1.

Code:

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<string>
using namespace std;
const int maxn=400000+4;
int d[maxn],s, n ,m, mod,tot;
struct SPFA{
	int head[maxn],to[maxn],nex[maxn],val[maxn],cnt;
	void addedge(int u,int v,int c){
		nex[++cnt]=head[u],head[u]=cnt,to[cnt]=v,val[cnt]=c;
	}
	queue<int>Q;
	bool inq[maxn];
	void init(){
		memset(head,0,sizeof(head)), memset(to,0,sizeof(to)), memset(nex,0,sizeof(nex)), memset(val,0,sizeof(val));
		cnt=0;
	}
	void spfa(){
		memset(d,0x3f,sizeof(d));
		memset(inq,false,sizeof(inq));
		d[s]=0,inq[s]=true; Q.push(s);
		while(!Q.empty()){
			int u=Q.front();Q.pop(); inq[u]=false;
			for(int v=head[u];v;v=nex[v]){
				if(d[u]+val[v]<d[to[v]]){
					d[to[v]]=d[u]+val[v];
					if(!inq[to[v]]){ Q.push(to[v]); inq[to[v]]=true; }
				}
			}
		}
	}
}T;
int head[maxn], to[maxn], nex[maxn], val[maxn], cnt;
void addedge(int u,int v,int c){
	nex[++cnt]=head[u], head[u]=cnt, to[cnt]=v, val[cnt]=c;
}
int dp[100007][60];
bool vis[100007][60];
int dfs(int u,int k){
	if(vis[u][k]) return -1;
	if(dp[u][k]!=-1) return dp[u][k];
	vis[u][k]=1;
	int sum=0;
	for(int v=head[u];v;v=nex[v]){
		int tmp=k-(d[to[v]]+val[v]-d[u]);
		if(tmp<0||tmp>tot) continue;
		int delta=dfs(to[v], tmp);
		if(delta==-1) return -1;
		sum=(sum+delta)%mod;
	}
	if(k==0&&u==n) sum+=1;
	vis[u][k]=0;
	dp[u][k]=sum;
	return sum;
}
int work(){
	memset(dp,-1,sizeof(dp));
	memset(head,0,sizeof(head));
	memset(to,0,sizeof(to));
	memset(val,0,sizeof(val));
	cnt=0;
	T.init();
	scanf("%d%d%d%d",&n,&m,&tot,&mod);
	for(int i=1;i<=m;++i){
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		T.addedge(b,a,c);                         // 返向
		addedge(a,b,c);                           // 正向
	}
	s=n;
	T.spfa();
	int ans=0;
	for(int i=0;i<=tot;++i){
		memset(vis,0,sizeof(vis));
		int aa=dfs(1,i);
		if(aa==-1) return -1;
		ans=(ans+aa)%mod;
	}
	return ans;
}
int main(){
	int T;
	scanf("%d",&T);
	while(T--) printf("%d\n",work());
	return 0;
}